Классификация и идентификация эллипсовидных овальных кривых

Виктор Чебыкин

Введение

Продолжая рассмотрение эллипсовидных овальных кривых (Э.О.К.), начатое в статьях [1], [2] и [3], остановимся еще на трех: циклоидальный овал; гиперэллипс Ламе; овальная кривая Rr — овал по сопрягаемым дугам окружностей (рис. 1). При этом также попробуем классифицировать их и другие Э.О.К. на три группы: гиперовалы, гипоовалы и гипергипоовалы. В последнем разделе речь идет об идентификации Э.О.К. 

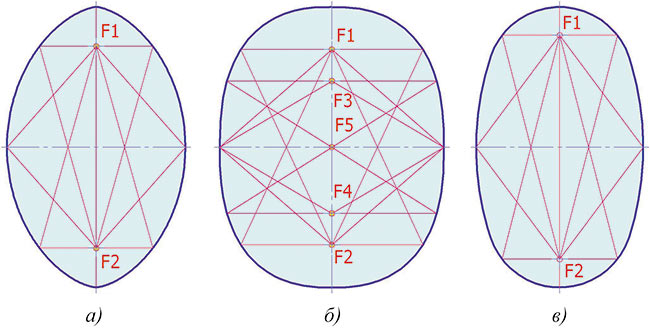
Рис. 1. Овальные кривые: а — циклоидальный овал; б — гиперэллипс Ламе;
в — овальная кривая Rr (гиперовал)

Циклоидальный овал

Циклоидальный овал (рис. 1а и 2) — это плоская гладкая замкнутая эллипсовидная двухфокусная овальная кривая, полученная в результате зеркальной стыковки двух «арок» циклоиды. Циклоида — плоская трансцендентная кривая; это траектория точки окружности, катящейся по прямой линии [4].

Одним из свойств циклоидального овала является наличие двух фокусов, имеющих строго определенное расположение.

Фокусы могут обменяться между собой восемью парами лучей, отраженных от кривой, и парой прямых лучей. Это свойство совпадает с аналогичным у кривой R­1, описанной в [3]. Точки падения этих лучей на кривую, так же как у кривой R­1, являются характерными — в них меняется знак роста суммы пары отрезков от точки кривой до фокусов на противоположный.

Еще одно свойство циклоидального овала: размеры некоторых элементов овала могут быть вычислены как произведение радиуса производящей окружности данной циклоиды или размеров полуосей с определенными константами. О последних и пойдет речь далее.

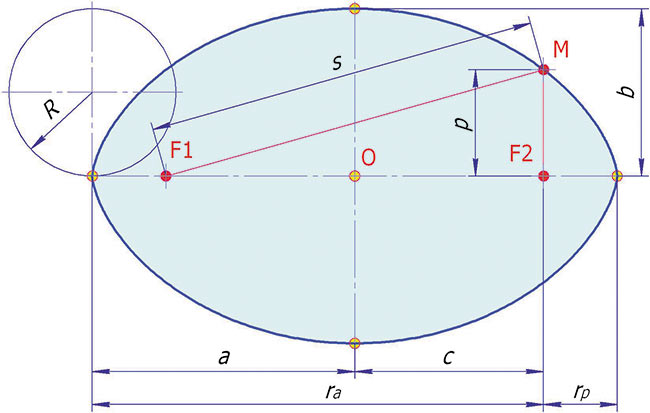
Рис. 2. Циклоидальный овал

Элементы овала (рис. 2):

• R — радиус производящей окружности цик­лоиды;
• a — большая полуось;
• b — малая полуось;
• с — фокальный радиус (полурасстояние между фокусами);
• p — малый фокальный луч;
• s — большой фокальный луч;
• rp — перифокусное расстояние (минимальное расстояние от фокуса до точки на овале);
• ra — апофокусное расстояние (максимальное расстояние от фокуса до точки на овале).

Константы циклоидального овала:

1. Константа соотношения осей овала
   Ксо1 = а/b = p/2;
2. Фокальная константа
   Vco = c/R ≈ 2,259 360 664 54…;
3. Перифокусная константа
   PVco = rp/R ≈ 0,882 231 989 04…;
4. Апофокусная константа
   AVco = ra/R ≈ 5,400 953 318 13…;
5. Эксцентриситет­константа
   Eco = с/a ≈ 0,719 176 835 98…;
6. Константа малого фокального луча
   Lco = p/R ≈ 1,270 684 347 65…;
7. Константа большого фокального луча
   GLco = s/R ≈ 4,693 983 506 71…

Попытка найти в литературе и Интернете сведения по константам циклоидальных овалов ничем не увенчалась, поэтому названия констант и их обозначения автор предложил свои. Ну и значения констант, за исключением первой, пришлось определить самому.

Теперь отнесем этот овал к одной из групп: гиперовалы (от греч., гипер —  «над, выше»); гипоовалы (гипо — «под, ниже»); гипергипоовалы.

Построим по полюсам данного овала эллипс и увидим, что он будет описанным по отношению к овалу, а овал соответственно — вписанным в эллипс. Исходя из этого, циклоидальный овал является гипоовалом. Циклоидальные кривые используются в технике: маятник Гюйгенса; кривая кратчайшего спуска; циклоидальные передачи и редукторы; кулачки и эксцентрики…

Гиперэллипс Ламе

Кривая показана на рис. 1б. Такую форму и такое название кривая имеет, если степени m и n в формуле кривой Ламе больше 2.

Гиперэллипс, так же, как овал Кассини (который описан в [3]), имеет два основных оптических фокуса и три дополнительных. Само название его говорит о том, к какой группе следует отнести этот овал — к гиперовалам.

Рис. 3. Разновидности овальных кривых Rr

Гипоэллипс Ламе, показанный в [3], где он был назван просто кривой Ламе, в формуле имеет степени m и n меньше 2. При степенях m и n равных 2 кривая Ламе является эллипсом. В случае если одна из степеней больше, а другая меньше 2, мы имеем гипергипоэллипс (рисунок не показан). Если по полюсам этого овала построить эллипс, то можно увидеть, что кривые имеют как точки касания, так и точки пересечения между собой.

Овальная кривая Rr

Овальная кривая Rr — овал по сопрягаемым дугам окружностей (рис. 1в и 3). Эти овалы хорошо известны тем, кто учился в докомпьютерную эру (по аналогии с «до н.э.» имеем «до к.э.»). Ими пользовались для упрощенного изображения эллипсов на чертежах. Сейчас, по понятным причинам, необходимость в этом отпала. В технике эти овалы все же используются — кулачки, эксцентрики и т.п.

На рис. 1в изображена овальная кривая Rr (гиперовал), а на рис. 3  —сразу три вида овалов: внутренний — гиперовал; наружный — гипоовал; средний — гипергипоовал. Тонкими линиями показаны соответствующие этим овалам эллипсы, которые помогают определить принадлежность кривых к той или иной группе.

Классификация кривых, описанных в статье [3]:

• овал Кассини — гиперовал;
• кривая Ламе (показанная) — гипоовал;
• кривые R­0 и R­1 — гипоовалы;
• кривая R­2: верхняя часть — гиперовал, нижняя — гипоовал.

Идентификация эллипсовидных овальных кривых

Итак, для идентификации предлагаются следующие кривые: эллипс, овал Кассини, гиперэллипс Ламе; гипоэллипс Ламе; гипергипоэллипс Ламе; овал R­0; овал R­1; циклоидальный овал; гиперовал Rr; гипоовал Rr; гипергипоовал Rr. Зная геометрию и свойства данных кривых, классификацию можно выполнить визуально, однако иногда  некоторые из них бывают очень схожи.

Идентификацию лучше проводить в той CAD­программе, в которой эти кривые созданы. Автор для построения и идентификации кривых использовал  программу КОМПАС.

При поочередном входе в режим редактирования кривых можно сразу распознать эллипс и все овалы по сопрягаемым дугам окружностей, группу которых определяем сопряжением с эллипсом. Все остальные кривые при редактировании покажут, что построены с помощью кривой Безье.

Оставшиеся кривые сначала необходимо разбить на группы в соответствии с нашей классификацией путем сопряжения с соответствующими им эллипсами.

В группе гипергипоовалов окажется только гипергипоэллипс, так как гипергипоовал Rr распознан уже на первой стадии идентификации.

Далее рассмотрим группу гипоовалов. Поскольку гипоовал Rr также распознан на первой стадии, в ней остаются: кривая R­0; кривая R­1; гипоэллипс Ламе; циклоидальный овал. Последний распознаем с помощью эксцентриситет­константы циклоидального овала (пригодилась!). Для этого поочередно для каждой кривой рассчитываем фокальный радиус, умножая размер большой полуоси на эксцентриситет­константу Eco. Тот овал, в котором пучок из восьми лучей, выпущенных из фокуса и отраженных от кривой, соберется в противоположном фокусе, и будет циклоидальным овалом. Для распознавания оставшихся трех гипоовалов рассмотрим три возможных сценария идентификации. Все зависит от количества фокусов у гипоэллипса Ламе. Первый вариант — кривая Ламе имеет четыре фокуса (например, при сочетании параметров: a/b = 7/10; n = m = 1,7). В этом случае удается распознать все кривые: бесфокусную R­0, двухфокусную R­1 и четырехфокусную  кривую Ламе.  Второй вариант — кривая Ламе бесфокусная (например, при сочетании параметров: a/b = 8/10; n = m = 1,7). При этом сможем распознать только R­1. Кривая R­0 и гипоэллипс будут трудноразличимыми. Третий вариант — кривая Ламе имеет два фокуса (например, при сочетании параметров: a/b = 8/10; n = 1,7 и m=1,9). Выявить при этом удастся  только кривую R­0. Различить R­1 и гипоэллипс Ламе можно по форме кривых и расположению фокусов… 

Осталось разобраться с гиперовалами. После первой стадии идентификации, где был определен гиперовал Rr, их у нас осталось два: овал Кассини и гиперэллипс Ламе. Для идентификации их в первую очередь необходимо выровнять масштабированием размеров овалов по высоте. Далее нужно определить положение фокусов (тех, которые фигурируют в определении овала Кассини) относительно центра и нанести их. Оптические фокусы овалов использовать нельзя — у них другие координаты. Та кривая, на которой будет соблюдено следующее условие: произведение расстояний от любой точки кривой до фокусов есть величина постоянная, — и есть овал Кассини. Если степени гиперэллипса Ламе равны 2,5 и более, то кривые хорошо различимы визуально — кривая Ламе более угловатая.

Выводов делать не будем. Главное, что почти все точки над «о» расставлены. 

Библиографический список

1. Чебыкин В.Г. Врезка люков в обечайки резервуаров, соединения с минимальными (гарантированными) зазорами. Новые виды овальных кривых — «резервуарные» овалы. Справочник // Инженерный журнал. 2012. № 11. С. 31­33.
2. Чебыкин В.Г. Особенности технологии врезки люков и патрубков в обечайки резервуаров // Технология машиностроения. 2013. № 1. С. 33­35.
3. Чебыкин В. А не замахнуться ли нам на Габриеля нашего Ламе? // САПР и графика. 2013. № 8. С. 92, 94­95.
4. Математическая энциклопедия (в 5 томах). М.: Советская энциклопедия, 1982. Т.5. С. 809.

САПР и графика 3`2014