Использование CAE-системы FlowVision для исследования взаимодействия потоков жидкости в центробежно-струйной форсунке

Елена Туманова

Постановка задачи

Результаты численного эксперимента

В данной работе численное исследование проводилось с использованием программного комплекса FlowVision, который предназначен для моделирования трехмерных течений жидкости и газа в технических и природных объектах, а также для визуализации этих течений методами компьютерной графики. С помощью указанного программного комплекса в работе решалась задача моделирования взаимодействия потоков жидкости внутри центробежно-струйной форсунки с тангенциальным вводом периферийного потока.

Эскиз конструкции форсунки, для которой были проведены испытания, представлен на рис. 1. Следует отметить, что прототипами исследованной форсунки являются форсунка ВТИ и форсунка по авторскому свидетельству № 1118420. Характерные размеры форсунки были следующие: диаметр соплового отверстия — 4 мм, диаметр тангенциальных и осевого каналов — 3 мм , внутренний радиус камеры смешения — 8 мм, высота зоны взаимодействия потоков изменялась от 6 до 16 мм.

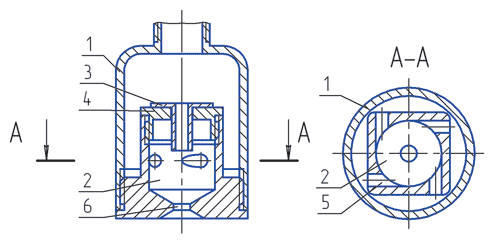
Рис. 1. Эскиз центробежно-струйной форсунки: 1 — корпус форсунки; 2 — камера смешения; 3 — втулка осевого канала; 4 — крышка камеры смешения; 5 — тангенциальный канал; 6 — сопловое отверстие

Постановка задачи

Первоначально была создана твердотельная модель внутреннего пространства форсунки, файл которой далее импортировался в комплекс FlowVision. Геометрия расчетной области представляет собой объем, в котором определены уравнения математической модели. Поверхность расчетной области представляют собой совокупность плоских многоугольников — фасеток, на которых определены граничные условия.

При исследовании гидродинамических характеристик форсунки интерес представляет взаимодействие потоков внутри камеры смешения и в сопловом отверстии. Поэтому после численного расчета полной форсунки, для некоторого упрощения задачи, твердотельная модель была сокращена и не содержала пространство вне камеры смешения. Данное упрощение не искажает конечного результата, поскольку геометрия камеры смешения не изменена. Численный расчет полной форсунки позволил нам оценить соотношение скоростей жидкости в осевом и тангенциальных каналах. В тангенциальных каналах скорость жидкости несколько меньше, чем в осевом, вследствие гидравлических потерь напора из-за необходимости периферийного потока менять направление движения. Полученная модель исследуемой внутренней области камеры смешения центробежно-струйной форсунки показана на рис. 2.

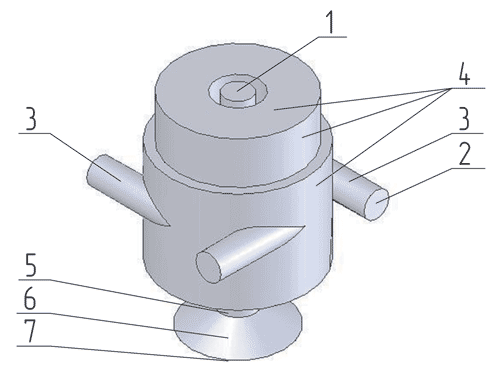
Рис. 2. Геометрия расчетной области: 1 — входное отверстие для осевого потока жидкости; 2 — входное отверстие для периферийного потока жидкости; 3 — стенка тангенциального канала; 4 — стенка камеры смешения форсунки; 5 — стенка соплового канала; 6 — расточка соплового канала на выходе из форсунки; 7 — выходное отверстие форсунки

В постановке задачи использовались следующие граничные условия:

1. Стенка с логарифмическим законом изменения скорости в турбулентном пограничном слое.

2. На входе задавалась нормальная скорость потока.

3. Выход свободный с нулевым давлением на границе.

В данной модели граничное условие «вход» было задано на пяти поверхностях, соответствующих поперечным сечениям четырех тангенциальных отверстий и одного осевого отверстия. Скорость жидкости на входе осевого канала была принята 6,5 м/с, на входе тангенциальных каналов — 5 м/с. Граничное условие «свободный выход» использовалось для поверхности, соответствующей поперечному сечению соплового отверстия форсунки; применялось условие «давление, без втока жидкости».

Целью моделирования движения жидкости в расчетной области является получение распределений скорости и давления жидкости. Чтобы рассчитать эти параметры, необходимо задать физические законы их изменения, а именно математическую модель. В качестве последней в данной работе для решения задачи формирования внутри камеры смешения факела распыленной жидкости использовалась модель «несжимаемая жидкость», которая позволяет моделировать течение при больших числах Рейнольдса и малых изменениях плотности.

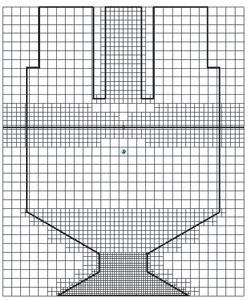
Для решения уравнений математической модели в работе применялась прямоугольная, адаптивная, локально измельченная конечно-объемная сетка. Схема сетки, использовавшейся для решения данной задачи, представлена на рис. 3.

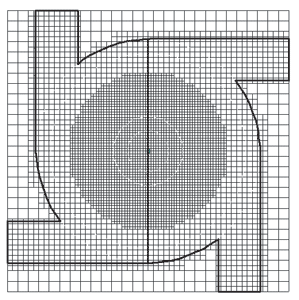ab

Рис. 3. Расчетная сетка: слева — вид сбоку; справа — вид сверху

Размеры одной ячейки начальной сетки составляют 0,74x0,72x0,74 мм. Адаптация 1-го уровня проведена по поверхностям: конусная поверхность камеры смешения на входе в сопловой канал, стенки осевого и тангенциальных каналов, входы осевого и периферийных потоков жидкости. Адаптация 2-го уровня проведена по следуюшим поверхностям: соответствующим сопловому каналу, расточке соплового канала и выходу жидкости из форсунки. Объемная адаптация 1-го уровня создана в зоне соплового канала и охватывает конусную поверхность камеры смешения и расточку. Объемная адаптация 2-го уровня охватывает сопловой канал.

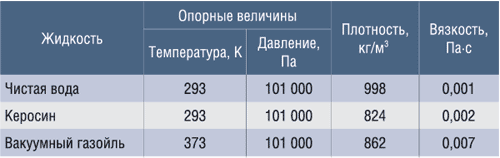
Жидкость для расчета была задана из базы данных FlowVision: чистая вода, керосин; кроме того, для расчета использовалась жидкость, внесенная в базу данных пользователем, — вакуумный газойль. Физические параметры жидкостей, использованных для расчета, а также опорные значения, при которых производилось моделирование, представлены в таблице. Опорная температура для вакуумного газойля, а также плотность и вязкость при этой температуре приняты по результатам работы модернизированной регулярными насадками колонны установки первичной переработки нефти.

Использовались параметры расчетного метода для определения скорости и давления, принятые по умолчанию для данной модели расчета.

Исследуемый геометрический параметр форсунки (высота поднятия втулки осевого канала h) для численного эксперимента задавался при построении твердотельной модели внутреннего пространства.

Численный расчет в данном программном комплексе не позволяет моделировать факел распыленной жидкости и оценить его дисперсность, поскольку в программе не заложен учет силы поверхностного натяжения жидкости и взаимодействия ее с окружающей средой. Поэтому результатом численного эксперимента являются полученные значения скорости и давления в любой точке внутренней полости, которые позволяют детально исследовать процесс взаимодействия потоков, выбрать оптимальное соотношение размеров форсунки и определить диапазон ее работы, что необходимо для обеспечения равномерного орошения поверхности жидкостью форсунками простой и надежной конструкции.

Для определения параметров распыленного факела рассчитанной модели необходимо выделить следующие результаты численного эксперимента: распределения полной скорости жидкости, а также ее осевого и тангенциальных компонентов в сопловом отверстии форсунки. Эти данные позволят судить о формирующемся факеле распыла и оценить плотность орошения данной форсункой.

Результаты численного эксперимента

В результате численного эксперимента получены распределения скоростей и давления жидкости во всех точках расчетного пространства, что позволило оценить эффективность конструкции.

На рис. 4 представлено распределение полной скорости в продольном и поперечном сечении камеры смешения форсунки. Распределение скорости представлено в виде заливки по значениям. Поперечное сечение проходит через центр тангенциальных каналов.

На рис. 5 показано распределение осевой и тангенциальной скорости в продольном сечении камеры смешения форсунки.

На рис. 6 изображено распределение полного давления в продольном и поперечном сечении камеры смешения форсунки.

Из рис. 4 видно, что тангенциальные потоки, входя в камеру смешения, вначале не взаимодействуют с осевой струей. Осевой поток, проходя примерно до середины камеры смешения, перемешивается своими периферийными слоями с жидкостью, заполняющей камеру смешения. В результате этого снижается скорость периферийных слоев осевого потока (рис. 4а и 5а). Взаимодействие осевого и вращающегося потоков начинается на входе в сужающуюся часть камеры смешения перед сопловым отверстием.

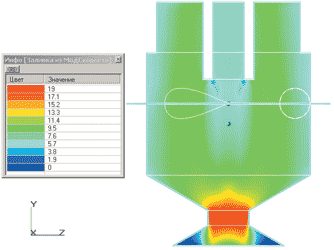
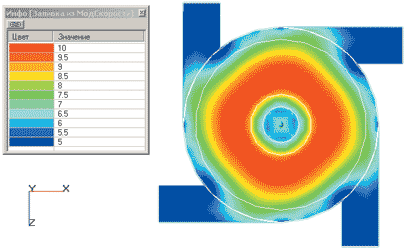
Рис. 4. Распределение полной скорости (м/с) внутри камеры смешения центробежно-струйной форсунки: слева — в продольном сечении; справа — в поперечном

Из рис. 5б видно, что в сопловом отверстии форсунки тангенциальный компонент скорости возрастает от центра к периферии. В центре соплового канала тангенциальный компонент скорости равен нулю. Это соответствует тому, что в сопловом канале взаимодействуют осевой и вращающийся потоки, тогда как полная скорость жидкости в сопловом канале постоянна по всему поперечному сечению (рис. 4а).

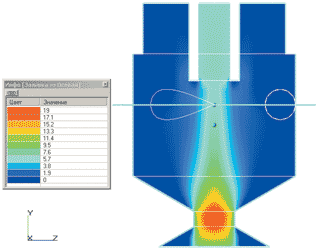
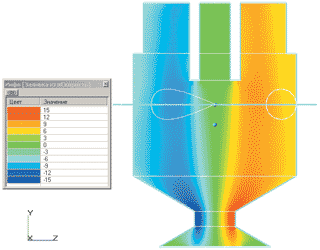
Рис. 5. Распределение осевого и тангенциального компонентов скорости (м/с) внутри камеры смешения центробежно-струйной форсунки: слева — осевой компонент скорости; справа — тангенциальный

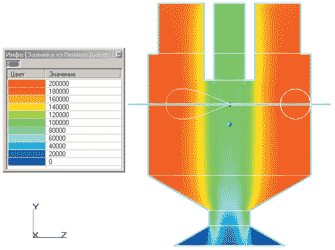
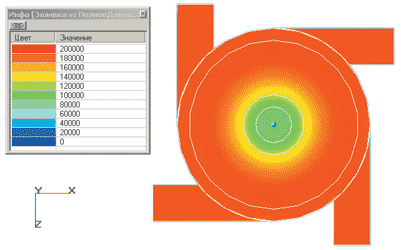
Рис. 6. Распределение полного давления (Па) внутри камеры смешения центробежно-струйной форсунки: слева — в продольном сечении; справа — в поперечном

Следует отметить, что полное давление в данном программном комплексе складывается из избыточного и динамического, без учета атмосферного. Атмосферное давление задано в опорных величинах, поэтому ноль на шкале давлений (рис. 6) соответствует 101 000 Па. Из рис. 6 следует, что полное давление жидкости в камере смешения возрастает к периферии. На выходе из камеры смешения давление падает до атмосферного.

Параметры жидкостей, использованных для численного эксперимента

Из рис. 4 и 5 видно, что распределение скоростей имеет окружную равномерность, поэтому рассмотрим распределение осевого, тангенциального компонентов и полной скорости в виде графиков вдоль радиуса, лежащего в плоскости соплового отверстия.

Распределение скоростей для численного эксперимента на воде представлено на рис. 7, из которого видно, что полная скорость сохраняет постоянное значение практически по всему поперечному сечению соплового отверстия, тогда как осевая скорость убывает от центра к периферии, а тангенциальная, наоборот, возрастает, что согласуется с литературными данными и говорит о взаимодействии в сопловом канале форсунки двух потоков — поступательного и вращательного. На данном рисунке не просматривается принципиальное различие в распределении скоростей при изменении высоты камеры смешения.

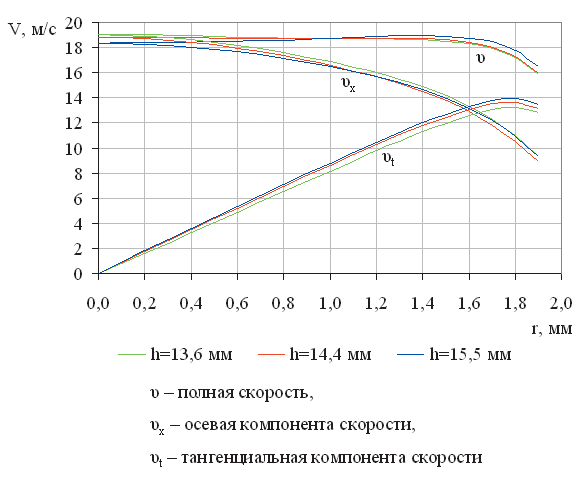
Рис. 7. Графики полной скорости и ее компонентов вдоль радиуса соплового отверстия для воды

Для того чтобы различия были нагляднее, представим распределение полной скорости с более подробной шкалой. На рис. 8 четко видны различия в распределении полной скорости по поперечному сечению соплового отверстия при изменении высоты камеры смешения.

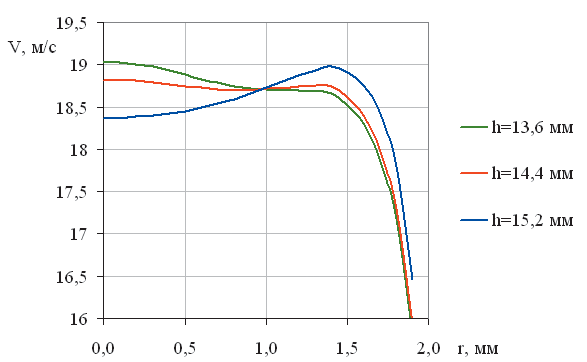
Рис. 8. Графики полной скорости вдоль радиуса соплового отверстия для воды

По результатам численного расчета форсунки с использованием керосина также были построены графики распределения скорости и ее компонентов вдоль радиуса соплового отверстия, которые представлены на рис. 9. Графики полной скорости с более подробной шкалой ординат показаны на рис. 10.

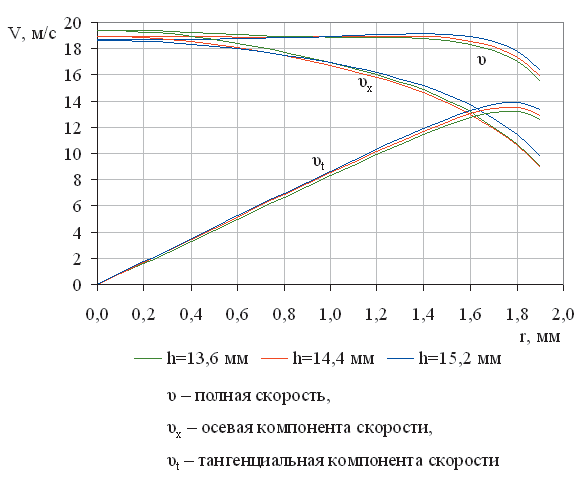
Рис. 9. Графики полной скорости и ее компонентов вдоль радиуса соплового отверстия для керосина

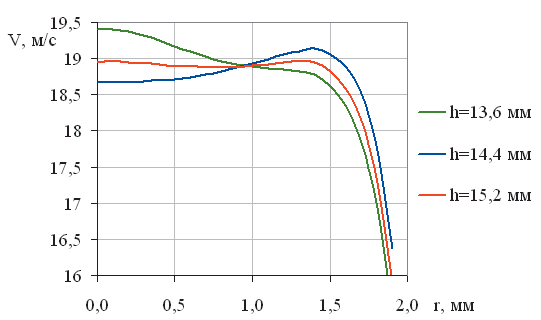
Рис. 10. Графики полной скорости вдоль радиуса соплового отверстия для керосина

Из рис. 9 и 10 следует, что изменение жидкости, а именно изменение вязкости жидкости в 2 раза, не очень повлияло на распределение скоростей в сопловом канале форсунки. Однако численный расчет с использованием жидкости «вакуумный газойль» показал, что вязкость все же оказывает влияние на взаимодействие потоков и с ее увеличением оптимальная высота камеры смешения возрастает.

На рис. 11, где представлены графики полной скорости вдоль радиуса соплового отверстия для жидкости «вакуумный газойль» видно, что для жидкости «вакуумный газойль» оптимальная высота камеры смешения составляет 16,0 мм . Следует отметить, что вязкость вакуумного газойля в 7 раз больше вязкости воды, а оптимальная высота камеры смешения при этом увеличилась всего на 11%.

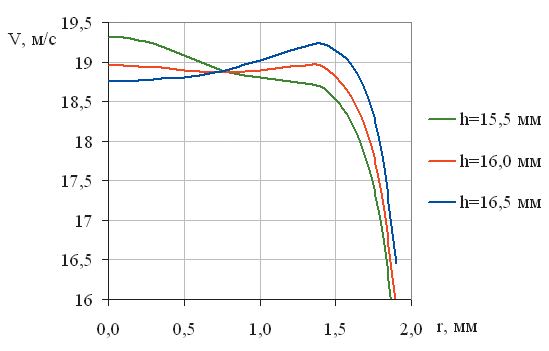
Рис. 11. Графики полной скорости вдоль радиуса соплового отверстия для вакуумного газойля

Характер графиков полной скорости вдоль радиуса соплового отверстия повторяет вид графиков распределения плотности орошения вдоль радиуса орошенной поверхности. Последние получены в результате натурных экспериментов для центробежно-струйной форсунки с тангенциальным вводом периферийного потока. Натурные эксперименты проводились на форсунке, эскиз которой приведен на рис. 1. При проведении натурных экспериментов изменялся геометрический параметр — высота зоны взаимодействия потоков — путем поднятия и опускания втулки осевого канала. Натурный эксперимент был проведен на жидкости «вода» при перепаде давления жидкости на форсунке 300 кПа и расходе жидкости 1,7·10^-4м³/с. В результате натурного эксперимента получены графики плотности орошения, которые представлены на рис. 12.

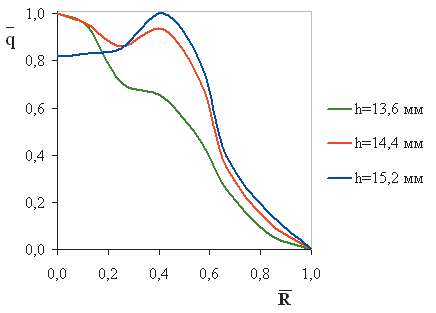
Рис. 12. Экспериментальные графики плотности орошения вдоль радиуса орошенной поверхности в относительных значениях

При использовании разработанной автором методики расчета плотности орошения форсунками, исследованными численно, были получены расчетные графики плотности орошения. При расчете плотности орошения исходными данными являются графики полной скорости и ее скорости вдоль радиуса соплового отверстия (см. рис. 7). Методика расчета плотности орошения основана на расчете траекторий капель с учетом изменения силы сопротивления, действующей на капли со стороны газового потока. Расчетные графики плотности орошения представлены на рис. 13. Плотность орошения приведена в относительных значениях для удобства сравнения результатов с натурным экспериментом.

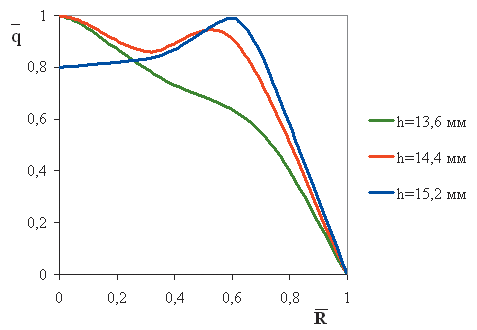
Рис. 13. Графики расчетной плотности орошения для воды

Из рис. 12 и 13 видно, что характер распределения расчетной плотности орошения согласуется с экспериментальными данными. Это подтверждает правильность как постановки численного эксперимента, так и методики расчета плотности орошения.

САПР и графика 9`2005