Проектирование шин с использованием программного комплекса ABAQUS
Осесимметричные задачи: посадка на диск и наддув шины
Трехмерный анализ статического пятна контакта
Анализ задачи постоянного качения шины
Импорт результатов и нестационарное вращение шины
Возможности моделирования протектора шины
Подход к расчету износостойкости шины
При проектировании современных шин для автомобильной промышленности необходимо рассматривать множество факторов нагружения, включая квазистатику, установившуюся динамику и нелинейные переходные процессы. Сложность конструкции типичных моделей автошин требует использования современных методов расчета. И здесь самым эффективным средством получения надежных результатов является конечно-элементный программный комплекс ABAQUS (www.abaqus.com).
Пакет ABAQUS — стандарт в области создания, проектирования и подготовки производства автомобильных шин. Он используется в таких компаниях-производителях, как Goodyear, Pirelli, Cooper, Yokohama, Hankook и др. ABAQUS имеет модульную структуру: два основных модуля решателей (солверов) — ABAQUS/Standard и ABAQUS/Explicit, препостроцессор ABAQUS/CAE и дополнительные модули, учитывающие особенности специфических проблем — ABAQUS/Aqua, ABAQUS/Design, ABAQUS/Safe. Все указанные модули органично дополняют друг друга.
Модуль ABAQUS/Standard, который построен на неявном методе решения, используется для задач посадки на диск, наддува шины и статического нагружения при контакте с дорогой. Возможности ABAQUS/Standard обеспечивают эффективный подход к решению задачи о постоянном качении шины, так как вычислительные затраты не зависят от скорости вращения шины. Благодаря этому ABAQUS/Standard может моделировать качение шины и на плоской дороге, и на тестовом стенде.
Неблагоприятные условия на дороге моделируются с использованием нестационарных динамических нагрузок. Модуль ABAQUS/Explicit применяется для таких задач, как столкновение с преградами, преодоление ям и бугров на дороге, влияние торможения или ускорения автомобиля и т.д. Кроме того, решение статических задач анализа, полученное в ABAQUS/Standard, можно использовать как начальное условие для анализа ABAQUS/Explicit, что значительно сокращает время расчета при комплексном нагружении.
Компания «ТЕСИС» не один год работает с ведущими российскими и западными производителями автомобильных шин. Помимо методики анализа прочности и динамики шин и резинокордных изделий техническими специалистами нашей компании разработан и реализован уникальный подход к анализу аквапланирования автомобильной шины и создана методика расчета акустического поведения шины.
Основные особенности ABAQUS
Одной из важнейших особенностей пакета ABAQUS является его универсальность: он может использоваться на всех этапах проектирования и создания современных изделий и практически всеми расчетными, проектными и технологическими службами предприятия.
Пакет ABAQUS тесно интегрирован почти со всеми CAD-системами (Unigraphics, Pro/ENGINEER, Catia , SolidWorks и др.), имеет современный и мощный препостпроцессор ABAQUS/CAE. Следует также отметить наличие связи через интерфейсы с другими программными продуктами: ADAMS (кинематика и динамика узлов и механизмов), SYSNOISE (акустика и виброакустика), Moldflow (литье пластмасс), FlowVision (аэро- и гидродинамика).
Из главных характеристик ABAQUS в области проектирования шин можно отметить следующие:
• широкий выбор гиперэластичных моделей состояния для резиновых материалов, используемых в шине;
• возможность точного моделирования шнуров подкрепления шины с учетом предварительного нагружения; при этом ABAQUS позволяет определять подкрепления независимо от геометрии шины, что значительно сокращает затраты при построении сетки для подкреплений;
• возможность переноса геометрии и результатов анализа от осесимметричной модели (используемой в анализе задач посадки на диск, наддува шины) к трехмерной модели (применяемой в задаче статического нагружения при контакте с дорогой, задаче постоянного качения и переходных задачах динамики);
• эффективное вычисление реакции в задаче постоянного качения шины для заданной скорости, используя смешанный подход Эйлера-Лагранжа в ABAQUS/Standard;
• импорт информации о расчетной модели и результатов анализа после окончания анализа задачи постоянного качения в ABAQUS/Explicit в качестве начальных условий при решении переходных задач динамики;
• моделирование нестационарных динамических процессов для больших моделей с помощью ABAQUS/Explicit.
Выбор моделей расчетов
Расчет автошины является очень трудным делом из-за сложной геометрии, повышенных требований к моделированию вследствие наличия всевозможных типов нагружения — от квазистатических до нестационарных динамических задач, а также с учетом общих условий контакта.
Моделирование автошин требует применения гиперэластичных моделей материалов для резиновых компонентов и точного учета расположения и свойств подкреплений. В ABAQUS пользователи имеют возможность задавать потенциал энергии напряжения гиперэластичного материала, используя хорошо известные математические модели материалов либо вводя результаты экспериментальных данных напрямую.
Определение свойств подкрепляющих кордов упрощается вследствие введения допущения о том, что геометрия подкрепления рассматривается независимо от материала, окружающего подкрепление. Построение сетки для кордов, таким образом, строится независимо от слоев резиновых компонентов шины. Для этой цели ABAQUS вводит поверхностные элементы, которые могут описать свойства подкреплений. Поверхностные элементы не имеют никаких конструкционных свойств и используются только для того, чтобы определить геометрию кордов. Такие элементы врезаны в трехмерные элементы типа солид, применяемые для моделирования резиновых компонентов шины. При этом вводятся ограничения между узлами сетки матрицы материала резины и узлами поверхностных элементов подкреплений. Использование врезанных элементов позволяет предотвратить такие трудности построения сетки для подкреплений, как наличие очень малых элементов между слоями подкреплений.
Анализ нестационарного качения может быть рассмотрен как последовательность шагов нагружения; при этом каждый следующий шаг нагружения требует завершения предыдущего шага. Первым этапом нагружения является задача посадки на диск, второй этап — наддув шины, третий — нагружение шины весом автомобиля с учетом контакта с дорогой для определения статического пятна контакта. Четвертый этап определяет поведение автошины при качении с постоянной скоростью, при этом можно получать результаты для усилий и моментов на шпинделе. Результаты задачи постоянного качения могут быть использованы как начальные условия для пятого этапа, на котором проводится анализ нестационарного качения. На всех этапах расчета пользователь получает полную информацию о состоянии шины. На рис. 1 представлена блок-схема комплексного подхода к анализу поведения шин в ABAQUS.
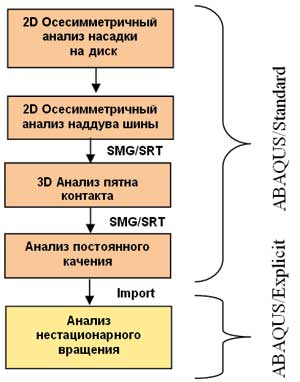
Рис. 1. Блок-схема комплексного подхода ABAQUS к анализу поведения шин (SMG — Symmetric Model Generation, SRT — Symmetric Results Transfer)
По мере возможности используется симметрия конструкции для уменьшения размера расчетной модели и увеличения вычислительной эффективности. Так, в задачах посадки на диск и наддува применяется осесимметричная модель для половины шины. Возможность построения симметричной модели используется при построении частично трехмерной модели для анализа статического пятна контакта и полностью трехмерной модели для задач постоянного и нестационарного качения.
Задачи посадки на диск, наддува и определения статического пятна контакта являются квазистатическими, вследствие чего они могут быть эффективно решены с помощью неявного метода решения в ABAQUS/Standard. В задаче о постоянном качении шины используется смешанный подход Эйлера-Лагранжа в ABAQUS/Standard. Эта возможность позволяет получить решение без вычислительных затрат, связанных с процедурой получения решения в явном виде, причем данные затраты не зависят от скорости вращения. Результаты четвертого этапа применяются в качестве начальных условий для нестационарного качения шины, когда моделируется наезд шины на серию препятствий при определенной скорости вращения путем рассмотрения нелинейной нестационарной динамики в ABAQUS/Explicit.
Далее мы более подробно рассмотрим этапы нагружения и представим вашему вниманию некоторые результаты расчетов.
Осесимметричные задачи: посадка на диск и наддув шины
Осесимметричный профиль шины применяется для анализа задач посадки шины на диск и наддува шины. На этой стадии рассматривается только половина поперечного сечения шины, как показано в рис. 2, а на срединной плоскости используются условия симметрии.
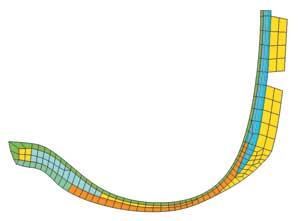
Рис. 2. Осесимметричная модель шины
Для модели со слоями кордов применяются попарные слои с симметричной ориентацией в направлении движения, и если один слой пары ориентирован на угол q° по отношению к направлению перемещения, то другой слой пары ориентирован на угол – q°. Слои подкреплений проходят через толщину протектора, так как они не могут занимать один и тот же объем, вследствие чего вводится зависимость между объемной и плоской деформациями сдвига в конструкции. Поэтому в том случае, когда шина деформирована, происходит передача кручения или относительного вращения боковых стенок на шпиндель. Для моделирования указанного процесса вводятся специальные осесимметричные элементы, имеющие в качестве независимой степени свободы кручение в окружном направлении.
Подкрепление в виде корда полностью описывается поперечным сечением каждой нити, расстоянием между нитями, свойствами материалов нитей и их ориентацией. На рис. 3 и 4 приведены трехмерный и двумерный виды такого подкрепления.
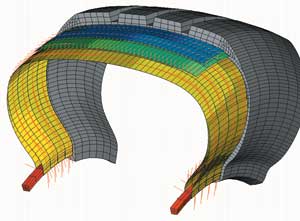
Рис. 3. Ориентация подкреплений в брекерах и каркасе — 3D-модель
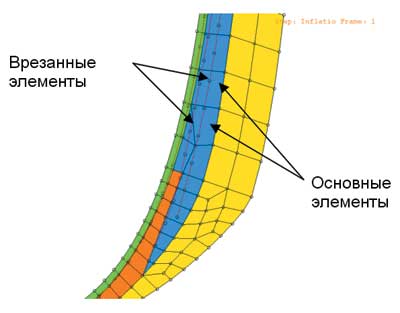
Рис. 4. Врезанные элементы в поперечном сечении — 2D-модель
Диск обычно представляется как твердая поверхность, что приводит к упрощению анализа, при этом моделируется контакт между диском и шиной с учетом трения. Диск может находиться в заданном положении относительно шины перед приложением давления наддува.
Трехмерный анализ статического пятна контакта
Нагрузка во время этого этапа анализа не является осесимметричной, вследствие чего требуется рассмотрение трехмерной модели. Симметричная генерация модели (Symmetric Model Generation, SMG) использована для того, чтобы создать начальную модель путем вращения профиля поперечного сечения вокруг оси. Ось вращения параллельна оси вращения шины.
Поскольку окончательная модель должна описывать нестационарный динамический анализ вращения шины в постановке Лагранжа, вокруг окружности используется достаточно равномерная и подробная сетка. Результаты осесимметричного анализа передаются для вновь сгенерированной трехмерной модели посредством процедуры симметричного переноса результатов (Symmetric Results Transfer, SRT).
Анализ задачи статического пятна контакта выполнен на половинной симметричной трехмерной модели в целях сокращения времени вычислений (рис. 5). На срединной плоскости, перпендикулярной оси шпинделя шины, приложены антисимметричные условия. На следующем этапе расчета процедуру симметричной генерации модели можно использовать снова, для того чтобы произвести полностью трехмерную модель. Результаты анализа задачи о пятне контакта могут быть перенесены в трехмерную модель посредством процедуры симметричного переноса результатов.

Рис. 5. 3D-модель (показана частично), построенная с использованием процедуры симметричной генерации модели
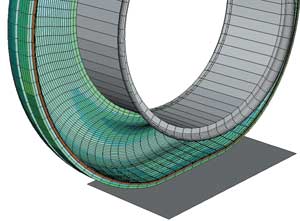
Рис. 6. 3D-модель (показана частично) для решения задачи определения пятна контакта
В процессе анализа дорога представляется как твердая поверхность, при этом моделируется контакт между шиной и дорогой. На рис. 6 частично представлена деформированная трехмерная модель, а на рис. 7 полностью показана деформированная трехмерная модель. Распределение давления в пятне контакта демонстрируется на рис. 8.
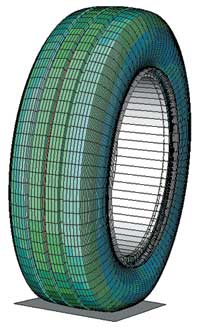
Рис. 7. 3D-модель (показана полностью), построенная с использованием процедуры симметричной генерации модели (SMG)
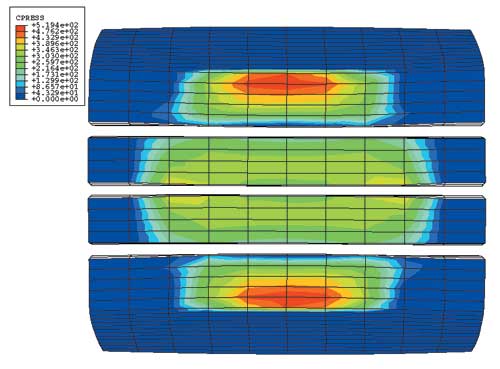
Рис. 8. Распределение контактного давления в задаче определения пятна контакта
Анализ задачи постоянного качения шины
Задача постоянного качения шины наиболее эффективно моделируется путем использования системы координат, связанной с осью шины. Система координат перемещается совместно с осью шины, но не вращается, в то время как шина вращается относительно данной системы координат. В этой системе координат наблюдатель видит шину как неподвижные точки, хотя материал, из которого сделана шина, движется через данные точки. Конечно-элементная сетка шины в этой системе координат остается неподвижной. Такое кинематическое описание можно рассматривать как смешанную формулировку Эйлера-Лагранжа, где вращение твердого тела описано с использованием подхода Эйлера, а деформация измеряется с помощью подхода Лагранжа.
Следует отметить, что подробная сетка необходима только вблизи зоны пятна контакта. Но если цель анализа заключается в вычислении реакции в задаче постоянного качения, то можно использовать специальные цилиндрические элементы, что значительно уменьшает размерность задачи.
Для задачи нестационарного качения шины применяется подход Лагранжа, который требует подробной сетки вокруг окружности для того, чтобы правильно описать условия контакта. До тех пор пока рассматривается только прямолинейное вращение, имеется возможность использования процедуры симметричного переноса результатов для анализа движения на повороте и подъеме.
Давление в пятне контакта и сдвигающие усилия представлены на рис. 9 и 10 соответственно, а на рис. 11 показано распределение усилия в брекерном слое.
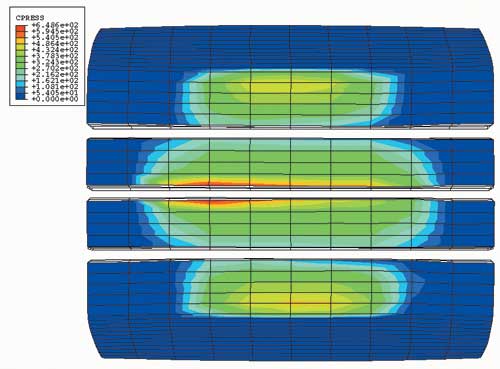
Рис. 9. Распределение контактного давления в задаче постоянного качения
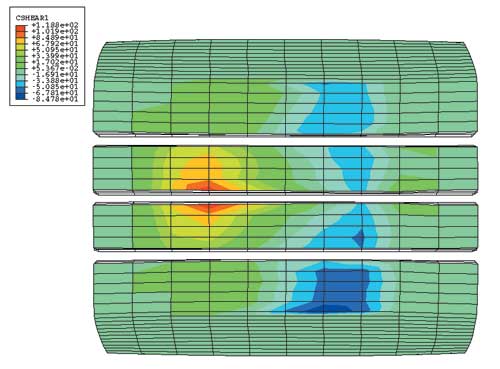
Рис. 10. Распределение сдвиговых усилий в направлении движения в задаче постоянного качения
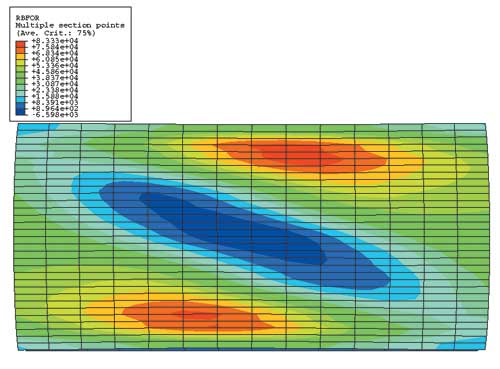
Рис. 11. Распределение усилий в брекере, ближнем к пятну контакта движения, в задаче постоянного качения
Импорт результатов и нестационарное вращение шины
Информацию о модели и результаты анализа можно перенести из ABAQUS/Standard в ABAQUS/Explicit и наоборот. Результаты анализа задачи постоянного качения в качестве начальных данных переносятся в ABAQUS/Explicit для анализа нестационарного вращения шины (рис. 12).

Рис. 12. 3D-модель, импортированная в ABAQUS/Explicit из ABAQUS/Standard
На рис. 12 показана первоначальная конфигурация модели, используемой для анализа нестационарного вращения шины. Дорога и диск представлены как твердые поверхности; коэффициенты трения между дорогой и шиной, а также между диском и шиной равны 1.0, высота препятствия составляет приблизительно 10% от радиуса шины.
В указанном случае шина движется с постоянной скоростью 60 км/ч вдоль направления движения (такая же скорость используется в задаче постоянного качения). Нагрузка от веса автомобиля приложена к референсному узлу твердой поверхности диска. Типичные результаты расчета, включая деформацию, давление контакта и усилия в подкреплении, представлены соответственно на рис. 13-15.

Рис. 13. Деформация шины при наезде на первое препятствие

Рис. 14. Распределение контактного давления при наезде на первое препятствие
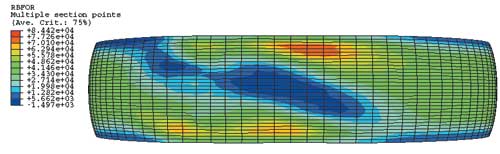
Рис. 15. Распределение усилий в брекере, ближнем к пятну контакта, при наезде на первое препятствие
Возможности моделирования протектора шины
В ABAQUS имеется множество уникальных возможностей для быстрого и удобного решения всей линейки задач с учетом реальной геометрии протектора. В частности, чтобы смоделировать весь протектор, достаточно построить одну периодическую его часть (рис. 16). Соединение протектора с шиной осуществляется посредством опции Tie Constraint.
Задачу посадки на диск теперь можно решать с учетом реальной геометрии протектора, взяв при этом лишь один периодический сектор (рис. 17).
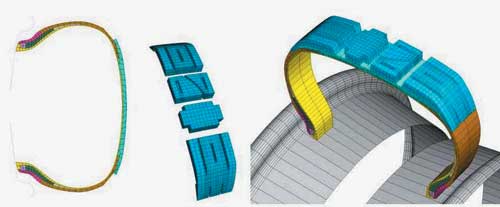
Рис. 16. Моделирование протектора посредством периодического сектора
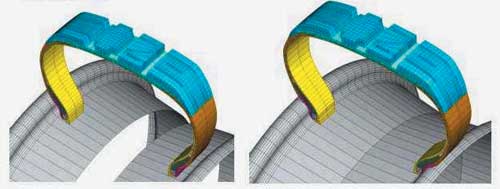
Рис. 17. Посадка на диск с реальной геометрией протектора
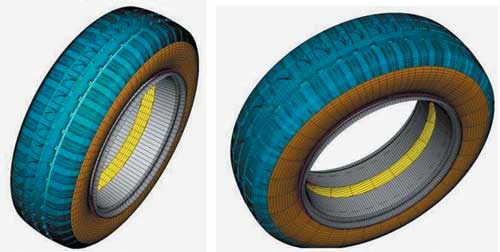
Рис. 18. Виды полного протектора с периодическими и с нерегулярными секторами
Полную модель с протектором можно создать с помощью опции Symmetric Model Generation (рис. 18). При этом есть возможность регулировать величину угла раствора каждого периодического сектора протектора в тех местах, где реальная геометрия протектора не имеет особого значения, но это помогает значительно уменьшить вычислительные затраты. В частности, это будет эффективно при решении задачи о пятне контакта.
Подход к расчету износостойкости шины
Существенной составляющей процесса проектирования шин является исследование их износостойкости. Пакет ABAQUS позволяет рассчитать износ шин при различных режимах движения и при разной величине пробега — для этого пользователь задает закон изменения износа материала шины и ALE-технологию (произвольный подход Лагранжа-Эйлера) при перестраивании сетки с помощью специальной подпрограммы UMESHMOTION.
На рис. 19 в качестве примера представлены сетки до и после износа шины, а на рис. 20 приведены результаты распределения контактного давления в пятне контакта для этих двух случаев.
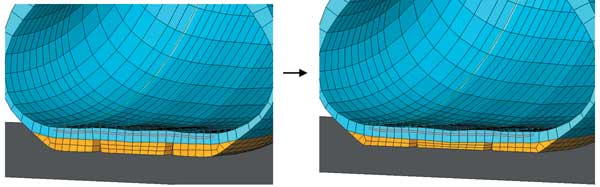
Рис. 19. Сетки для новой и изношенной шин
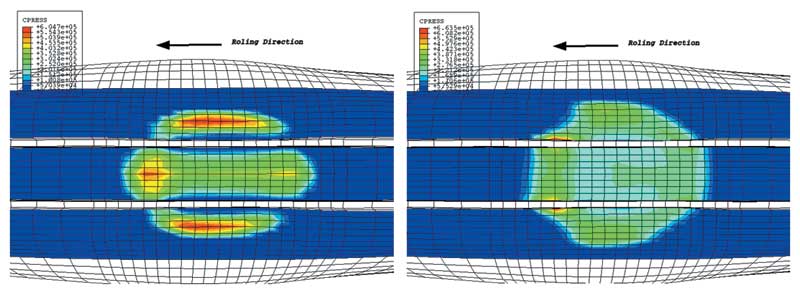
Рис. 20. Распределение контактного давления для новой и изношенной шин
Заключение
С помощью программного комплекса ABAQUS в шинной промышленности можно осуществлять:
• численное моделирование автомобильных шин с учетом нелинейного анализа, включая все виды физических и геометрических нелинейностей:
• расчет поведения шин при статических и динамических нагрузках;
• решение задач наезда шины на бордюр;
• учет широкого спектра моделей материалов, включая все типы резин, в том числе полибутадиеновые каучуки, а также создание собственных моделей материалов;
• учет сложной структуры шины (корд плюс резина) и их совместной работы;
• оптимизацию структуры шины, например рисунка протектора, характеристик корда;
• моделирование эксплуатации шин при различных условиях с использованием многодисциплинарного анализа (прочность, тепло, гидродинамика, акустика и т.п.);
• импорт/экспорт моделей из всех современных систем геометрического проектирования.
Таким образом, программный комплекс ABAQUS предоставляет специалистам возможность использовать эффективный комплексный подход для проектирования современных шин.
С.А.Рыжов Начальник отдела систем проектирования и инженерного анализа компании «ТЕСИС». К.А.Ильин Старший инженер отдела систем проектирования и инженерного анализа компании «ТЕСИС». А.Н.Варюхин Инженер отдела систем проектирования и инженерного анализа компании «ТЕСИС». |


