Методы применения инструментов Т-FLEX CAD 2D для моделирования разверток поверхностей сложных пространственных форм

Борис Рутенберг

О построении разверток пространственных тел по чертежам в CAD-системах и о преимуществах, получаемых пользователем T-FLEX CAD российской компании «Топ Системы», мы уже писали неоднократно. Речь главным образом шла о простоте и эффективности построения разверток для правильных тел вращения, например прямого усеченного конуса, используемых затем в качестве составляющих частей разверток тел более сложных форм (например, типа тора или «улитки»). При описании методов получения разверток сложных форм обычно отмечалась определенная погрешность, которая является своего рода компенсацией за простоту решения.

Однако на практике нередко встречаются задачи, выходящие за границы, которые очерчены возможностью приведения составляющих элементов к правильным формам или допустимостью определенных погрешностей. Решение подобных задач в T-FLEX CAD 2D возможно, но с помощью одних лишь приемов начертательной геометрии и готовых типовых элементов выполнение их оказывается достаточно трудоемким, хотя в T-FLEX CAD 2D и имеется исчерпывающий набор инструментов. Связано это с необходимостью проведения большого числа дополнительных построений. Очевидно, что без глубокой методической проработки и детерминации типовых элементов форм осложняется использование более эффективных инструментов T-FLEX CAD, которые позволяют свести такие задачи к типовым решениям. В данной статье мы намерены предложить читателям свой опыт применения полного арсенала T-FLEX CAD 2D для подобных задач. Благодаря возможностям применения как начертательной, так и аналитической геометрии, описываемый ниже метод, на наш взгляд, вполне отвечает требованиям достижения необходимой степени точности и в то же время обеспечивает вполне приемлемую трудоемкость моделирования достаточно сложных задач. В практике проектирования агрегатных станков и автоматических линий такие задачи встречаются довольно часто, например при проектировании желобов для сбора и отвода отработанной смазочно-охлаждающей жидкости, различных воздуховодов систем вентиляции и т.п. К типовым элементам таких конструкций могут быть отнесены участки перехода между двумя произвольно расположенными в пространстве окружностями, а также из окруж­ности в произвольно наклоненный к ней многоугольник.

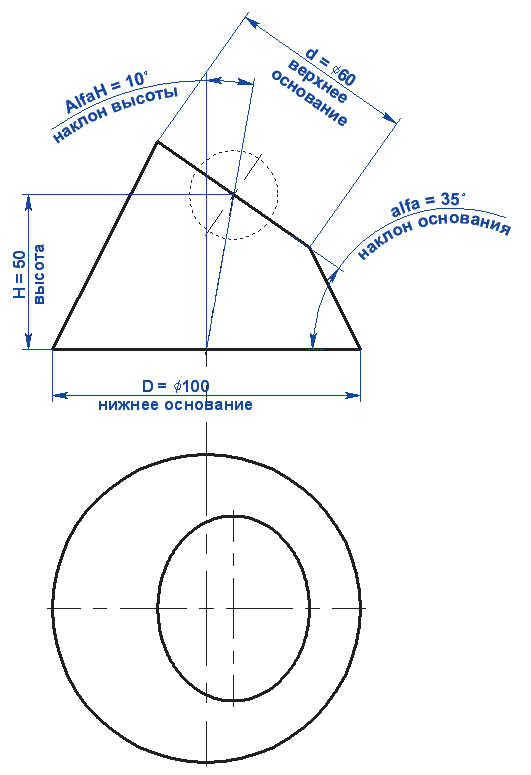
Рис. 1

На рис. 1 изображен чертеж элемента, образованного двумя окружностями диаметрами D и d, наклоненными друг к другу в пространстве углами a (угол наклона линии их центров к нижнему основанию) и j (угол наклона верх­него основания к линии центров).

В T-FLEX CAD имеются мощные средства для параметрического описания такой модели, которые без программирования позволяют модифицировать ее, изменяя названные параметры D, d, и , и трансформировать во всевозможные элементарные формы, примеры которых приведены на рис. 2.

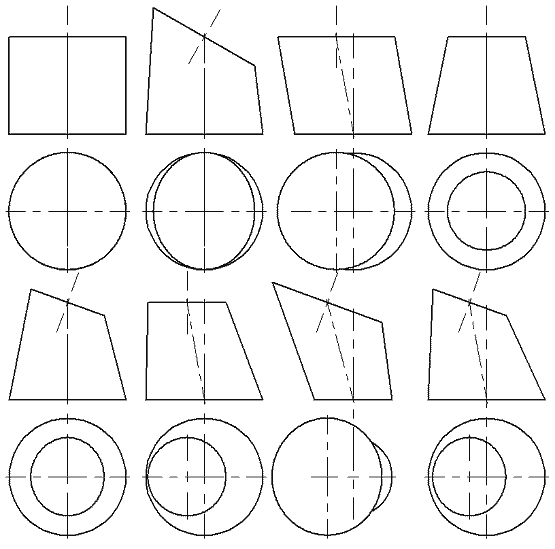
Рис. 2

Из разверток этих элементарных поверхностей могут составляться развертки большого класса различных сложных поверхностей всевозможных конфигураций, например торов, «улиток» и т.п. (рис. 3). Обеспечение необходимой точности достигается увеличением количества элементов, на которые разбиваются сложные поверхности.

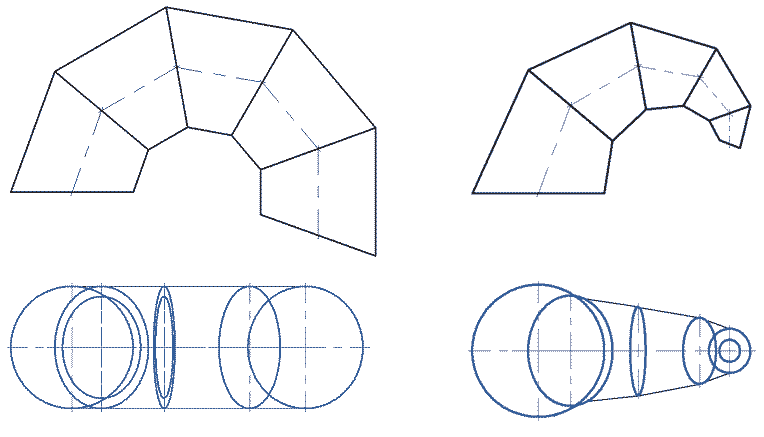
Рис. 3

Для построения типовой модели развертки такого элемента в T-FLEX CAD 2D используются инструменты построения, с помощью которых методами начертательной геометрии производятся дополнительные построения (рис. 4).

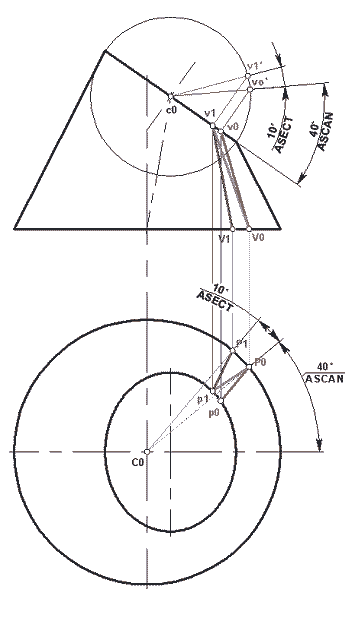
Рис. 4

На виде спереди дополнительно строится проекция верхнего основания и проводятся из центра с0 два луча, один из которых откладывается под углом, задаваемым переменной ASCAN к линии, определяющей плоскость верх­него основания, а второй — под углом к первому лучу, задаваемым переменной ASECT . Таким же образом на виде в плане проводятся два луча из центра С0 , первый из которых откладывается под углом к оси абсцисс, задаваемым переменной ASCAN , а второй — под углом к первому лучу, задаваемым переменной ASECT .

Точки пересечения всех лучей с соответствующими окружностями оснований откладываются на проекции верхнего и нижнего оснований на видах спереди и в плане, давая соответственно точки v0, v1, p0 и p1 на проекциях верхнего основания и V0, V1, P0 и P1 на проекциях нижнего основания. Соединяя полученные таким образом точки, строим проекции образующих p0-P0, p1-P1 и v0-V0 , v1-V1 , а также диагоналей p1-P0 и v1-V0 некоторого сектора конической поверх­ности.

С помощью имеющихся средств T-FLEX CAD в специальном редакторе переменных замеряются длины полученных проекций, по которым вычисляются длины построенных образующих и диагоналей сектора.

,

где: L — длина отрезка (образующей или диа­гонали);

Lv — длина проекции отрезка на вид спереди;

Yp1 и Yp2 — расстояние между координатами Y концов этого отрезка на виде в плане.

Длины дуг верхнего и нижнего оснований LD и Ld вычисляются с помощью выражения:

L =3,14xDxASECT/360,

где: L — длина дуги;

D — диаметр окружности основания;

ASECT — угол сектора.

Далее используются имеющиеся в T-FLEX CAD инструментальные средства (рис. 5), которые позволяют произвести анимацию модели, с заданными параметрами, с сохранением результатов вычислений длин отрезков при каждом шаге в базе данных. Изменяемым параметром при анимации является угол ASCAN , который меняется в пределах от 0 до 180° — с учетом симметричности элемента. Число шагов и соответственно количество секторов развертки задается углом сектора ASECT , чем обеспечивается требуемая точность построения будущей развертки. В приведенном примере задается величина ASECT  = 5°.

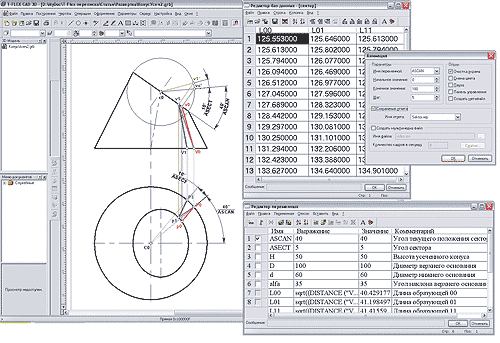
Рис. 5

Дополнительно в T-FLEX CAD создаются модели сектора (рис. 6) и модель развертки (рис. 7) — как сборочная единица, включающая эти секторы в качестве внешних фрагментов. Размеры сторон и диагонали сектора специальными средствами T-FLEX CAD связываются с записями полученной в результате анимации базы данных. Затем этот сектор наносится на сборочную модель развертки в количестве равном числу шагов анимации, причем в каждом вставляемом таким образом фрагменте задается очередной номер, соответствующий строке в базе данных, из которой считываются его параметры. Из точек фрагментов образуется искомый контур развертки. Вторая половина развертки получается с помощью зеркального отображения первой.

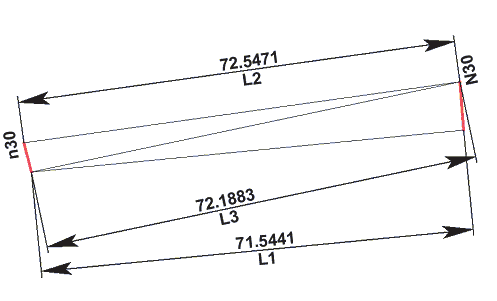
Рис. 6

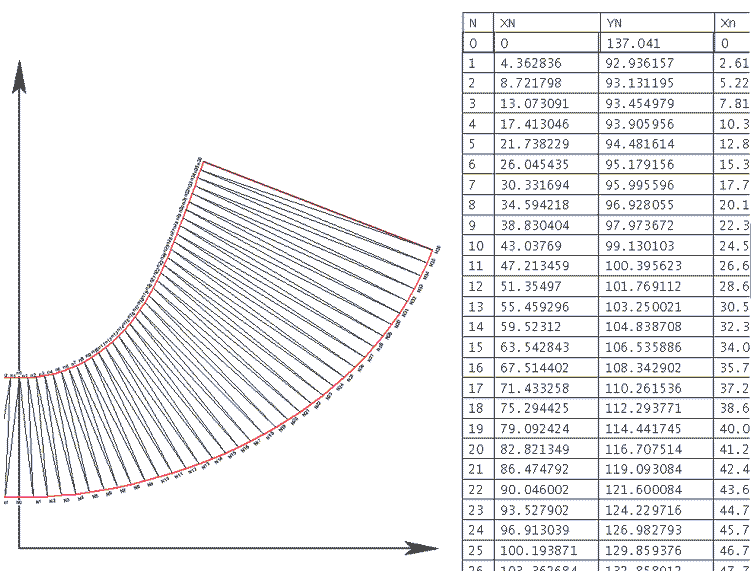
Рис. 7

С помощью еще одного полезного инструмента T-FLEX CAD — автоматической спецификации — создается таблица координат точек контура, считываемых из нанесенных на развертку фрагментов секторов, которая может быть использована для разметки на координатных машинах.

Уменьшая размер сектора, мы можем до­стичь повышения точности — при этом трудоемкость несколько увеличивается за счет увеличения числа фрагментов. Остается добавить, что трансформация полученных таким образом моделей для получения разверток любого типа или при изменении размеров элемента достигается только путем изменения параметров исходного элемента.

Подобным образом можно решать и по­строение разверток других типовых элементов.

Приведем еще один пример построения развертки распространенного элемента поверхности перехода из круга в прямоугольник, который может быть аналогично использован в случае, если вместо прямоугольника применен любой многоугольник.

На рис. 8 изображен чертеж такого элемента, образованного прямоугольным основанием длиной H и шириной B и круглым основанием диаметром D , причем они наклонены друг к другу в пространстве.

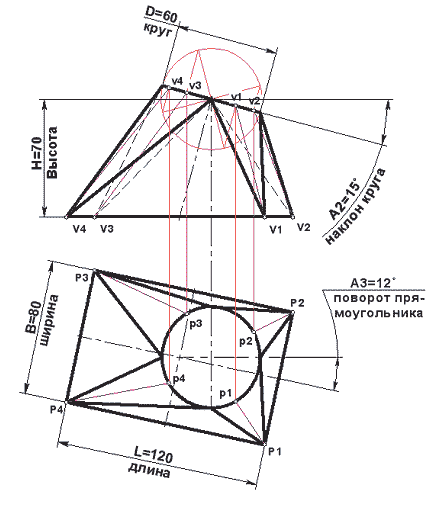
Рис. 8

Для построения типовой модели развертки этого элемента в T-FLEX CAD 2D также производятся дополнительные построения (рис. 9). На виде спереди строится проекция верхнего основания, и из центра с0 проводятся два луча, один из которых откладывается под углом, задаваемым переменной ASCAN к линии, определяющей плоскость верхнего основания, а второй — перпендикулярно первому лучу.

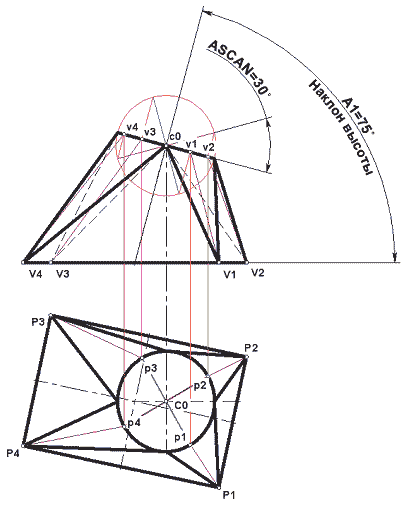
Рис. 9

Точки пересечения лучей с окружностью верхнего основания проектируются на проекцию верхнего оснований на виде спереди, давая, таким образом, соответственно точки v1, v2, v3 и v4, а на виде в плане — точки V1, V 2, V 3 и V 4 . Соединяя полученные таким образом точки с соответствующими вершинами прямоугольников на проекциях нижнего основания, получаем проекции образующих конических участков перехода из прямоугольника в окружность.

С помощью редактора переменных T-FLEX CAD замеряются длины полученных проекций, по которым вычисляются длины построенных таким образом образующих секторов.

,

где: Li — длина образующей i -го участка ( i от 1 до 4);

Lvi — длина проекции этой образующей на виде спереди;

Yp1i и Yp2i — расстояние между координатами Y концов этой образующей на виде в плане.

Затем, аналогично предыдущему примеру, также используется анимация модели с заданным параметрами с сохранением результатов вычислений длин отрезков при каждом шаге в базе данных. Переменным параметром при анимации является угол ASCAN , который меняется в пределах от 0 до 90°. Число шагов определяется углом сектора ASECT , чем обеспечивается требуемая точность построения будущей развертки. В приведенном примере задавалась величина ASECT = 5°.

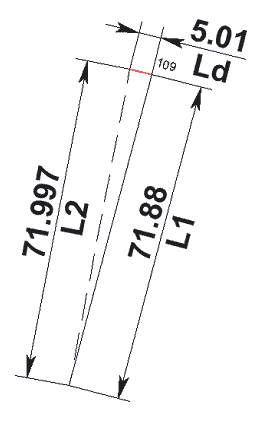
Рис. 10

Дополнительно в T-FLEX CAD создаются модель сектора (рис. 10) и модель разверт­ки (рис. 11) как сборочная единица, включающая эти секторы в качестве внешних фрагментов. Размеры сторон сектора в T-FLEX CAD связываются с записями полученной в результате анимации базы данных. Этот сектор наносится на сборочную модель развертки в количестве равном числу шагов анимации. При этом в каждом вставляемом таким образом фрагменте задается очередной номер, соответствующий строке в базе данных. Из этой базы данных считываются его параметры, а также номер участка, соответствующий номеру колонки в базе данных.

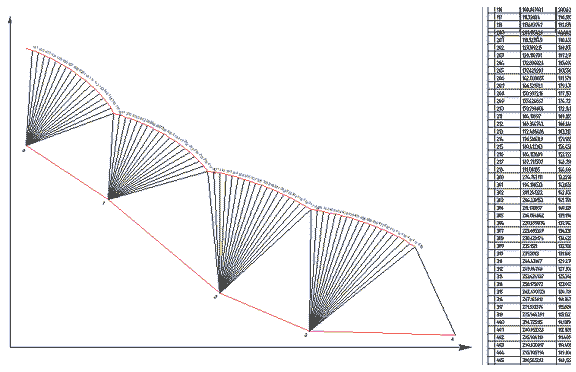
Рис. 11

Длина дуги верхнего основания L вычисляется с помощью выражения:

L = 3,14xdxASECT/360,

где L — длина дуги,

d — диаметр окружности основания;

ASECT — угол сектора.

Названные методы могут быть с большим успехом применены в различных проектах — от вентиляционных систем до ракет и космических станций. Приведенные примеры, возможно, охватывают не весь спектр решаемых задач, однако описанные графоаналитические методы вполне могут быть перенесены на решение других подобных задач. Скажем, если вместо прямо­угольника задача будет содержать какой-либо правильный или неправильный многоугольник, то достаточно будет разработать модели для каждого числа сторон этого многоугольника.

В заключение необходимо отметить, что проектирование и решение сложных математических задач без написания единой строчки программного кода стало доступно любому пользователю, не владеющего азами программирования, благодаря уникальным возможностям и инструментальному обеспечению T-FLEX CAD.

«САПР и графика» 8'2004