Возможности FlowVision в построении моделей для исследования процессов удаления отложений в нефтяных резервуарах
Анализ вариантов постановки задачи в программном комплексе FlowVision
Упрощение расчетной модели формирования струи от винта
Для хранения нефти и нефтепродуктов, для их рационального использования существуют вместительные емкости, так называемые вертикальные цилиндрические стальные резервуары (РВС). Вследствие их огромных размеров (вместимость до 100 тыс. м3) и повышенной экологической опасности к обеспечению надежности их функционирования предъявляются повышенные требования. Существующий подход к проектированию и обследованию технического состояния этих сложных конструкций предусматривает использование при расчетах большого количества коэффициентов, обеспечивающих определенный запас прочности. Введение в эксплуатацию различных устройств и нового оборудования, например перемешивающего устройства либо устанавливаемых на крышке овального или круглого люков-лазов, вносящих дополнительную нагрузку на стенку РВС, влечет за собой необходимость исследования напряженно-деформированного состояния (НДС) резервуара с учетом работы последних. Для проведения упомянутых расчетов требуется знать характеристики возникающего движения жидкости внутри резервуара, вследствие чего можно сделать попытку использования в этих целях программного комплекса FlowVision.
Областью, где исследуется течение, является резервуар со следующими габаритными размерами: высота — 12 м, диаметр — 45,6 м. Резервуар, заполнен нефтью, содержащей слой уплотненного парафинистого осадка. В качестве перемешивающего устройства служит винт диаметром 0,7 м, который расположен вблизи дна резервуара, частично в слое осадка. При вращении винт создает сканирующую по дну резервуара струю. Период сканирования — 2ч, угол сканирования — 60°. Заполнение резервуара нефтью варьировалось в диапазоне от 4 до 12 м. Высота уплотненного осадка принята равной 1 м.
Практический интерес при решении поставленной задачи представляет получение картины течения в резервуаре (поле скоростей), изменения во времени распределения по объему концентрации парафинистого осадка, а также картину распределения динамического давления от струи винта на стенки резервуара.
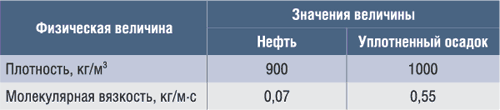
Известно, что физические свойства нефти (плотность, вязкость и т.д.) значительно отличаются в зависимости от места ее добычи. В табл. 1 приведены диапазоны изменения указанных величин.
Физические свойства уплотненного осадка также могут весьма заметно различаться — разные источники дают значительный разброс данных.
С учетом вышесказанного при отработке расчетной модели были приняты физические характеристики нефти и ее уплотненного осадка, приведенные в табл. 2.
Таблица 1. Свойства нефти

Таблица 2. Расчетные характеристики
Анализ вариантов постановки задачи в программном комплексе FlowVision
В настоящее время программный комплекс FlowVision позволяет провести постановку задачи в полном объеме, то есть в качестве исходной будет служить модель движения двухфазной несжимаемой жидкости (рис. 1): внутренняя полость резервуара полностью или частично заполняется нефтью, через «фильтр» около дна резервуара подается слой уплотненного осадка (рис. 2). Затем там же размещается (например, посредством модуля подвижного тела) винт, вращается с заданной требуемой частотой (рис. 3). В результате получается картина течения жидкости в резервуаре и, как следствие, перемешивания нефти с уплотненным осадком. На начальном этапе авторы пошли именно по пути полной постановки задачи. Исключением было только то, что вращение винта задавалось не как программное движение подвижного тела, а с использованием специального модуля программы — модуля для вращающихся тел. Особенность использования этого модуля заключается в построении выделенной области; в данном случае — вокруг винта с вращающейся вместе с ним расчетной сеткой. Не вдаваясь в подробности, отметим, что использование указанного модуля позволяет в данной постановке задачи значительно повысить точность расчета.
Построенная таким способом расчетная модель, адекватно описывающая и течение в резервуаре, и формирование струи от винта, как показали результаты, требует для проведения расчетов значительных вычислительных ресурсов — большой оперативной памяти компьютера (не менее 1 Гбайт) в сочетании со значительным количеством итераций на проведение самого расчета.
Полученный результат объясняется наличием в задаче двух физических процессов, различных по пространственным масштабам и по времени:
1. Мелкомасштабный и быстротекущий процесс — вращение винта и формирование струи жидкости за ним. Этот процесс происходит в области, ограниченной лопастями винта, которые имеют характерный размер — не более нескольких дециметров. Таким образом, для правильного описания течения в зоне расположения винта характерный размер расчетных ячеек должен измеряться долями сантиметра. для адекватного формирования струи за вращающимся винтом характерный шаг по времени, согласно требованиям расчетного метода, определяется сотыми долями периода вращения винта и для рассматриваемых частот вращения (порядка 600 об./мин) равен тысячным долям секунды.
2 Крупномасштабный и медленно развивающийся процесс — формирование течения в самом резервуаре. Этот процесс имеет пространственный масштаб, определяемый габаритными размерами емкости (диаметр резервуара), то есть порядка десятков метров. Скорости течения при этом измеряются от единиц метров в секунду вблизи устройства смешения до долей метра в секунду на периферии от него. Как следствие, характерные размеры расчетных ячеек составляют несколько дециметров, а время процесса, то есть время перемешивания слоя парафинистого осадка с нефтью, — от нескольких минут и зависит от плотности слоя осадков.
Следовательно, в полнообъемной постановке задачи присутствуют как крупные ячейки для описания развития течения в резервуаре в целом, так и мелкие — в зоне, где расположен винт. Такая резко разномасштабная расчетная модель, как правило, имеет высокую размерность (общее количество расчетных ячеек), что предъявляет повышенные требования к объему оперативной памяти компьютера.
Как говорилось выше, время полного счета задачи определяется временем перемешивания, а шаг по времени — разрешением течения около винта. В результате получаем, что для расчета задачи в полной постановке требуется несколько десятков, а может, и сотен тысяч временных итераций, что с учетом повышенной размерности модели по количеству расчетных ячеек может потребовать нескольких недель непрерывного счета одного варианта. Естественно, такая ситуация не может удовлетворить расчетчика, проводящего, например, серийные расчеты нагрузок (давления) на стенки резервуара для обоснования выбора конструкции емкости, или расчеты характеристик самого течения для обоснования эффективности того или иного устройства перемешивания. Для обеспечения эффективного использования программы при решении указанных проблем необходимо упрощение постановки задачи.
На основе проведенного анализа полнообъемной постановки задачи определяются и пути упрощения задачи. В частности, разумной кажется замена процедуры формирования струи за винтом готовым решением, которое описывает основные характеристики течения (суммарный расход струи, распределение скоростей, динамическое давление).
Для поиска такого решения отдельно была поставлена задача по расчету течения в струе за винтом. Решение было получено для безграничной жидкости в рамках модели несжимаемой жидкости с использованием модуля вращающихся тел. В качестве перемешивающего устройства рассмотрен трехлопастной винт диаметром 0,7 м, вращающийся с частотой 600 об./мин. Геометрия винта представлена на рис. 4. В качестве рабочей жидкости взята нефть с плотностью и молекулярной вязкостью, приведенными в табл. 2.
На рис. 5 показаны картина поля скоростей и график осевой составляющей скорости. Как видно из рисунка, непосредственно за винтом радиальная составляющая скорости жидкости заметно изменяется, при этом скорость потока меняет величину и направление. Осевая составляющая скорости имеет ярко выраженный максимум, который расположен примерно на 0,65-0,70 радиуса винта. Изменение направления вектора скорости в диаметральной плоскости приводит к сужению струи на начальном участке. При этом углы отклонения вектора скорости от оси, как показали расчеты, могут достигать 30°.
На рис. 6 приведены картина поля скоростей и график тангенциальной составляющей скорости. Видно, что непосредственно за винтом струя имеет значительную крутку. Тангенциальная составляющая скорости возрастает с ростом расстояния от оси вращения, достигая своего максимума на 0,80-0,85 радиуса винта.
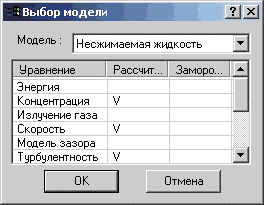
Рис. 1. Выбор модели
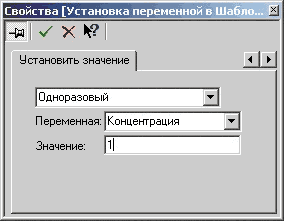
Рис. 2. Задание слоя осадков
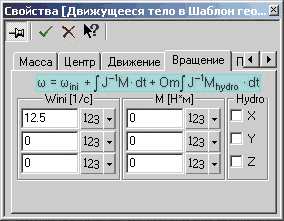
Рис. 3. Задание вращения винта

Рис. 4. Винт
Все отмеченные выше особенности течения жидкости в непосредственной близости от винта связаны с принципом действия данного перемешивающего устройства. Естественно, что с удалением от винта струя жидкости должна терять эти особенности и приближаться по своим характеристикам к характеристикам классической затопленной струи.
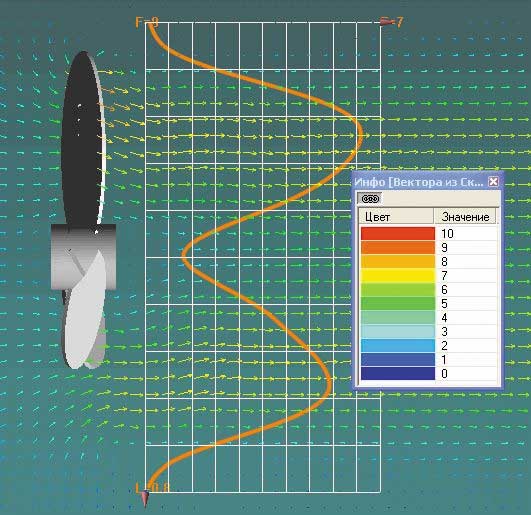
Рис. 5. Поле скоростей в плоскости, перпендикулярной плоскости винта
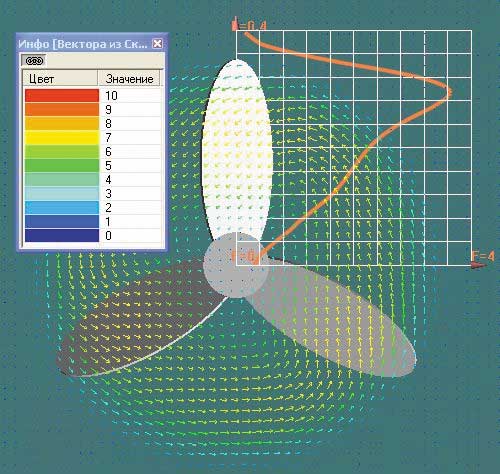
Рис. 6. Поле скоростей в плоскостивинта
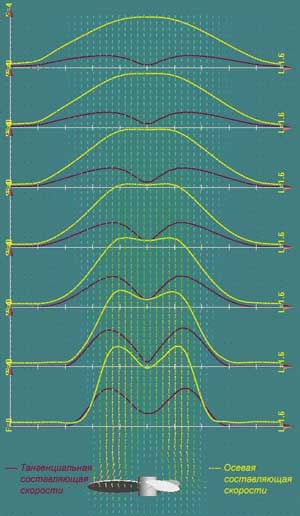
Рис. 7. Графики осевой и тангенциальной составляющих скорости
На рис. 7 приведены поле скоростей и графики изменения осевой и тангенциальной составляющих скорости струи по мере удаления от винта. Пространственный шаг, с которым построены графики, составляет половину диаметра винта — 0,35 м. Диапазон расстояний — до трех с половиной диаметров винта, то есть 2,45 м. Как видно из рисунка, уже на расстояниях свыше двух с половиной диаметров от плоскости винта, что в нашем случае соответствует примерно 1,8 м, струя имеет один максимум, расположенный на оси винта. Тангенциальная составляющая скорости, характеризующая закрутку струи, также быстро уменьшается по мере удаления от плоскости винта. Поджатие струи, как видно из направления векторов поля скоростей, прекращается еще раньше. Таким образом, на расстоянии 2,5 м и более от плоскости винта структура течения в струе уже практически не имеет особенностей, связанных с данным типом перемешивающего устройства. С учетом характерных размеров резервуара (диаметр — 45,6 м), получаем, что струя теряет индивидуальные особенности на расстоянии менее 5% характерной длины пути в резервуаре. Таким образом, на основной части траектории струи ее характеристиками будут импульс и расход, в сочетании со структурой течения, близкой к структуре затопленной струи.
Упрощение расчетной модели формирования струи от винта
Перейдем к описанию построения схематизации описанного перемешивающего устройства диском, наделенным интегральными характеристиками (расход жидкости) устройства перемешивания. В качестве упрощенной модели винта рассмотрим диск (рис. 8) того же диаметра и с тем же расходом жидкости, что и винт. Характеристики производительности перемешивающего устройства можно взять либо из документации, либо, как поступили авторы, из расчета течения за винтом.
Одну плоскость винта назовем «выход диска» и зададим на ней скорость втекания в расчетную область жидкости (рис. 9), другую — «вход диска», задав на ней скорость вытекания, численно равную скорости втекания, но с обратным знаком. На боковой грани диска зададим условие стенки с проскальзыванием.
Приведенный вариант упрощения можно назвать своеобразным «приближением нулевого уровня». Во-первых, на выходной плоскости диска задано равномерное распределение скорости, что явно не соответствует распределению скорости как за винтом, так и в затопленной струе. Далее: в рассматриваемом варианте нет ни крутки струи, ни направления векторов скорости во внутреннюю часть струи. Рассмотрим структуру потока за диском. Поле скоростей и распределение осевой скорости в зависимости от расстояния до диска приведено на рис. 10. Пространственный шаг, с которым построены графики, такой же, как и в случае с винтом, — половина диаметра диска, то есть 0,35 м. Диапазон расстояний — до трех с половиной диаметров диска, то есть 4,55 м. Как видно из приведенных материалов (см. рис. 10), с удалением от диска эпюра скоростей трансформируется, постепенно переходя к распределению скоростей все той же классической затопленной струи. И на том же расстоянии от диска (три с половиной диаметра) эпюра распределения осевой скорости по форме приближается к эпюре, полученной в случае расчета течения за винтом.

Рис. 8. Диск
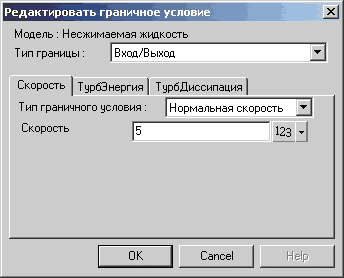
Рис. 9. Граничные условия на выходе диска
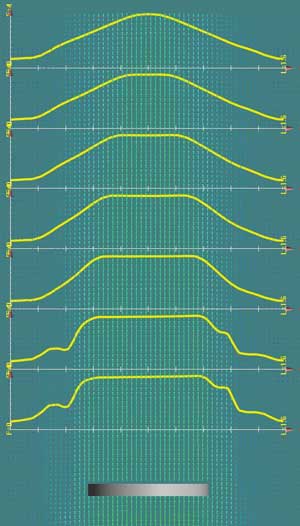
Рис. 10. Графики осевой составляющей скорости на различных расстояниях за диском
Более тщательное сравнение эпюр осевых скоростей для рассмотренных случаев приведено на рис. 11, где показаны поделенные на максимальные значения эпюры скоростей для сечения, отстоящего от плоскостей диска/винта на три с половиной диаметра (2,45 м). Видно, что даже такая грубая замена реального перемешивающего устройства позволяет, начиная с определенного расстояния, получить практически совпадающий по форме распределения осевой скорости поток жидкости. При этом расход жидкости, проходящий через диск, был задан в граничных условиях равным расходу через устройство перемешивания.
В заключение остановимся на дополнительных возможностях программного комплекса FlowVision по моделированию струй.
В принципе, программный комплекс FlowVision позволяет на выходе диска смоделировать все характеристики струи — крутку, поджатие, распределение скорости по плоскости диска, а также характеристики турбулентности потока.
Для реализации заданной закрутки струи, ее поджатия и эпюры распределения скоростей в граничном условии «Вход/выход» на вкладке «Скорость» имеется тип граничного условия под названием «Закрутка скорости», с помощью которого можно задать:
• «частоту вращения», которая через соотношение V=RxW будет определять тангенциальную составляющую скорости жидкости, а также направляющие орты вектора угловой скорости: Ax, Ay, Az (рис. 12);
• скорость истечения жидкости (рис. 12);
• угол разлета, отрицательное значение которого определяет поджатие струи (рис. 13).
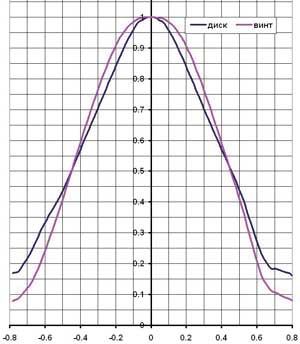
Рис. 11. Нормированные эпюры скоростей за винтом и диском
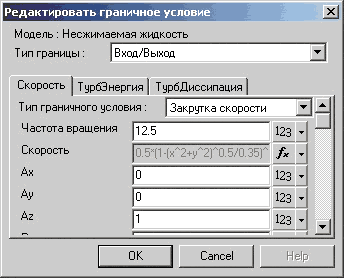
Рис.12. Задание крутки струи
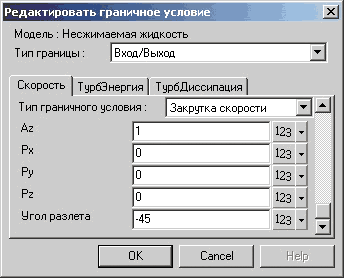
Рис.13. Задание поджатия струи
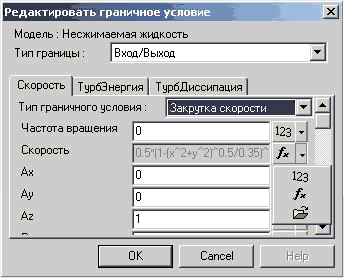
Рис. 14. Варианты представления величин
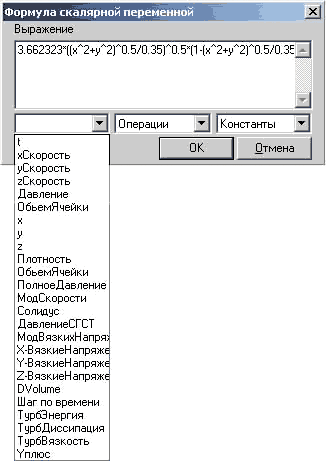
Рис. 15. Задание переменной по формуле
При этом, указанные величины могут быть заданы как постоянными значениями, например частота вращения и угол разлета, так и в виде функции (скорость истечения). Тот или иной вид представления определяется пользователем в соответствующем всплывающем меню (рис. 14). Символ «123» — задание постоянным числом, символ «fx» — функциональное представление. Для функционального задания той или иной физической величины после выбора данного представления пользователь, нажав на символ «fx», открывает соответствующее диалоговое окно, где и задает формулу, определяющую значения величины (рис. 15). При этом, как видно из рисунка, пользователю для задания формулы доступны все переменные, присутствующие в расчете (выпадающий список «Переменные»), включая пространственные координаты, а также необходимый набор элементарных функций (выпадающий список «Операции»). На представленном рисунке виден пример реализации эпюры скорости на выходе из диска по следующей формуле:
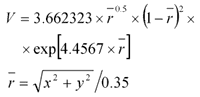
На рис. 16 показаны поле скоростей и распределение осевой скорости в зависимости от удаления диска, в котором задана приведенная в примере эпюра распределения скоростей, учтена крутка, а также поджатие струи. Как видно, в данном случае, который, в отличие от предыдущего можно назвать «приближением более высокого порядка», структура потока больше похожа на структуру потока за винтом.
Таким образом, программный комплекс FlowVision имеет развитой механизм моделирования потоков за различными устройствами, что позволяет эффективно упрощать постановку и решение сложных технических задач.
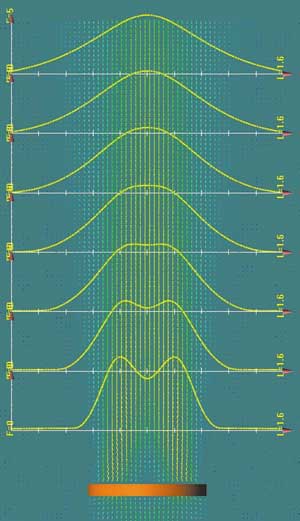
Рис. 16. Графики осевой составляющей скорости на различных расстояниях за диском
Построение расчетной модели по исследованию течения в резервуаре в процессе перемешивания нефти с осадками
В качестве исходной модели была выбрана модель двухфазной (нефть и уплотненный осадок) несжимаемой жидкости (рис. 17). В рамках данной модели решаются уравнения: Навье-Стокса (скорость), турбулентной энергии и ее диссипации (турбулентность), а также определяется распределение концентрации веществ: нефти и уплотненного осадка (концентрация). При этом в качестве модели массопереноса была выбрана модель массовой концентрации (рис.18), которая описывает процесс перемешивания растворимых веществ, что соответствует рассматриваемым компонентам.
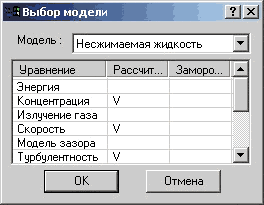
Рис. 17. Выбор исходной модели
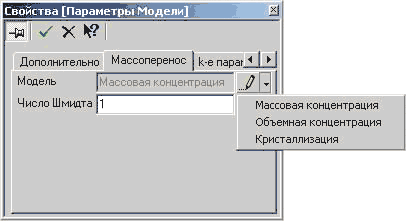
Рис. 18. Выбор модели массопереноса
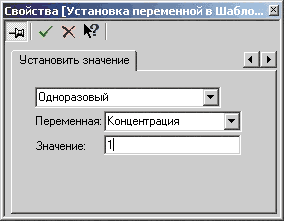
Рис. 19. Задание слоя осадков
Задание слоя уплотненного осадка проводилось с использованием фильтра «Установка переменной» одноразового включения в начальный момент расчета (рис. 19). Во всех расчетных случаях высота слоя осадка принималась равной 1 м.
С учетом результатов исследований, проведенных с целью упрощения полнообъемной расчетной модели, винт был заменен диском, который вводился при помощи фильтра «Движущееся тело». Данный способ импорта в расчетную область различных объектов удобен, в частности, тем, что позволяет задавать пространственное положение объекта (рис. 20), а также, например, его линейное и угловое перемещения в пространстве расчетной области.
В выполненных расчетах центр диска был расположен в 1 м от дна резервуара и в 20 м от его центра. Его плоскость была повернута на 30° относительно стенки резервуара и наклонена на 5° к его дну.
Физические свойства нефти и уплотненного осадка во всех расчетах соответствовали приведенным в табл. 2.
Необходимо отметить, что для высот заполнения резервуара нефтью, превышающих 4 м, расчетная область ограничивалась по высоте этой величиной. Анализ выполненных вычислений показал, что все наиболее характерные процессы при перемешивании нефти и уплотненного осадка происходят в слое, толщина которого не превышает указанную величину.
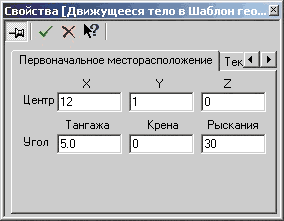
Рис. 20. Задание положения диска
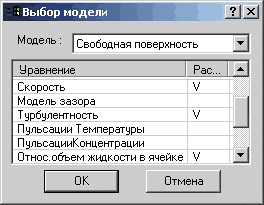
Рис. 21. Модель для небольших высот заполнения резервуара нефтью
Моделирование течения через такую границу резервуара проводилось с использованием граничного условия «Свободный выход» с нулевым давлением, а давление со стороны не включенного в расчет объема нефти входило в опорное значение как добавка к атмосферному давлению. Удаление «малоэффективной» части резервуара способствовало также уменьшению количества расчетных ячеек модели.
Для исследования течения при небольших высотах заполнения резервуара нефтью, не превышающих 4 м, использовалась модель свободной поверхности (рис. 21), которая в качестве базовой имеет ту же модель несжимаемой жидкости, но дополняется уравнениями определения границы раздела сред, в нашем случае — «воздух—нефть» («Относительный объем жидкости в ячейке»).
Расчетная сетка моделей во всем объеме резервуара, за исключением объема вокруг перемешивающего устройства и вблизи верхней границы резервуара, содержала ячейки нулевого уровня размером 0,5x0,5 м в горизонтальной плоскости и 0,25 м по вертикали. На стенках и в полуметровом слое на границе раздела «нефть—уплотненный осадок», а также в полуметровом слое по границе раздела «нефть— воздух» для модели со свободной поверхностью была применена адаптация расчетных ячеек 1-го уровня.
В области расположения перемешивающего устройства (диска) ячейки нулевого уровня были размером 0,25x0,25x0,25 м по всем направлениям (рис. 22). Дополнительно на поверхности диска была применена адаптация 2-го уровня, то есть входная и выходная поверхности диска диаметром 0,7 м были разбиты не менее чем на 70 ячеек.
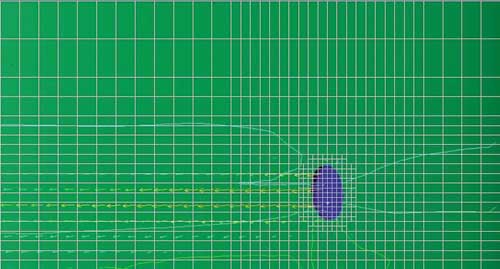
Рис. 22. Расчетная сетка
Результаты расчета
Расчеты, выполненные на построенной модели, позволили получить картину течения в резервуаре при работе перемешивающего устройства. Итоговыми результатами расчета для анализа течения в процессе перемешивания были:
• поле скоростей;
• распределение концентрации осадка;
• распределение давления по боковым стенкам и дну резервуара.
На рис. 23 представлены отдельные фазы развития процесса перемешивания в резервуаре в течение первых 20 с после начала работы устройства перемешивания. Здесь хорошо видны формирование фронта «волны», которая обусловлена появлением вихревого течения в момент включения устройства, а также динамика процесса перемешивания нефти с осадком после этого фронта.
На рис. 24 приведено поле скоростей в непосредственной близости от дна резервуара и распределение избыточного давления на самом дне. Видно «скоростное пятно» от струи на дне резервуара и формирование обратного течения в придонном слое, которое обусловлено избыточным давлением струи на дно и боковую стенку резервуара.
Таким образом, проведенные расчеты показали возможность получения с помощью программного пакета FlowVision необходимой информации о картине течения в виде полей скорости, о процессе перемешивания в виде распределения концентрации осадка и дополнительных нагрузок, действующих на конструкции резервуара, в виде распределения давления.
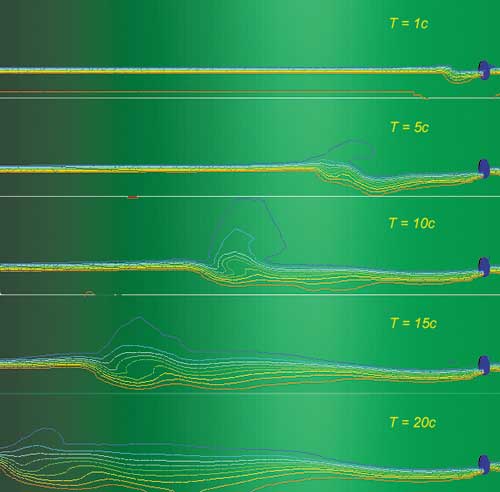
Рис. 23. Фазы развития процесса перемешивания в резервуаре

Рис. 24. Поле скоростей и распределение избыточного давления на дне резервуара
Заключение
В результате проведенной работы:
• осуществлен анализ физических аспектов постановки задачи о течении в резервуаре в процессе перемешивания нефти с уплотненным осадком применительно к моделированию в программном комплексе FlowVision;
• выполнен анализ различных вариантов расчетных моделей для решения задачи при моделировании в программном комплексе FlowVision;
• найдены пути упрощения полнообъемной расчетной модели:
- выделение в отдельную задачу определения характеристик потока за устройством перемешивания,
- использование возможностей программного пакета FlowVision по моделированию требуемых условий истечения, что позволило ввести в расчетную модель готовое решение по формированию течения за устройством перемешивания и тем самым значительно сократить время расчетов;
• сделано обоснование проведенного упрощения расчетной модели;
• в полученной модели проведены систематические расчеты, которые показали возможность получения с помощью программного пакета FlowVision необходимой информации о картине течения в виде полей скорости, о процессе перемешивания в виде распределения концентрации осадка и дополнительных нагрузок, действующих на конструкции резервуара, в виде распределения давления.
И.Э.Лукьянова Канд. техн. наук, доцент, УГНТУ (г.Уфа). В.В.Шмелев Руководитель центра технической поддержки программных продуктов, ООО «ТЕСИС» (г. Нижний Новгород). |


