Моделирование рабочих процессов аксиально-плунжерных гидромашин как часть методики виртуальной разработки и сопровождения изделий
Аксиально-плунжерные гидромашины (АПГМ), работающие на самовсасывание рабочей жидкости, предназначены для применения в приводах с открытыми схемами. К таким приводам обычно относятся гидросистемы гражданских мобильных машин и приводы станочного технологического оборудования. Условия эксплуатации гидромашин достаточно жесткие, и требования к надежности и ресурсу непрерывно повышаются. Разработчики и производители аксиально-поршневых гидромашин постоянно испытывают давление рынка. Им одновременно приходится решать две задачи: с одной стороны, как можно быстрее разрабатывать и ставить на производство новые образцы гидромашин, а с другой — постоянно повышать их качество и надежность. Решить поставленные задачи возможно только с применением последних достижений науки и новейших информационных технологий. Одно из последних и наиболее эффективных направлений автоматизации конструкторско-технологических работ — создание методики виртуальной разработки и сопровождения машиностроительных изделий. Частью этой методики являются методы исследования рабочих процессов гидромашин, основанные на математическом моделировании.
Проектирование АПГМ в основном базируется на общих машиностроительных методиках расчета деталей и механизмов и на огромном систематизированном опыте практической эксплуатации этих объектов. В традиционной методике проектирования значительное место (до 30-50% общих затрат), по мнению И.И.Бажина, составляют затраты на экспериментально-доводочные исследования и испытания, а также на доработку по выявленным в результате испытаний дефектам. Поэтому задача автоматизации процесса проектирования в рамках методики виртуальной разработки и сопровождения изделия, как и задача углубленных расчетно-теоретических и экспериментальных исследований многообразных и сложных физических явлений и взаимодействий, имеющих место в узлах АПГМ, с использованием современных программ и методов, приобретает особую актуальность, а с учетом достигнутого современного уровня знаний в этой области характеризуется повышенной трудностью.
Один из основных вопросов проектирования аксильно-поршневых машин, работающих в режиме самовсасывания, — определение допустимых частот вращения и максимального значения вязкости рабочей жидкости при отсутствии кавитационного недозаполнения рабочих камер. Кавитационное снижение подачи насоса обусловлено тем, что к концу цикла всасывания поршневые камеры оказываются лишь частично заполненными рабочей жидкостью. Это происходит по причине эффекта парогазовой кавитации или нарушения сплошности среды, рабочей жидкости, находящейся в рабочих камерах насоса, вызванной локальным падением давления всасывания.
Описанию вопросов проектирования АПГМ, работающих в режиме самовсасывания жидкости, посвящено большое количество работ. Предложенные методики основываются на экспериментальном определении соответствующих коэффициентов. Однако течение жидкости в каналах всасывания гидромашины характеризуется сложной пространственной геометрией каналов и полостей, оказывающих существенное влияние на состояние потока жидкости в поршневой камере гидромашины. Решить задачу исследования состояния жидкости в камере насоса можно с использованием специализированного математического аппарата. В качестве такого инструмента мы применяем программу моделирования течения жидкостей и газов Flow-3D (www.flow3d.ru). Модель потока, основанная на модели течения вязкой жидкости в замкнутом пространстве с учетом диссипации энергии и возможности образования кавитационных пустот в потоке, позволяет с достаточной степенью достоверности и с разумными затратами вычислительного времени имитировать процессы всасывания и нагнетания при различных внешних условиях: изменение типа рабочей жидкости, газосодержания, температуры, вязкости, плотности, геометрических и технологических параметров распределителя и крышки АПГМ, частоты вращения вала насоса и т.д.
Динамический процесс всасывания гидромашины в режиме запуска при низких температурах показан на рис. 1. На рисунках отчетливо видны места нарушения сплошности среды и зоны развитой кавитации.



Рис. 1. Состояние жидкости в рабочей камере насоса в цикле всасывания: температура рабочей жидкости — –40 °C; жидкость — масло ВМГЗ; угол отклонения люльки насоса — 6°; частота вращения вала — 1500 об./мин
На работоспособность гидромашин серьезно воздействуют температурные факторы. За исключением внешних воздействий, выделение тепла производится самой гидромашиной за счет трения конструктивных узлов и деталей, а также за счет диссипации энергии рабочей жидкости в результате рабочего процесса. На рис. 2 показаны варианты конструкции, подвергшиеся воздействию факторов повышенной температуры, а также последствия этого воздействия: области материала с фазовыми переходами, следы оплавления, поверхностные трещины.





Рис. 2. Результаты температурного воздействия на детали ходовой части АПГМ
Прежде всего, общее повышение температуры влечет за собой увеличение линейных геометрических размеров деталей ходовой части, провоцируя изменение зазоров.
Вторым по степени температурного воздействия является фактор изменения свойств материала, а также возникновение внутренних напряжений в пограничных контактных слоях биметаллов. Поскольку контактные взаимодействия сопровождаются резким локальным повышением температуры (как видно из приведенных выше рисунков — до критических точек фазовых переходов), а весь механизм омывается рабочей жидкостью, то трибомеханические процессы и температурная картина взаимодействия инвариантны. В обобщенном случае распределение температурных полей по объему конструкции ходовой части АПГМ выглядит так, как показано на рис. 3. А для отдельной детали картина будет такой, как на рис. 4.
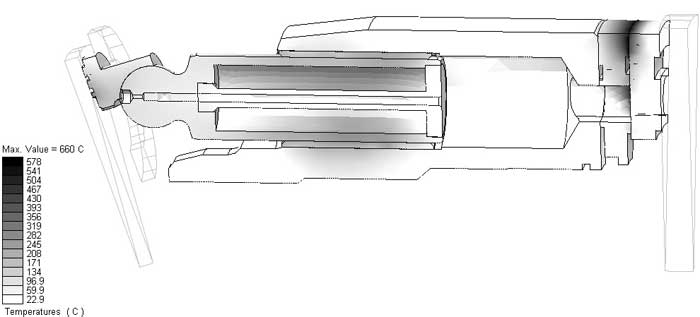
Рис. 3. Распределение температуры
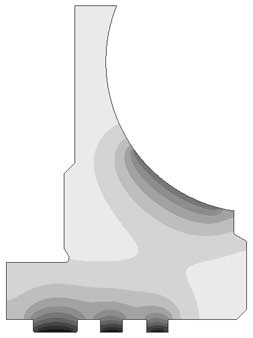
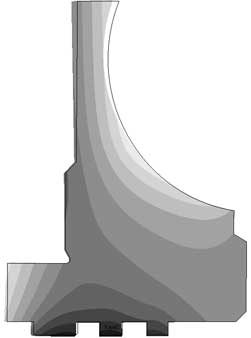
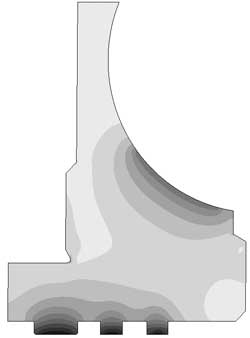
Рис. 4. Распределение: а — температуры; б — температурной деформации; в — температурных напряжений
Величина температуры определяется количеством работы сил трения соприкасающихся деталей. Ее конкретное значение рассчитывается моделированием контактных напряжений и сил. Для моделирования контактных взаимодействий использовался программный комплекс MSC.AFEA (MSC.Patran + MSC.MARC). Эта система обеспечивает комплексный анализ конструкций с учетом сложных трехмерных контактов, больших пластических и упругих деформаций, сложных моделей материалов, значительного изменения температур, циклического нагружения.
По результатам моделирования температурные напряжения составляют 2-5% (в биметаллах — 5-10%) относительно основных (от приложенных силовых нагрузок) напряжений, а температура в зоне контакта изменяется в пределах 50-200 °C. При моделировании учитывались реальные зазоры — конструкторские и технологические допуски и посадки. Их влияние на работоспособность конструктивных элементов нашло отражение и в изменении характеристик контакта сопряженных узлов и общего деформированного состояния деталей.
Несложный расчет по кинематической схеме позволяет установить, что изменение зазора в паре поршень-втулка блока цилиндров на 0,05% (от 0 до 20 мкм) приводит к повышению окружной скорости движения гидростатической опоры относительно опорного диска на 3,9%. Увеличение зазоров в сферической заделке плунжеров влечет за собой увеличение контактных напряжений на сфере. На рис. 5 представлены картины распределения контактных напряжений в конструкции гидростатической опоры (ГСО) при давлении в поршневой камере рн = 45 МПа для различных значений зазоров в сферической заделке: а — д = 0, б — д = 12 мкм, в — д = 25 мкм.
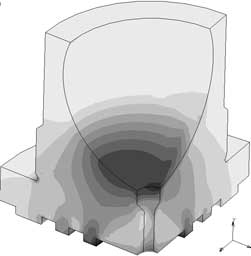
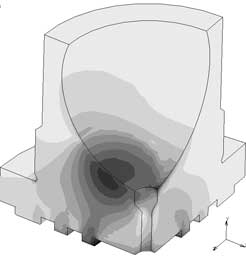
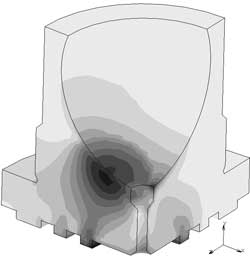
Рис. 5. Контактные напряжения в конструкции ГСО при различных зазорах в сферической заделке
На рис. 6 показана зависимость контактных напряжений в сферической заделке от величины давления в поршневой камере при различных величинах зазоров и шероховатости контактирующих поверхностей.
Используя элементы физической нелинейности (биметаллизация, напыление, поверхностная обработка, композиты и т.д.), проектировщики гидромашин руководствуются стремлением упрочнить конструкцию, снизить эффекты деформации и улучшить показатели контактного взаимодействия. Однако сочетание материалов различной физической природы порождает внутренние напряжения на границе раздела материалов.
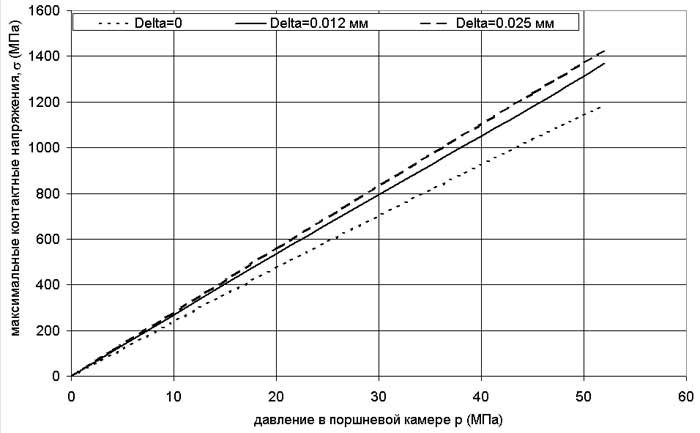
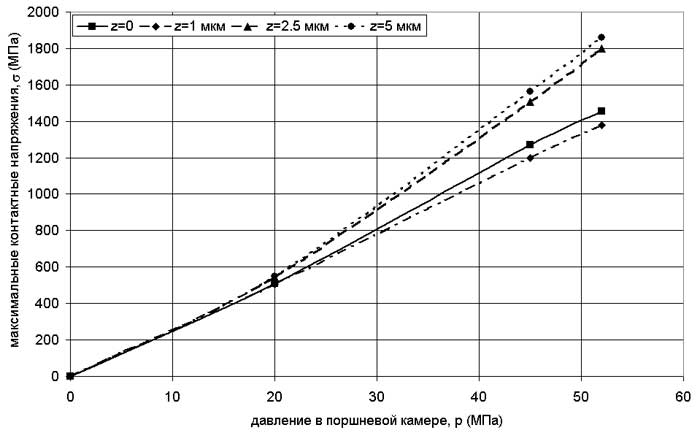
Рис. 6. Изменение контактных напряжений в зависимости от величины зазора и шероховатости контактирующих поверхностей
Так, в случае гидростатической опоры с биметаллизированными контактными поверхностями (рис. 7) контактные напряжения снизились на 13% — в зоне контакта. Однако зона максимальных напряжений сместилась с поверхности контакта вглубь — в область сопряжения «мягкого» контактного слоя с «жесткой» основой. Поэтому при использовании биметаллов определяющее значение приобретает температурная деформация, а в силу различных значений коэффициентов линейного расширения происходит резкое увеличение сдвиговых напряжений.
Изменение формы деталей в результате рабочего процесса АПГМ приводит к изменению формы рабочих зазоров и, как следствие, — к изменению их гидромеханических характеристик. Для определения гидромеханических характеристик жидкостной пленки в рабочем зазоре используем программу Flow-3D, а для определения геометрических параметров зазора — программу MSC.AFEA.
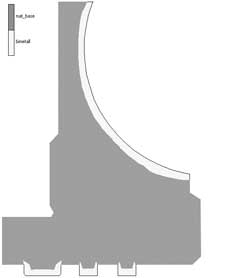
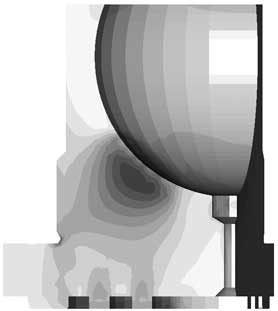
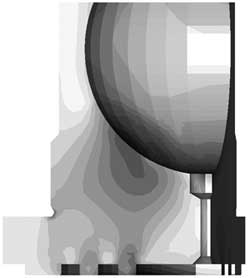
Рис. 7. Модель биметаллизированной ГСО (а); напряжения в биметаллизированной ГСО (б); напряжения в типовой ГСО (в)
Так, в конусном расширяющемся зазоре деформированной ГСО эпюра давления принимает гиперболический характер и площадь этой эпюры меньше площади эпюры плоско-параллельного зазора. Таким образом, у деформированной опоры отжимающее усилие меньше, чем у недеформированной (при том же зазоре). Отметим еще один важный момент. В целом площадь эпюры тем меньше, чем меньше зазор и чем больше перекос втулки. Так, на рис. 8 показаны: 1 — эпюра при зазоре 10 мкм; 2 — эпюра при зазоре 20 мкм.
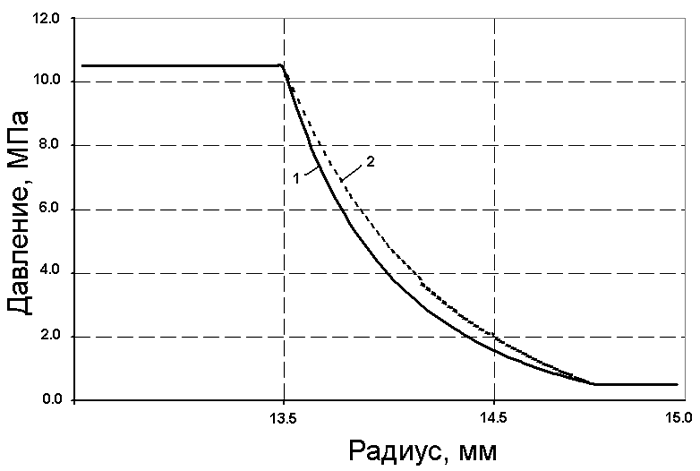
Рис. 8. Эпюры в зазоре ГСО при различных величинах рабочего зазора
Из графика, представленного на рис. 9, видно, что даже незначительная деформация донной части ГСО оказывает существенное воздействие на форму рабочей эпюры.
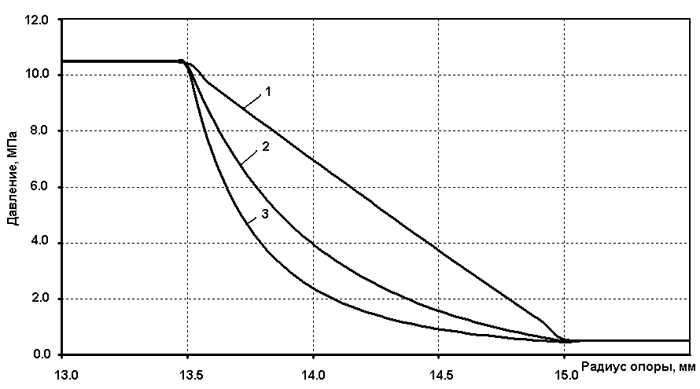
Рис. 9. Зависимость давления от угла деформации рабочей поверхности гидростатической опоры: 1 — без деформации; 2 — при деформации 0,25°; 3 — при деформации 0,5°
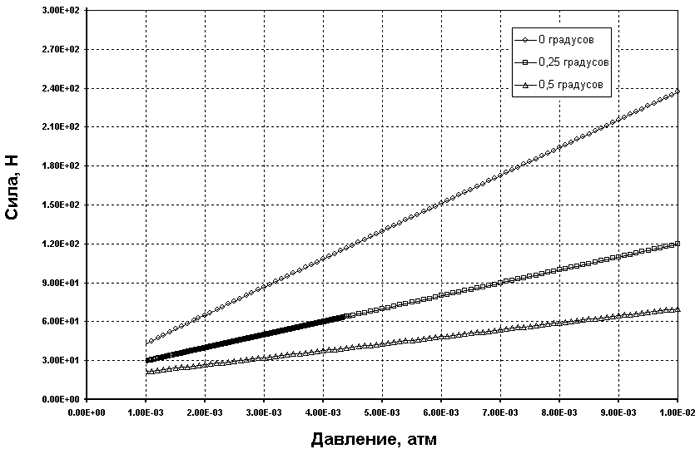
Рис. 10. Зависимость отжимающей силы на разгрузочном пояске ГСО от давления в поршневой камере АПГМ
Гидростатическая опора пытается автоматически компенсировать возникшую разницу между прижимающей и отжимающей силами путем уменьшения рабочего зазора. Но возможности по автокомпенсации у опоры ограничены, и при дальнейшем росте давления наступает момент, когда нарушается функционирование опоры — зазор становится равным нулю. Если жесткая гидростатическая опора имеет момент самостабилизации от перекоса, то по мере деформации опорной втулки этот момент меняет свой знак. В итоге это может привести к появлению одностороннего металлического контакта втулки с наклонным диском.
Моделирование рабочего процесса ГСО показало, что уровень давления не отражается на форме эпюры. То же самое можно сказать и о ширине уплотняющего пояска ГСО (рис. 10).
Таким образом, современные методы автоматизированного компьютерного проектирования при применении специализированного программного обеспечения в рамках методики виртуальной разработки и сопровождения изделий позволяют выявлять качественно новые возможности для улучшения рабочих характеристик как серийно выпускаемых, так и вновь разрабатываемых гидромашин.
Демо-версии программных продуктов можно заказать в «Русской Промышленной Компании».
Информация о программе, ценах, семинарах и курсах обучения, а также о специальных акциях — на www.cad.ru.


