Расчет корпусов химических аппаратов сложной формы
Постановка задачи, сценарий прочностного расчета и анализа результатов расчета
Оптимизация конструкции обечайки
В современных условиях химическое машиностроение является одной из наиболее бурно развивающихся отраслей машиностроения. Конструкции химических аппаратов становятся все более сложными, и на первый план выходит задача их расчета на прочность. Грамотно проведенный прочностной расчет позволяет снизить материалоемкость выпускаемой продукции, а следовательно, и ее стоимость.
В связи с интенсивным развитием химической промышленности в целом и нефтехимической в частности проблемы комплексного расчетного анализа элементов химических аппаратов и узлов приобретают особую актуальность.
В данной статье исследуется вопрос повышения точности расчетов на прочность, устойчивость и колебания химических реакционных емкостных аппаратов путем рассмотрения корпуса аппарата как единой системы с учетом присутствия люков, штуцеров, фланцев, опор и привода.
Проводить прочностной расчет подобных конструкций можно одним из двух методов: аналитическим, применяемым при так называемом ручном расчете, и численным, при котором используются методы приближенного решения задач прочности с помощью вычислительных средств.
Аналитические методы расчета корпусов химических аппаратов основаны на расчетных моделях гладких оболочек. При этом на прочность и устойчивость рассчитываются как отдельные элементы обечайка, крышка и днище аппарата [1, 2].
Из имеющегося многообразия вычислительных средств мы остановились на модуле прочностного анализа APM Structure3D, входящем в состав системы APM WinMachine совместно с препроцессором создания моделей для конечно-элементного анализа APM Studio. В APM Structure3D реализован метод конечных элементов, позволяющий получать исчерпывающую информацию о поведении рассчитываемой конструкции.
Прежде чем начать широкое внедрение APM Structure3D, необходимо было определить его потенциальные возможности с целью выявления целесообразности использования этого инструмента для нужд нефтехимической и газовой промышленности. Оценка точности вычислений производилась путем сравнительных параллельных расчетов, а возможности выявлялись при решении ряда практических задач.
Постановка задачи, сценарий прочностного расчета и анализа результатов расчета
В качестве примера был рассмотрен реакционный аппарат (рис. 1), состоящий из корпуса сложной формы и устройства перемешивания с приводом. В нашем примере рассматривается аппарат с дном в виде конической поверхности с углом при вершине конуса 45°. Объектом расчета является корпус со следующими параметрами:
• диаметр обечайки (d) — 2000 мм;
• высота обечайки (L) — 1800 мм;
• соотношение полуосей эллиптической крышки — 1:2;
• диаметр фланца (dф) — 2174 мм;
• толщина фланца (h) — 135 мм;
• диаметр люка (dл) — 400 мм.
Модель корпуса аппарата создавалась как поверхностная в 3D-редакторе модуля APM Studio. Вначале строилась гладкая оболочка (рис. 2), которая постепенно усложнялась: оболочка с фланцем; оболочка с фланцем и люком; оболочка с фланцем, люком и опорами-лапами (рис. 3). Корпус реакционного аппарата закреплялся шарнирно с помощью четырех опор-лап. Далее производился расчет на прочность, устойчивость и собственные частоты в модуле APM Structure3D. Источником внешних колебаний являлось вращение механического перемешивающего устройства.
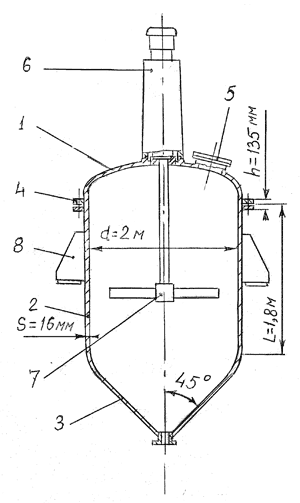
Рис. 1. Схема конструкции химического реакционного емкостного аппарата. Корпус состоит из эллиптической крышки (1), цилиндрической обечайки (2) и днища (3) конической или эллиптической формы. Крышка соединяется с обечайкой при помощи фланца (4) и имеет люк-лаз (5). Сверху на аппарат монтируется мотор-привод (6) для вращения мешалки (7). Аппарат крепится к стойкам основания с помощью четырех опор-лап (8)
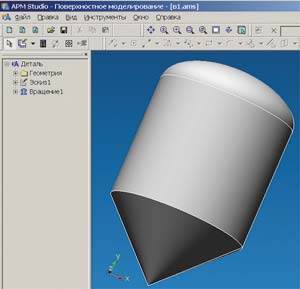
Рис. 2. Гладкая поверхностная модель корпуса аппарата, построенная в модуле APM Studio
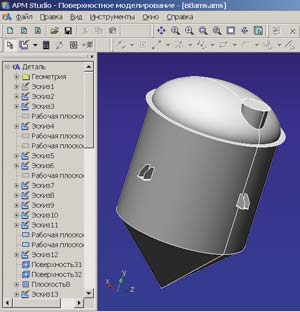
Рис. 3. Поверхностная модель корпуса реакционного аппарата с фланцем, люком и опорами-лапами, выполненная в модуле APM Studio
Анализ производился путем сопоставления результатов расчета модели корпуса, полученных с помощью модуля APM Structure3D, с результатами теоретического расчета. Подчеркнем, что подобное сравнение можно провести только для гладкой модели (см. рис. 2). Для более сложных моделей получить значения коэффициентов концентрации напряжений на сложных участках весьма проблематично.
Прочностной расчет
Для выполнения прочностного расчета корпуса необходимо вначале сгенерировать конечно-элементную сетку (КЭС) с определенным значением максимальной длины стороны конечного элемента (шаг разбиения), а затем передать ее в модуль APM Structure3D. В зависимости от величины шага разбиения конструкция в автоматическом режиме подвергается разбиению на определенное число конечных элементов. На рис. 4 приведена полученная КЭС упрощенной гладкой модели, результаты расчета которой использовались для сравнения с теоретическими результатами. На рис. 5 показана КЭС окончательной модели корпуса с фланцем и люком.
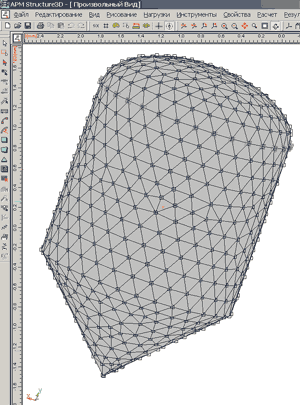
Рис. 4. Конечно-элементная сетка, сгенерированная на гладкой модели корпуса после передачи ее в модуль прочностного расчета APM Structure3D
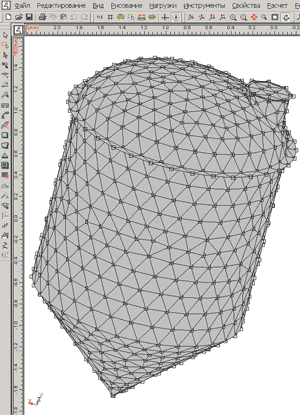
Рис. 5. Конечно-элементная сетка, сгенерированная на модели корпуса с фланцем и люком
После построения модели и разбиения ее на конечные элементы был проведен статический расчет модели корпуса, а также расчет на устойчивость.
Статический расчет
Статический расчет выполнялся исходя из того, что толщина стенки стального корпуса — 16 мм, а перепад внешнего давления составляет 1 МПа. Результаты статического расчета (а именно карта эквивалентных напряжений) приведены на рис. 6, а на рис. 7 представлены результаты расчета модели корпуса на устойчивость: коэффициент запаса по устойчивости и форма потери устойчивости.
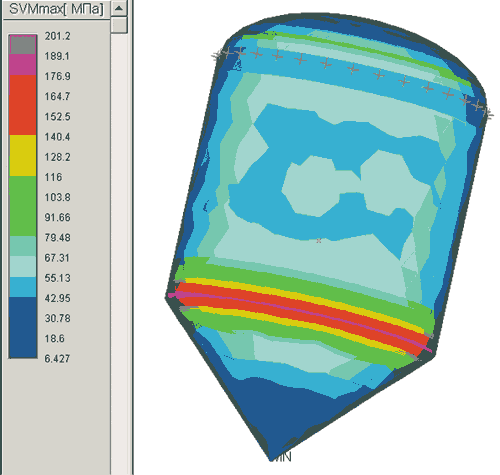
Рис. 6. Карта эквивалентных напряжений, полученная после расчета гладкой модели корпуса
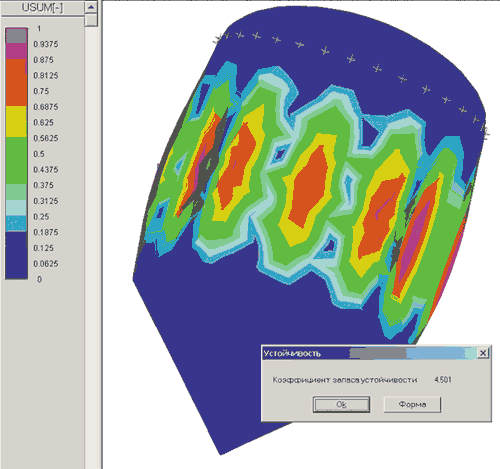
Рис. 7. Результаты расчета корпуса химического аппарата на устойчивость: значение коэффициента запаса по устойчивости и форма потери устойчивости
Результат конечно-элементного анализа любой конструкции (величина напряжений и параметры устойчивости) в значительной степени зависит от количества использованных при расчете конечных элементов разбиения. После того как количество элементов разбиения достигнет определенного уровня, результат будет близок к теоретическому значению. Справедливости ради следует отметить, что необходимое количество элементов разбиения, в свою очередь, очень сильно зависит от их типа (стержневые, пластинчатые или объемные), конкретного вида конструкции, ее нагружения, а также от возможной формы потери устойчивости.
В рассматриваемом примере был произведен расчет коэффициента запаса устойчивости гладкой модели с разным шагом разбиения (различным количеством конечных элементов). На рис. 8 представлена полученная зависимость коэффициента запаса по устойчивости от числа конечных элементов (кривая 1). Из анализа этой кривой видно, что если число конечных элементов превышает 2000, то значение коэффициента запаса устойчивости почти не меняется. Это может служить показателем оптимальности разбиения на конечные элементы. При количестве конечных элементов 3576 (максимальная сторона конечного элемента равна 125 мм) коэффициент запаса устойчивости имеет значение 2,181.
Увеличение количества конечных элементов до 4000 и более (пунктирный участок кривой 1) не дает каких-либо улучшений в плане точности расчетов, однако приводит к значительному возрастанию времени выполнения расчета компьютером (при решении этой задачи использовался компьютер с процессором Pentium 4, тактовой частотой 2000 МГц и оперативной памятью 512 Мбайт).
Аналитический расчет запаса устойчивости данного корпуса, произведенный по известным методикам [1, 2], дал значение запаса устойчивости (кривая 2 на рис. 8). Такое приближение к результату численного расчета говорит о том, что аналитический расчет дает несколько заниженные значения коэффициента запаса по устойчивости корпусов химического аппарата.
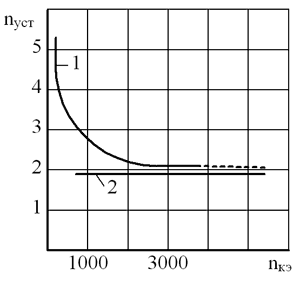
Рис. 8. Зависимость коэффициента запаса устойчивости пУСТ от числа конечных элементов пКЭ по результатам расчета в модуле APM Structure3D (кривая 1) и аналитического значения (кривая 2)
Следует отметить, что предложенные для аналитического расчета формулы, полученные на упрощенных моделях, лишь приближенно оценивают влияние крышки и днища на устойчивость обечайки корпуса химического аппарата. Использование численного метода решения систем уравнений методом конечных элементов в модуле APM Structure3D позволяет рассчитывать конструкцию в целом, без упрощений, причем с гораздо более высокой точностью, чем при аналитическом расчете.
Расчет на устойчивость
Дальнейшие расчеты на устойчивость и прочность данного типоразмера гладкого корпуса аппарата (см. рис. 1) были проведены для режима работы Рнар = 0,4 МПа и внутреннего избыточного давления Рвн = 0,8 МПа.
Толщина стенки корпуса определялась по известным аналитическим методикам и составила 11,8 мм при расчетном напряжении 123 МПа. Запас устойчивости при этой толщине из аналитического расчета после уточняющих итераций составил nуст = 2,24. Расчет коэффициента запаса по устойчивости, выполненный с использованием модуля APM Structure3D, показал несколько большее значение этого коэффициента, а именно nуст = 2,26 (при количестве конечных элементов nкэ = 1804).
Расчет на устойчивость корпуса аппарата с учетом фланца (см. рис. 1), выполненный в модуле APM Structure3D, показал увеличение запаса устойчивости (nуст) c 2,26 до 2,2653.
Дополнительное введение в корпус аппарата люка, в свою очередь, также повысило коэффициент запаса устойчивости до 2,861 (nкэ = 2000).
Оптимизация конструкции обечайки
При воздействии внутреннего избыточного давления напряжение в обечайке, рассчитанное по безмоментной теории Лапласа, составило 68,2 МПа. Расчет напряжений в модуле APM Structure3D, выполненный при той же геометрии расчетной модели и параметрах нагружения, показал уровень напряжения в средней части обечайки порядка 60-70 МПа (см. рис. 6).
Достоинством метода конечных элементов является возможность определения краевых напряжений в зоне перехода цилиндрической обечайки в коническое или эллиптическое днище. По результатам статического расчета была построена эпюра напряжений, возникающих в корпусе аппарата в зависимости от его меридиональной координаты. На рис. 9 показана эпюра изменения напряжений в первоначальной конструкции корпуса. Если в середине обечайки напряжения в два раза меньше допустимых, составляющих порядка 123 МПа, то в зоне перехода цилиндра в конус они намного превышают допустимые и достигают почти 200 МПа. Для уменьшения краевых напряжений был сделан утолщенный участок перехода от конуса к цилиндру (рис. 10) [2]. В данном расчете толщина переходного участка составила 25 мм. Расчеты показали снижение напряжений в зоне перехода цилиндра в конус с 200 до 20-30 МПа.
Исследование влияния условий закрепления в опорах-лапах показало, что жесткая заделка вызывает повышенные напряжения в этих зонах. Значительно снизить концентрацию напряжений в опорах позволяет шарнирно-подвижное опирание.
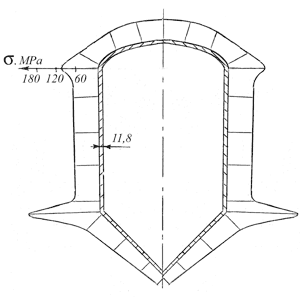
Рис. 9. Эпюры напряжений, возникающих в модели гладкого корпуса постоянной толщины в зависимости от меридиональной координаты
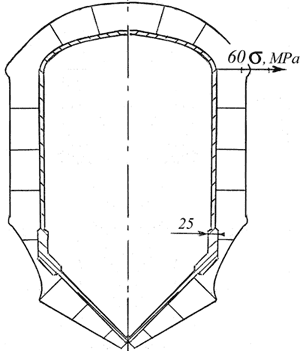
Рис. 10. Эпюры напряжений в модели корпуса с утолщением в зоне соединения обечайки с коническим днищем в меридиональном сечении
Выводы
Прочностной расчет корпусов химических аппаратов в модуле APM Structure3D необходимо предварять расчетом шага разбиения корпуса (минимально допустимое число элементов сетки разбиения), при котором целевые параметры, такие как коэффициент запаса устойчивости и величины напряжений, становятся постоянными.
При таких параметрах разбиения модуль прочностного расчета APM Structure3D дает очень близкое соответствие результатов по сравнению с известными аналитическими решениями. Отсюда можно сделать вывод, что этот программный продукт может быть рекомендован для всего комплекса расчетов химических аппаратов и трубопроводных систем любой степени сложности.
Уточненный расчет величины напряжений, коэффициентов запаса устойчивости с учетом сложности формы химических аппаратов в модуле APM Structure3D позволяет снизить металлоемкость конструкций.
Литература
1. Вихман Г.Л., Круглов С.А. Основы конструирования аппаратов и машин нефтеперерабатывающих заводов. М.: Машиностроение, 1978. 328 с.
2. Лащинский А.А. Конструирование сварных химических аппаратов: Справочник. Л.: Машиностроение, 1981. 382 с.
Владимир Васильев Канд. техн. наук, доцент кафедры «Горная и прикладная механика» Уфимского государственного нефтяного технического университета. |


