Применение программного комплекса FlowVision для моделирования режимов глиссирования самолета-амфибии
Традиционно обоснование внешних обводов самолета-амфибии делается на основе большого объема теоретических расчетов и экспериментальных исследований на моделях в аэродинамических трубах, гидроканалах и на открытой воде. Исследования аэро- и гидродинамики на экспериментальных моделях — достаточно длительный и дорогостоящий процесс, имеющий ряд ограничений, связанных с подобием модели и натурного объекта.
Прогресс вычислительной техники и численных методов расчета сделал доступным для использования в проектировании гидросамолетов программ численного моделирования процесса глиссирования, обтекания корпусов сложных геометрических форм, среди которых достойное место занимает российский программный комплекс FlowVision.
Реализованные в этом комплексе возможности применяются для постановки и решения задачи глиссирования модели самолета-амфибии Бе-200. Разработанные расчетные модели позволили провести систематические расчеты по моделированию глиссирования лодки гидросамолета во всем диапазоне взлетно-посадочных скоростей с учетом степеней свободы модели по всплытию и углу тангажа. Проведено сравнение полученных результатов с испытаниями физической модели в гидроканале филиала ЦАГИ. Получено хорошее соответствие результатов моделирования и эксперимента на картине как обтекания, так и зависимости физических величин от скорости глиссирования.
Расчеты глиссирования модели самолета-амфибии Бе-200 выполнялись совместно специалистами ОАО «ТАНТК им. Г.М.Бериева» и ООО «ТЕСИС». Первое представление результатов состоялось на 6-й Научной конференции по гидроавиации в г.Геленджике и вошло в сборник докладов «Гидроавиасалон-2006».
Постановка задачи
Изначально преследовалаcь цель разработать расчетную модель для определения гидродинамических характеристик (сопротивление и траекторные параметры движения) модели корпуса лодки самолета-амфибии в режимах глиссирования во всем диапазоне взлетно-посадочных скоростей. Проведенные исследования показали, что созданная в ходе работ модель позволила не только выполнить поставленную задачу, но и получить исчерпывающую информацию по характеру обтекания, включая волнообразование, а также по распределению гидродинамических нагрузок на элементах конструкции корпуса лодки в широком диапазоне скоростей глиссирования.
В плане вычислительной гидродинамики задача глиссирования корпуса гидросамолета имеет ряд особенностей, усложняющих численное моделирование (рис. 1). К ним относятся определение свободной поверхности (граница раздела вода — воздух) с учетом волнообразования, которое зависит от скорости движения и посадки на воду корпуса гидросамолета; установление пространственного положения самого гидросамолета относительно воды и свободной поверхности, определяемого действием сил и моментов, в том числе гидродинамической природы.
Важным достоинством FlowVision в подходе к решению подобных задач является возможность моделирования глиссирования корпуса гидросамолета с заданными степенями свободы. FlowVision позволяет находить не только силы и моменты, действующие на гидросамолет, но и параметры его балансировки по углу тангажа и всплытию под действием силы тяжести, а также гидродинамических сил и моментов.
При этом, в отличие от распространенного способа решения таких задач с использованием криволинейной лагранжевой расчетной сетки, отслеживающей движение тела и свободной поверхности, FlowVision использует альтернативный подход — расчет на неподвижной эйлеровой расчетной сетке. Этот подход позволил уйти от перегенерации расчетной сетки во всей области расчета на каждом шаге интегрирования по времени, для чего, как известно, необходимы значительные вычислительные затраты, а следовательно, большая вычислительная мощность компьютера. Известно, что задачи динамики движения тел с использованием перестраиваемой лагранжевой расчетной сетки обычно решаются на высокопроизводительных многопроцессорных вычислительных системах. Для нашего случая вполне хватило однопроцессорного персонального компьютера.
Для расчета движения корпуса лодки гидросамолета относительно неподвижной эйлеровой сетки с целью определения ее траекторных параметров (всплытие и угол тангажа) в FlowVision используется неявный метод. Для расчета движения свободной поверхности (граница раздела вода — воздух) с учетом волнообразования используется усовершенствованный метод VOF, который, по сравнению с известным традиционным методом VOF Хирта и Николса, не требует экстраполяции решения в ячейки около свободной поверхности, что позволяет повысить точность аппроксимации для этих ячеек. Это крайне важно для задач, где точность определения гидродинамических сил и моментов однозначно связана с точностью представления волновой системы.
В настоящей работе основное внимание уделялось моделированию гидродинамических сил и моментов и их влиянию на положение корпуса самолета-амфибии, поэтому аэродинамика гидросамолета учитывалась введением внешних сил и моментов, связанных со скоростью движения модели, поскольку это делалось при проведении соответствующих физических испытаний модели в гидроканале филиала ЦАГИ.
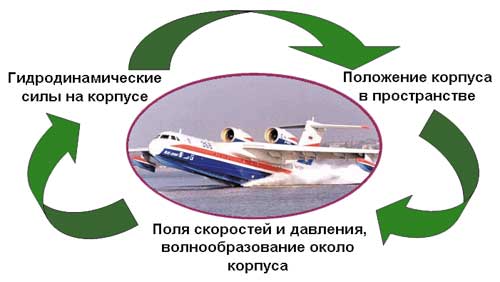
Рис. 1. Особенности постановки задачи
Расчетная модель
Модель движения жидкости
С учетом вышесказанного для определения движения свободной поверхности (границы раздела вода — воздух) математическая модель движения жидкости рассматривалась в приближении несжимаемой жидкости, состоящей из закона сохранения массы, уравнений Навье-Стокса, k-ε-модели турбулентности и метода VOF. Решение указанного набора уравнений в программном комплексе FlowVision представлено в модели «Свободная поверхность» (рис. 2 и 3).
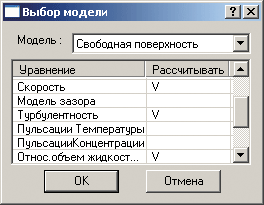
Рис. 2. Модель движения жидкости
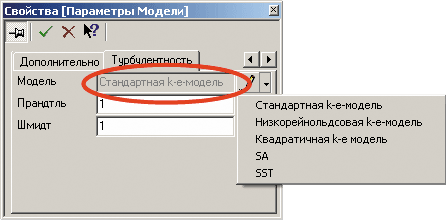
Рис. 3. Модель турбулентности
Модель движения самолета-амфибии
Математическая модель динамики движения корпуса лодки самолета-амфибии как твердого тела представлена в модуле «Подвижное тело». В данном модуле предусмотрена возможность задания массово-инерционных характеристик модели (рис. 4), положения Ц.М. (рис. 5), степеней свободы по всплытию и углу тангажа, а также внешних сил и моментов, которые обусловлены как аэродинамической разгрузкой, так и работающими двигателями (рис. 6 и 7).
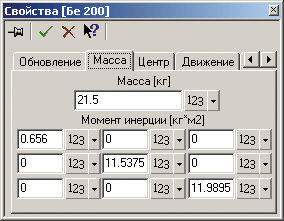
Рис. 4. Массово-инерционные характеристики модели
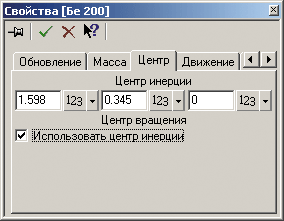
Рис. 5. Положение Ц.М. модели
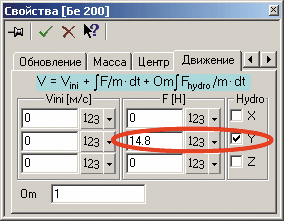
Рис. 6. Задание аэродинамической разгрузки и степени свободы по всплытию
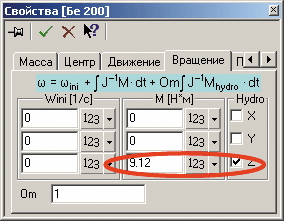
Рис. 7. Задание момента от двигателя и степени свободы по углу тангажа
Расчетная область и граничные условия
Расчетная область показана на рис. 8. В силу симметрии задачи, обусловленной анализом движения в продольной плоскости без скольжения и крена, рассматривалась только половина корпуса гидросамолета. Геометрические размеры расчетной области (длина, ширина, глубина, занимаемая водой) выбирались исходя из удовлетворения нижеописанным граничным условиям.
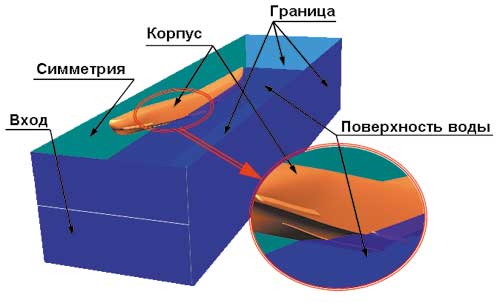
Рис. 8. Расчетная область и граничные условия
При построении расчетной модели были использованы следующие граничные условия:
- граница «Вход» — втекание воды в расчетную область:
V|w = Va;
k|w = 0,0025x(Va)2;
ε|w = Cμ(k|w.) 3/2/l
где Va — скорость лодки,
l ≈ 0,01 ÷ 0,1L;
где L — ширина корпуса гидросамолета;
- границы «Выход» и «Сторона» — задавалось граничное условие по давлению, соответствующее невозмущенному гидростатическому давлению. Для всех остальных переменных задавалось:
df /dn|w = 0.
Отметим, что граничное условие «Сторона» задавалось также и на «дне» расчетной области;
- граница «Симметрия» — это непротекание и проскальзывание для скорости, условие симметрии для всех переменных;
- «Корпус» — на корпусе гидросамолета ставилось граничное условие непротекания для нормального компонента скорости. Для касательного компонента, для k и e ставилось граничное условие через логарифмические функции.
- «Поверхность воды» — на свободной поверхности для всех величин, включая компоненты скорости, задавалось граничное условие:
df/dn|w =0.
Граничное условие для давления при этом, имело вид:
P|w = 0.
Численный метод
Метод конечных объемов
Программный комплекс FlowVision использует метод конечных объ емов. Уравнения движения жидкости аппроксимируются на прямоугольной расчетной сетке с локальной динамической адаптацией и подсеточным разрешением геометрии (рис. 9).

Рис. 9. Фрагмент прямоугольной расчетной сетки с локальной адаптацией и подсеточным разрешением геометрии
Уточним ряд приведенных ранее определений. Расчетная сетка, через ячейки которой не проходит поверхность расчетной области, имеет ячейки в виде параллелепипедов. Если через ячейку пролегает поверхность расчетной области, то ячейка обрезается этой поверхностью, превращаясь в сложный многогранник. Каждая ячейка может быть разбита (адаптирована) на восемь более мелких ячеек в зависимости от различных критериев адаптации (например, от градиента скорости).
В основе построения расчетных моделей для исследования глиссирования корпуса лодки самолета-амфибии была использована единая начальная расчетная сетка (рис. 10).
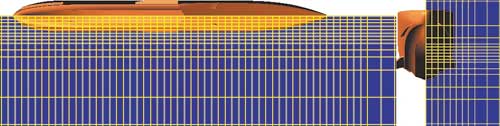
Рис. 10. Фрагмент начальной расчетной сетки
В дальнейшем для каждого варианта расчета по скорости глиссирования, в зависимости от характера обтекания модели и волнообразования, а также всплытия и угла дифферента, проводилась динамическая адаптация по объему определенных областей около корпуса лодки. В качестве примера на рис. 11 приведена конечная расчетная сетка для скорости движения модели, соответствующей «горбу сопротивления».

Рис. 11. Фрагмент конечной расчетной сетки
Адаптация сетки в этом случае была проведена по объему от пересечения водой редана до кормовой оконечности корпуса лодки модели гидросамолета на всю ширину корпуса, что соответствует области наиболее интенсивного изменения давления.
В заключение отметим, что в программном комплексе FlowVision уравнения Навье-Стокса решаются методом расщепления с расширением этого метода на случай неявной расчетной схемы. Для аппроксимации уравнений переноса используется схема высокого порядка точности.
Аппроксимация свободной поверхности
Как уже говорилось, программный комплекс FlowVision использует метод объема жидкости в ячейке (VOF) для аппроксимации свободной поверхности. Как известно, моделирование потоков со свободной поверхностью с использованием метода VOF разделяется на две задачи: первая — это перенос самого VOF, а вторая — аппроксимация уравнений движения в области около свободной поверхности.
Перенос VOF в программном комплексе FlowVision рассчитывается с помощью схемы с отрицательной диффузией, которая позволяет рассчитывать VOF без «размазывания» ее фронта. Метод аппроксимации свободной поверхности заключается в реконструкции свободной поверхности внутри поверхностных ячеек с использованием метода подсеточного разрешения.
Результаты
Проведенные систематические расчеты по определению картины течения около корпуса лодки самолета-амфибии на различных скоростях глиссирования показали качественное соответствие с картиной течения и волнообразования, наблюдаемой в физическом эксперименте.
На рис. 12, 13 и 14 приведены результаты расчета течения, волнообразования и распределения давления как около корпуса, так и на элементах его конструкции на различных скоростях глиссирования корпуса лодки модели самолета-амфибии.

Рис. 12. Волнообразование, граница раздела сред, положение корпуса и распределение давления вблизи раздела сред на скорости глиссирования 4,8 м/с

Рис. 13. Волнообразование, граница раздела сред, положение корпуса и распределение давления в области редана модели на скорости глиссирования 6,0 м/с, соответствующей «горбу сопротивления»
Из приведенных рисунков видно, что зависимость волнообразования от скорости глиссирования характеризуется возрастанием интенсивности волн около корпуса лодки и особенно позади него до скоростей «горба» сопротивления с последующим их уменьшением.
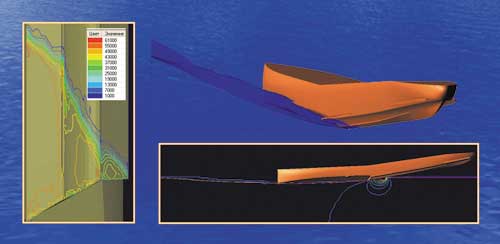
Рис. 14. Волнообразование, граница раздела сред, положение корпуса и распределение давления по днищу модели на предотрывной скорости глиссирования 11,1 м/с
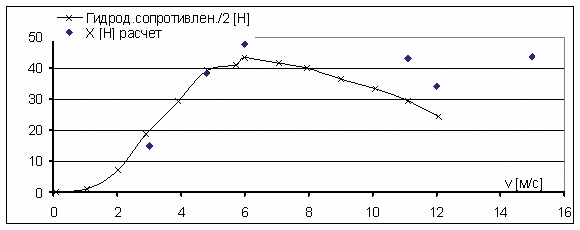
Рис. 15. Зависимость силы сопротивления корпуса лодки от скорости глиссирования
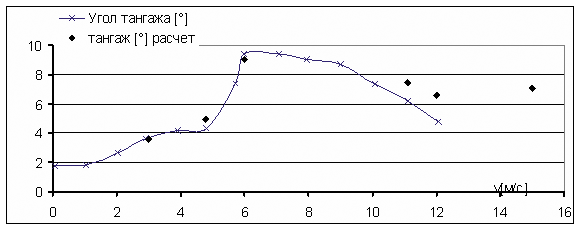
Рис. 16. Зависимость угла тангажа корпуса лодки от скорости глиссирования
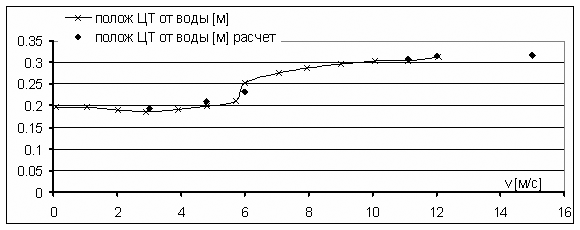
Рис. 17. Зависимость всплытия корпуса лодки от скорости глиссирования
Одновременно с ростом интенсивности волн наблюдается увеличение силы сопротивления (рис. 15), угла тангажа (рис. 16) и всплытия модели (рис. 17). Характерно, что основное изменение угла тангажа и всплытия происходит при небольшом интервале изменения скорости глиссирования — от 5 до 6 м/с. Это говорит о том, что на этом скоростном интервале резко увеличиваются гидродинамическая составляющая подъемной силы и гидродинамический продольный момент. Последующее увеличение скорости глиссирования приводит к плавному уменьшению угла тангажа (см. рис. 16) вследствие уменьшения гидродинамического момента. Увеличение всплытия (см. рис. 17) модели также происходит плавно. Снижение силы сопротивления на скоростях более 6 м/с обусловлено совокупностью перечисленных факторов: сокращением площади смоченной поверхности редана из-за всплытия модели и уменьшением угла атаки клина, на котором происходит глиссирование.
Сравнение результатов расчетов по определению гидродинамического сопротивления и траекторных параметров модели (угол тангажа, положение Ц.М.) с результатами испытаний модели в гидроканале филиала ЦАГИ приведены на рис. 15-17. Как видно из приведенных материалов, результаты расчета имеют удовлетворительную сходимость с экспериментом. При этом на скоростях глиссирования меньше 11 м/с, включая режим движения с максимальным гидродинамическим сопротивлением («горб сопротивления»), расхождение с результатами испытаний модели в гидроканале ЦАГИ не превышает 5%.
Заключение
С помощью FlowVision достигнуты положительные результаты в постановке и решении задачи о глиссировании корпуса лодки гидросамолета Бе-200. В частности:
- в рамках программного комплекса FlowVision построены расчетные модели, позволившие провести исследование физических процессов при глиссировании корпуса лодки гидросамолета;
- проведены систематические расчеты по определению траекторных параметров движения (всплытие, угол тангажа), силы сопротивления, а также картины обтекания модели. Определены зависимости физических величин от скорости глиссирования;
- выполнено сравнение полученных результатов с результатами испытаний физической модели в гидроканале филиала ЦАГИ. Получено соответствие результатов моделирования и эксперимента по картине как обтекания, так и зависимости физических величин от скорости глиссирования;
- достигнутые положительные результаты показывают пригодность разработанного метода численного моделирования для решения широкого класса задач, связанных с глиссированием сложных по гидродинамическим обводам корпусов лодок.


