Новый метод моделирования задач параметрического проектирования. Все возможности вариационного подхода при эффективности иерархического

Алексей Ершов

Принцип действия метода остовного моделирования

Построение оптимального остовного дерева

Генерация сокращенной системы уравнений

Заключение

Как известно, параметризация является мощным инструментом создания и переиспользования моделей, позволяющим и конструировать модель с заданными характеристиками, и получать новую модель путем изменения параметров уже существующей модели. Такие возможности очень важны для конструкторов и других пользователей САПР, поскольку позволяют существенно сократить время разработки конечных продуктов. Существует два классических вида параметрического проектирования: более традиционный иерархический, основанный на истории создания модели, и более совершенный по спектру возможностей вариационный. В данной статье мы рассмотрим математический подход, сочетающий достоинства обоих методов проектирования и свободный от их недостатков.

При иерархическом проектировании определяющее значение имеет порядок создания элементов, точнее порядок их подчинения друг другу — иерархия, которая отражается в дереве построения модели. Элемент, для создания которого использовались любые части или характеристики другого элемента, считается подчиненным этому элементу. Любая такая параметрическая модель хранит историю своего создания и позволяет редактировать любой элемент этой истории посредством изменения параметров подчинения вышестоящему объекту.

Данный способ прост в реализации, но лишает пользователя многих возможностей, таких как размещение друг относительно друга двух объектов, уже вошедших в историю построения модели. Это оказывается невозможным в силу образования циклов зависимостей между элементами и разрушения древовидной иерархической структуры. Получается, что если в модели есть такие нетривиальные зависимости между элементами, то для ее описания нужен принципиально иной подход. Серьезным недостатком традиционного метода иерархического проектирования является также необходимость постоянно работать с полностью определенной геометрической моделью без внутренних степеней свободы, что ограничивает возможности ее редактирования.

На смену традиционному параметрическому подходу, основанному на истории построения модели, пришла концепция вариационного проектирования, которая заключается в выражении связей конструктивных элементов и определяющих их параметров посредством ограничений. Ограничение — это формальное декларативное описание произвольной связи между объектами модели, не предполагающее подчинение одного объекта другому. Обычно ограничения подразделяют на логические (параллельность прямых, касание плоскости и цилиндра) и параметрические (длина отрезка, радиус сферы, угол между гранями). Путем задания ограничений пользователь может полностью управлять формой проектируемого изделия, при этом ему не надо просчитывать взаимное расположение частей модели — САПР автоматически определяет положение всех объектов, которые разрешают все заданные пользователем ограничения.

Главное преимущество вариационного подхода по сравнению с подходом, основанным на истории построения, — значительно более высокие выразительные возможности системы. Конструктору не нужно полностью продумывать пошаговое создание изделия — за него это сделает компьютер. В любой момент можно добавить, удалить ограничения или поменять значения их параметров и получить новую модель с заданными свойствами. Более совершенный механизм описания геометрической модели позволяет иметь дело с циклическими зависимостями и не полностью определенными моделями.

Тем не менее вариационный подход иногда подвергается критике со стороны разработчиков систем традиционного параметрического проектирования. Как недостаток расценивается необходимость одновременного разрешения системы всех ограничений при изменении параметров модели. Таким образом, система вариационного проектирования может быть разработана только на основе специализированного геометрического решателя, а ее потенциально слабым звеном считается малое быстродействие при изменении модели пользователем.

Геометрические решатели LGS 2D и LGS 3D, разработанные в компании ЛЕДАС, внедрены в ряд отечественных САПР и позволяют эффективно решать задачи вариационного проектирования. Тем не менее некоторые пользователи хотя и были довольны новыми возможностями, предоставляемыми более современной концепцией, но отмечали снижение производительности при обработке некоторых моделей. С целью устранения этого недостатка компания ЛЕДАС разработала специальный метод моделирования задач вариационного проектирования и реализовала его в продукте LGS 3D.

При работе данного метода по геометрической модели с логическими и параметрическими ограничениями, записанной в виде графа, строится остовное дерево, вершинами которого являются все объекты, а дугами — некоторые ограничения, позволяющие эффективно параметризировать положение одних объектов по отношению к другим. Для вычисления конфигурации проектируемого изделия в этом случае необходимо решать не всю систему заданных ограничений, а лишь те из них, которые не попали в остовное дерево и «замыкают» собой циклы. Таким образом, происходит обсчет лишь тех ограничений, которые принципиально невозможно обработать с помощью иерархического подхода. Далее мы рассмотрим принцип действия этого нового метода.

Принцип действия метода остовного моделирования

В любом промышленном решателе задач вариационного проектирования набор геометрических ограничений рано или поздно превращается в систему нелинейных уравнений, которая решается с помощью специальных вычислительных методов. Основными переменными в такой системе уравнений являются либо новые координаты ее геометрических объектов, либо углы поворотов и компоненты векторов смещения, описывающие процесс перевода геометрических объектов в новое положение. Трехмерные геометрические объекты в САПР достаточно сложны и для их представления требуется целый набор элементарных объектов (точек, кривых, поверхностей), поэтому при моделировании они представляются твердыми телами — наборами элементарных объектов, которые не меняют положения относительно друг друга. Поэтому второй способ на практике оказывается более предпочтительным — вместо нахождения координат всех элементарных объектов ищутся так называемые трансформации тел вида (R | T), где R = Rα*Rβ*R — композиция матриц поворота на углы α, β, вокруг осей Ox, Oy, Oz, а T = (Tx,Ty, Tz)^T — вектор смещения вдоль этих осей. Ограничения, заданные пользователем, записываются как уравнения на искомые положения тел Xnew = R · Xold + T, таким образом, они выражаются через ротационные переменные α, β, и трансляционные x, y, z.

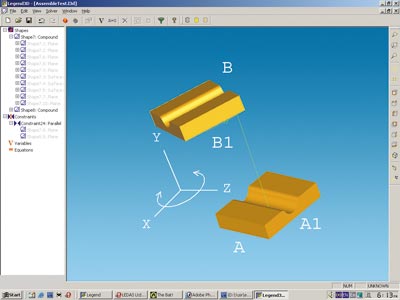
Идея нового метода остовного моделирования заключается в том, чтобы вместо полного набора из шести переменных α, β, , x, y, z использовать меньший набор, полностью параметризирующий все возможные положения тела по отношению к некоторому другому телу, с которым оно связано одним или несколькими ограничениями. Например, легко заметить, что если две детали A и R связаны ограничением параллельности граней A₁ и B₁ , то положение детали B можно описать с помощью всего четырех переменных. Действительно, при любом положении детали A деталь B должна быть расположена так, чтобы ее грань B₁ была параллельна грани A₁, значит, при этом ее можно лишь вращать вокруг общего перпендикуляра к плоскостям A₁ и B₁ и смещать в произвольном направлении. Таким образом, деталь B относительно детали A имеет одну ротационную и три трансляционные степени свободы (рис. 1).

Рис. 1. Взаимные степени свободы двух деталей

Формально описать положение B относительно A можно с помощью формулы Xb = L · Rβ · F · Xa + T , где L и F  — специальные матрицы, не включающие переменных, а Rβ  — матрица поворота вокруг оси Oy . Матрица F определяет движение детали A  — из исходного положения в так называемое каноническое положение, при котором ее грань A₁ перпендикулярна оси Oy , а матрица L определяет движение детали B из такого же канонического положения в исходное. Таким образом, при генерации уравнений в качестве переменных для тела, представляющего деталь A , используется полный набор из шести переменных a , β , , x, y, z , а для тела, представляющего деталь B,  — сокращенный набор из четырех переменных β , x, y, z .

Поступая таким же образом с другими телами модели, можно построить остовное дерево, в котором дуга «отец — сын» показывает, что возможные трансформации «сына» определяются относительно трансформаций «отца» по формуле Tson = (L · P( a , β , , x, y, z ) · F) ·Tfather, где L и F  — константные матрицы, а P ( a , β , , x, y, z )  — параметрическая трансформация, состоящая из матрицы поворота и вектора сдвига, где некоторые из переменных a , β , , x, y, z фиксированы благодаря учету ограничений между «отцом» и «сыном». Количество используемых для такого представления переменных уменьшается на число степеней свободы, которые снимают ограничения-дуги между «сыном» и «отцом». Количество уравнений тоже существенно снижается, поскольку ограничения, являющиеся дугами остовного дерева, уже учтены с помощью параметрической трансформации и не требуют генерации уравнений.

В общем случае при остовном моделировании задачи вариационного проектирования необходимо выполнить два шага: построение оптимального остовного дерева и генерацию сокращенной системы уравнений.

Построение оптимального остовного дерева

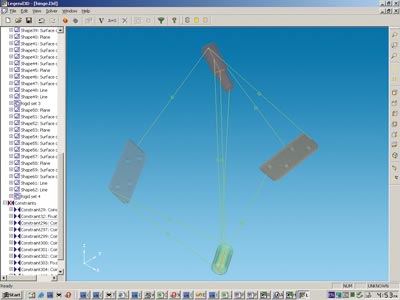
На первом шаге по графу объектов и ограничений строится мультиграф, вершинами которого являются геометрические тела, а ребрами — ограничения, которыми связаны объекты в этих телах (рис. 2). Каждое ребро мультиграфа помечается числом, равным количеству степеней свободы, снимаемому соответствующим ограничением. Например, совпадение плоскостей снимает три степени свободы, а расстояние между точкой и плоскостью — только одну.

Рис. 2. Исходная модель из четырех тел и девяти ограничений

Затем происходит анализ попарных взаимосвязей геометрических тел с учетом всех заданных между ними ограничений. Например, на рис. 3 для пары тел T₂ – T₄ требуется рассмотреть три ограничения, а для пары тел T₃ – T₄  — только одно. В процессе анализа происходит поиск в базе предопределенных шаблонов остовного моделирования, каждый из которых определяет для конкретного набора из одного-трех ограничений, какие из переменных β , β , , x, y, z трансформации одного из тел можно зафиксировать при позиционировании его по отношению к другому телу. Каждый шаблон обладает весом, равным сумме степеней свободы, снимаемых всеми входящими в него ограничениями. После проведения анализа мультиграф превращается в граф взаимосвязей тел: для каждой пары тел набор ребер-ограничений между ними заменяется одним ребром, которому приписывается вес, равный весу найденного шаблона.

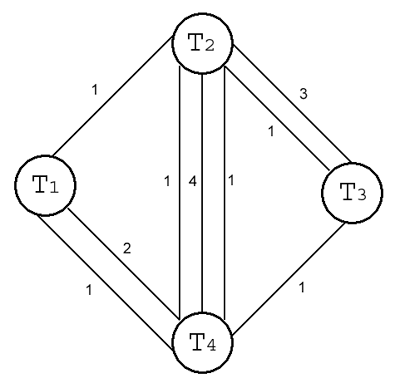
Рис. 3. Мультиграф с помеченными ребрами

Набор всех возможных шаблонов, описывающих взаимосвязи двух тел, хоть и объемен, но конечен; на практике же достаточно рассмотреть несколько десятков наиболее эффективных шаблонов схожей структуры. Если набор N ограничений между двумя телами не совпадает ни с каким из шаблонов, то в качестве результата выбирается шаблон, набор ограничений M которого является подмножеством N . Это означает, что при генерации системы уравнений ограничения из M не будут генерироваться, а ограничения из M / N будут обрабатываться обычным образом.

С целью минимизации количества переменных и уравнений в генерируемой системе уравнений необходимо найти в построенном графе взаимосвязей тел остовное дерево максимального суммарного веса. Это можно эффективно сделать, например, с помощью алгоритма Борувки за время O(nlog(n)) , где n  — число ограничений в модели. Для ограничений, которые вошли в шаблоны, включенные в построенное остовное дерево, уравнения генерировать не надо — такие ограничения автоматически выполнятся за счет механизма параметрических трансформаций. В результате система уравнений будет построена только для ограничений исходной модели, которые замыкают циклы в графе тел и ограничений, причем эта система уравнений будет иметь наименьшее возможное число переменных (рис. 4).

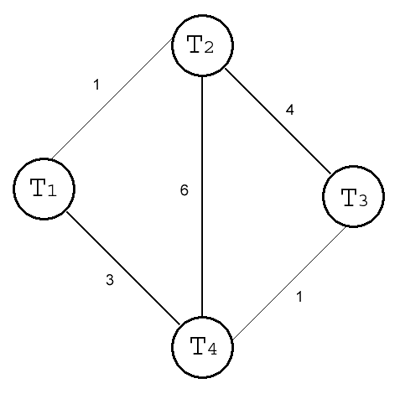
Рис. 4. Минимальное остовное дерево в помеченном графе

Генерация сокращенной системы уравнений

Корректная генерация уравнений для незадействованных ограничений требует создания объектов специального класса «уравнение на параметрические трансформации». Этот класс реализует для текущего значения переменных функции вычисления невязки уравнения и градиента этой невязки, необходимые для решения системы уравнений методом Ньютона. Текущие означивания переменных подставляются в параметрические трансформации, после чего происходит вычисление невязки и градиента.

Вычисление невязок и градиентов невязок таких уравнений гораздо сложнее, чем обычных, поскольку требуется выполнить столько операций умножения матриц 3x3, какова суммарная длина весов ребер, лежащих в остовном дереве на пути между телами, содержащими аргументы данного ограничения. Тем не менее если вычисления невязок и градиентов производить от корня дерева к его вершинам, используя при каждом новом вычислении результаты, полученные на предыдущем шаге, то общая сложность вычислений будет не более квадратичной. Поскольку при решении системы нелинейных уравнений методом Ньютона на каждой итерации самой трудоемкой операцией является кубическое по времени решение линейной системы уравнений, это усложнение значительно меньше эффекта ускорения из-за уменьшения размера системы уравнений.

Поскольку формула вычисления трансформаций «сына» через трансформации «отца» Tson = (L · P( α , β , , x, y, z ) · F) · Tfather требует определения константных матриц L и F , они аналитически вычисляются до генерации уравнений. Для примера рассмотрим простейший случай шаблона, содержащего только одно ограничение: пусть в остовное дерево попало ребро, связывающее два тела отношением «отец — сын». При построении трансформаций L и F в качестве координат объектов берем начальные, взятые с эскиза координаты (рис. 5).

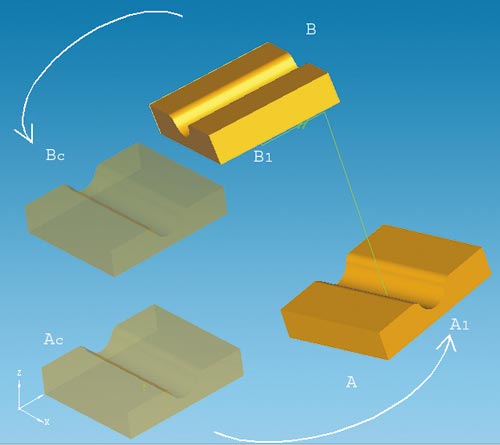
Рис. 5. Определение трансформаций тел

В любом теле в трехмерном пространстве можно ввести локальную систему координат, мы выберем локальную систему координат в теле-«отце» и теле-«сыне» так, чтобы объекты, непосредственно связанные ограничением, попавшим в остовное дерево, имели максимально простые координаты. Если таким объектом является точка, то целесообразно начало координат совместить с координатами этой точки, а если объект — это плоскость, прямая, кривая или поверхность, то начало координат совмещается с опорной точкой этих объектов. Направление оси Ox выбирается так, чтобы оно совпадало с направлением прямой, нормалью к плоскости, локальной координатной осью Ox кривой или поверхности. Трансформация F строится так, чтобы локальная система координат тела-«отца» перешла в глобальную систему координат, а трансформация L  — так, чтобы глобальная система координат перешла в локальную систему координат тела-«сына».

Заключение

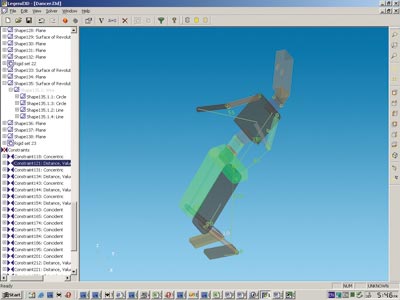
Тестовая база, используемая для оценки эффективности реализованного метода, включает 3120 тестов. В основном в нее входят тесты, сгенерированные по промышленным задачам, решаемым с помощью САПР. Средний по размерам тест содержит несколько десятков геометрических тел и около сотни ограничений между ними. Результаты сравнительного тестирования решателя LGS до и после реализации метода остовного моделирования показали, что полное время решения тестов сократилось в три раза (рис. 6).

Рис. 6. Модель с 22 ограничениями требует всего девять уравнений

Такой успех стал возможным из-за сочетания в новом методе остовного моделирования положительных качеств как методов параметрического проектирования, так и методов вариационного проектирования. Наряду с описанным подходом в решателе LGS используется большое количество других методов повышения производительности: различные виды геометрической декомпозиции, алгоритмы упрощения геометрических задач, техника ускорения решения нелинейных систем уравнений.

Все это позволяет c уверенностью заявить, что пользователи решателя LGS уже сейчас могут получить все возможности вариационного подхода при эффективности традиционного иерархического проектирования.

САПР и графика 9`2007