Автоматическое определение минимальных габаритов деталей
В практике машиностроительного проектирования и конструирования часто возникает задача определения минимальных габаритов деталей, сборок и агрегатов, в частности при вычислении размеров заготовок. Если для общемашиностроительных конструкций с небольшим количеством деталей это, как правило, не составляет труда, то для сложных сборок с тысячами конструктивных элементов с непростой пространственной геометрией, характерных, в частности, для авиа- и судостроения, решение такой задачи отнюдь не всегда является очевидным и сопряжено с большой трудоемкостью. Одним из проектов компании ЛЕДАС является разработка соответствующих приложений в среде для нескольких САПР из числа лидирующих на мировом рынке. При постановке задачи в промышленном масштабе большую роль сыграли консультации с ведущими техническими специалистами ОАО «Гражданские самолеты Сухого».
Задача определения габаритов трехмерных геометрических тел встречается во многих приложениях вычислительной геометрии, но ей обычно уделяется мало внимания. Между тем от качества определения габаритов зачастую зависит качество всего решения. Рассмотрим, например, задачу размещения плоских объектов на листе. Будем представлять сложную геометрию ограничивающим прямоугольником вдоль осей координат и размещать прямоугольники на плоскости листа. На рис. 1 представлены варианты размещения детали на листе для различных ограничивающих прямоугольников. Задача состоит в том, чтобы найти прямоугольник, имеющий минимальную площадь и объемлющий данную деталь. Габариты этого прямоугольника называются минимальными габаритами детали. При обобщении задачи на более интересный с практической точки зрения случай трехмерных тел будем говорить о габаритах минимального ограничивающего параллелепипеда (бокса).
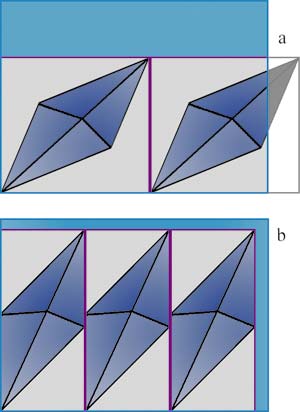
Рис. 1. Выбирая ограничивающий бокс вдоль осей (а), на листе можно поместить всего одну заготовку вместо трех, как в оптимальном случае (b)
Определение габаритов детали и ее заготовки — важная часть производственного процесса. Современные САПР-системы позволяют найти габариты, но только вдоль осей X, Y, Z, которые, как показано на приведенном выше примере, далеко не всегда составляют минимум функции объема ограничивающего параллелепипеда; в задачах раскроя неправильный выбор габаритов повлечет за собой перерасход материала. Естественно, инженер может повернуть систему координат и пересчитать габариты вдоль новых координатных оcей; продвинутый пользователь может написать скрипт для своей системы проектирования, который перебирает с некоторым шагом системы координат и находит конфигурацию, составляющую минимум объема ограничивающего параллелепипеда. Однако это не решает проблемы — инженер не может быть уверен, что нашел минимальные габариты заготовки, более того — невозможно оценить, во сколько раз найденные габариты отличаются от реальных.
В настоящее время опубликован ряд работ, посвященных проблеме вычисления габаритов для трехмерных полигональных сеток. Данная постановка может быть применена для решения общей задачи, поскольку современные САПР-системы предлагают встроенные алгоритмы тесселляции, позволяющие строить полигональные сетки по BRep-модели с заданной погрешностью. Несложное наблюдение, показывающее, что минимальные ограничивающие параллелепипеды полигональной сетки и ее выпуклой оболочки совпадают, позволяет ограничиться нахождением боксов выпуклых тел.
Среди современных работ заслуживают внимания эвристический метод вычисления габаритов вдоль осей инерции и точный метод нахождения бокса. Метод, определяющий бокс по осям инерции, обладает хорошими вычислительными характеристиками по требуемой памяти и времени выполнения, но, к сожалению, объем найденного им ограничивающего параллелепипеда может на порядок отличаться от объема минимального, что приведет к соответствующему перерасходу материала при производстве детали. Принимая во внимание тот факт, что стоимость вычислений на компьютере с каждым годом снижается и что уже сейчас на рынке доступны недорогие решения для параллельных вычислений, для реализации был выбран более дорогой в плане вычислений алгоритм нахождения точного минимального ограничивающего параллелепипеда.
Вкратце алгоритм нахождения точного минимального бокса заключается в следующем.
В процессе перебора всех пар ребер треугольной сетки положение ограничивающего параллелепипеда для каждой пары ребер определяется одной степенью свободы. Путем анализа геометрии сетки и поиска граничных точек определяются интервалы, на которых функция объема этого параллелепипеда описывается отношением тригонометрических полиномов. Для нахождения экстремумов этой функции на заданном интервале используется математическая библиотека, разработанная компанией ЛЕДАС. Сравнивая объемы в экстремумах, можно найти минимальный объем для заданной пары ребер, после чего взять минимум по всем парам ребер. Полученное число и соответствующая ему конфигурация бокса и будет решением задачи. Число ребер квадратично зависит от числа элементов в сетке; для каждой пары ребер с помощью ряда оптимизаций за линейное время можно найти решение, поэтому общая вычислительная сложность алгоритма получается кубической. С помощью методов аналитической геометрии можно доказать, что найденный алгоритмом ограничивающий параллелепипед будет минимальным для заданной полигональной сетки.
При реализации подхода учитывалась высокая вычислительная сложность алгоритма, поэтому был реализован ряд упрощений (в частности, избежание нахождения корней тригонометрического полинома, пропуск конфигураций, на которых минимум заведомо не может быть получен, и т.д.), позволяющих ускорить его работу при незначительном ухудшении качества результата. Также была предоставлена возможность задания пользователем вручную одного из направлений ограничивающего параллелограмма. Эта функциональность может быть востребована в производственных задачах, в которых ребра ограничивающего параллелепипеда должны быть параллельны/ортогональны одной из осей симметрии детали.
Описанный алгоритм нахождения точного минимального ограничивающего параллелепипеда допускает параллельную реализацию — решение для каждой пары ребер можно искать независимо от других и потом выбирать оптимальное. Учитывая существенный прогресс технологий в области доступных параллельных вычислений, в настоящее время рассматривается возможность реализации параллельной версии алгоритма, которая будет буквально в десятки раз быстрее однопоточного решения.
Разработанное решение LEDAS Geometrical Measurement (LGM) включает C++ API, удобное для программистов, работающих с Microsoft Visual C++; предоставляется также API для пользователей других компиляторов. Любой из предложенных API позволяет быстро интегрировать решение в практически любую САПР — для этого программист должен вызвать модуль тесселляции модели конкретной САПР и передать полученную треугольную сетку на вход модуля LGM. По этой схеме были созданы конечно-пользовательские компоненты для систем CATIA V5, а кроме того, в разработке находятся приложения в среде NX.
Рассмотрим типичный сценарий работы с компонентом LGM пользователя CATIA:
Пользователь выделяет одну или несколько моделей в сборке.
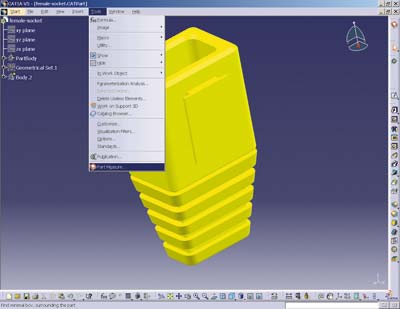
В меню Tools он выбирает LGMMeasure (рис. 2).
Рис. 2. Вызов приложения подсчета габаритов
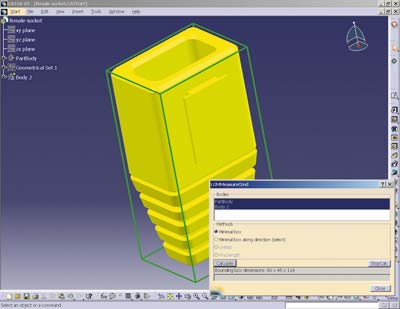
В появившемся диалоговом окне пользователь выбирает метод и инициирует процесс вычислений (скрин).
Результаты вычислений отобразятся в поле вывода и будут доступны для копирования в буфер обмена. Для визуальной проверки результата будет отображен найденный ограничивающий параллелепипед (рис. 3).
Рис. 3. Визуальное и цифровое представление габаритов выбранных тел
При настройке решения под нужды конкретного заказчика пользовательский интерфейс и API могут быть расширены, например LGM может передать пользователю параметры системы координат, оси которой совпадают с ребрами параллелепипеда.
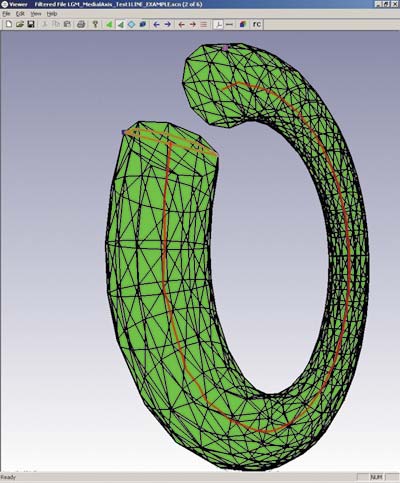
Рис. 4. Алгоритм нахождения длины профиля основан на размещении «скелета» внутри тела и измерении его длины
Стоит упомянуть и о специфическом варианте задачи, решавшейся в ходе разработки, — нахождение размеров заготовки в частном, но часто встречающемся на практике случае — для деталей, изготавливаемых из профильной заготовки (рис. 4). Подробнее о ней мы планируем рассказать в других публикациях.
Подводя итоги, можно сказать, что компания ЛЕДАС разработала наукоемкое решение, которое может найти применение в широком круге задач САПР и вычислительной геометрии. Благодаря наличию готовых компонентов вычисления минимальных габаритов для систем CATIA и NX, пользователи могут получить преимущества от их использования уже сегодня. В настоящее время разработанные приложения проходят стадию интенсивного окончательного тестирования на промышленных примерах, отладки и доводки пользовательского интерфейса. Более подробную информацию можно получить по адресу: info@ledas.com.