Обеспечение технологических измерений проушин в деталях каркаса авиационных конструкций
Одними из наиболее ответственных элементов деталей каркаса авиационных конструкций являются проушины (системы проушин c отверстиями), используемые для соединения агрегатов в общую конструкцию, присоединения отклоняемых элементов механизации, внешних подвесок и др. (рис. 1).

Рис. 1. Деталь авиационного каркаса
Традиционный контроль при проведении механической обработки осуществляется калибрами — пробками и профилированными штангами. Получаемая информация типа «годен — не годен», а для группы отверстий — «соосны — не соосны», как правило, не позволяет установить по этапам технологического процесса цифровые значения имеющихся отклонений, а также положение отверстий в системе осей детали. В полном объеме эта информация может быть получена с применением контрольно-измерительной машины при сопоставлении результатов измерений с исходными технологическими и конструкторскими моделями деталей. В ряде случаев она позволяет оперативно определить минимально необходимые доработки, включая корректировку управляющих программ, размеров инструмента, а также получить возможность использования запасов в допусках на другие линейные размеры детали при определенных отклонениях в позиционировании осей без доработки или переделки деталей.
В принципе, при использовании программируемых измерительных машин данные задачи решаются в штатном обеспечении, однако требуют разработки соответствующих управляющих программ измерений. Проведение измерений прерывает технологический процесс и требует перемещения детали на стол измерительной машины. Рациональным с этих позиций является использование координатно-измерительных машин (КИМ) типа манипулятор, допускающих установку непосредственно на технологических позициях. При управлении оператором вручную можно провести непосредственное измерение при любом положении детали и КИМ с базированием относительно математической модели в известном программном обеспечении (например, Power Inspect фирмы Delcam). Однако точность машин такого типа невысока.
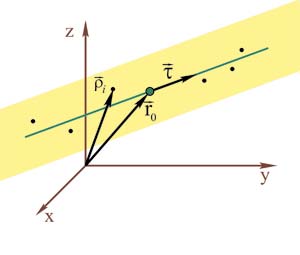
Рис. 2. Поиск положения прямой в пространстве
Для повышения точности определения параметров геометрических объектов, в принципе, можно использовать увеличенный объем замеров (число измеренных точек объекта — 100 и более). Минимально необходимый набор алгоритмов и программ статистической обработки материалов замеров большого объема для рассматриваемых деталей включает следующие геометрические элементы: ребра, грани, отверстия (плоский и пространственный случаи). Рассмотрим их последовательно.
Поиск ребер и граней в пространстве приводит к задачам о построении прямой и плоскости через массив точек. Прямая и плоскость представляются в векторно-параметрическом виде (рис. 2 и 3), что позволяет решить задачу для их произвольного положения в текущей системе координат, а также исключить вырождение решения.
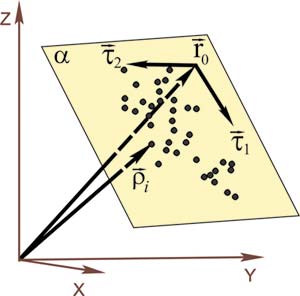
Рис. 3. Поиск геометрических параметров плоскости
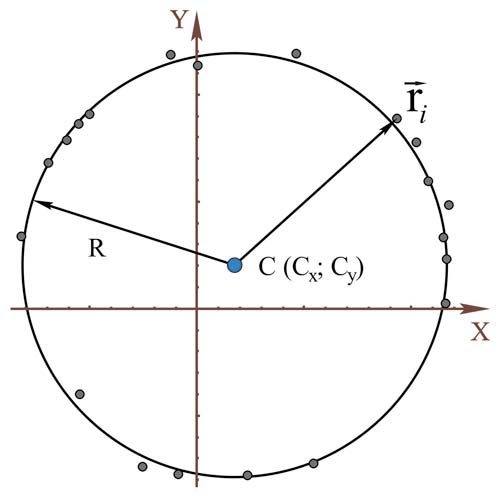
Рис. 4. Оценка параметров окружности
Получение параметров отверстия по замеру координат на плоскости сводится к задаче о построении окружности на массиве точек (рис. 4). В ней применение метода наименьших квадратов приводит к системе нелинейных уравнений. Введение линеаризации с малыми отклонениями от статистической оценки положения центра и радиуса для измеренного массива точек позволяет произвести поиск центра окружности и радиуса в быстро сходящемся итерационном процессе. Введены оценки для возможного неравномерного распределения замеренных точек по окружности, а также для оценки параметров дуг (скруглений) (рис. 5).
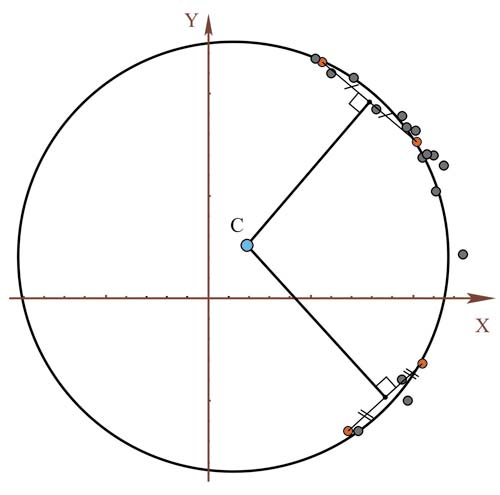
Рис. 5. Оценка параметров дуг (скруглений)
Пространственное положение отверстия определяется по параметрам цилиндра, построенного на материалах замера. Решение этой задачи базируется на предыдущих задачах с некоторой трансформацией алгоритмов. В результате по замеру пространственных точек, лежащих на поверхности обобщенного цилиндра, соответствующей внутренней поверхности отверстия, определяются его параметры — положение оси и радиус, наилучшие в смысле отклонения от исходных данных (рис. 6).
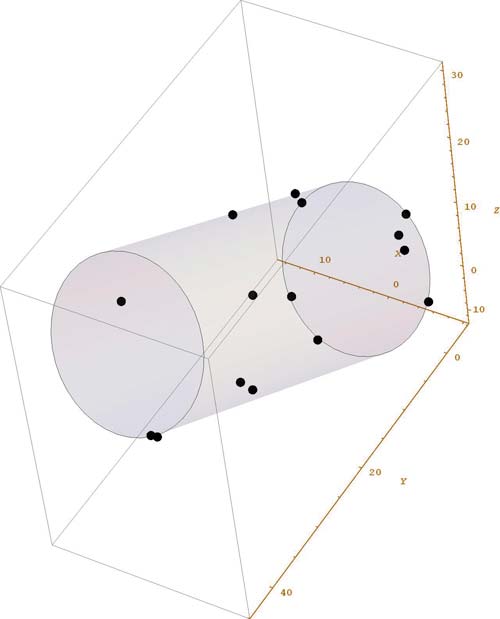
Рис. 6. Цилиндр на множестве точек
Еще одной практически важной решенной задачей является оценка максимального радиуса вала, который может войти в изготовленное отверстие, представленное точками замера. Ее решение отличается от оценки погрешностей изготовления по методу наименьших квадратов и является по существу минимаксным, то есть проводится поиск максимальной среди минимальных (для множества вписанных) окружностей. На рис. 7 показано сравнение решений, полученных методом наименьших квадратов и с использованием минимаксной оценки. Видно, что реальный радиус проходного вала может быть на 3-15% больше, чем его оценка традиционным статистическим методом. Практическим результатом данного решения становится оценка минимальных доработок для отверстий и валов. Соответственно могут быть уменьшены трудозатраты на их доработку.
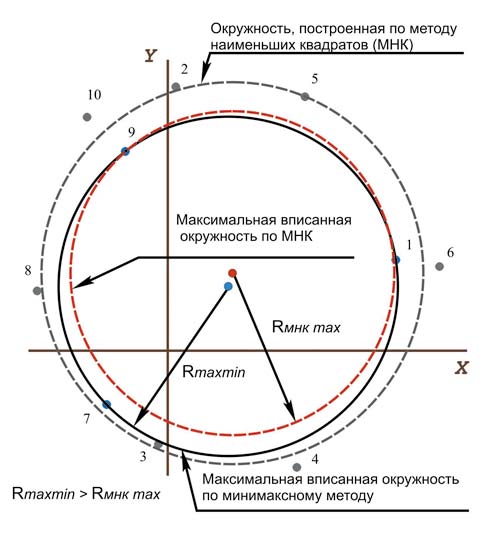
Рис. 7. Сравнение методов оценки вала максимального радиуса
Работа выполнена на базе механического производства ЗАО НПП «Завод полимерных и композитных конструкций» (www.zpkk.ru). Используемые КИМ — Romer Arm 2000, CimCore INFINITE. Программная реализация алгоритмов выполняется как приложение в комплексе системы геометрического моделирования и программирования станков с ЧПУ ГеММа-3D (www.gemma.ru).


