Принцип построения структурированной гексаэдрической сетки в ANSYS
Наши клиенты — пользователи программного обеспечения ANSYS часто спрашивают, в каких случаях требуется использование структурированной гексаэдрической сетки. Пользователи ANSYS знают, что подготовка полностью структурированной сетки очень трудна и для сложных криволинейных моделей требует в несколько раз больше времени по сравнению с неструктурированной сеткой. Поэтому возникает вполне закономерный вопрос: стоит ли тратить много времени на построение структурированной гексаэдрической сетки, если можно создать неструктурированную?
Пакет ANSYS имеет множество приложений практически для всех областей современной науки и техники. При этом следует учитывать, что различные физические задачи требуют разных подходов при моделировании и создании расчетной сетки. В рамках данной статьи будут рассмотрены некоторые особенности построения сетки для задач гидро- и газодинамики в одном из лучших в мире инструментов для ее создания — ANSYS ICEM CFD. Данный инструмент отлично подходит для создания сетки для CFD-приложений ANSYS — CFX либо FLUENT, однако следует учитывать, что общую логику построения сетки можно переносить и для других приложений, в том числе не ANSYS’овских.
Для начала разберемся с логикой создания сетки, заложенной в ANSYS ICEM CFD. В данном ПО предусмотрена возможность создания двух типов сеток: неструктурированной и структурированной блочной условно гексаэдрической. В рамках данной статьи мы рассматриваем возможность создания именно структурированной блочной гексаэдрической сетки. Методика создания неструктурированной сетки и особенности ее построения будут рассмотрены в последующих статьях. Здесь же лишь упомянем, что в текущей версии ANSYS ICEM CFD существует несколько методов построения объемной и поверхностной неструктурированной сетки. При этом каждый метод имеет несколько алгоритмов построения сетки. Комбинируя различные методы и алгоритмы построения сеток (как поверхностных, так и объемных), пользователь может применять широчайший инструментарий по созданию неструктурированных сеток — от полностью автоматического до ручного создания отдельных элементов. В завершение отметим, что для простой геометрии можно получить неструктурированную сетку, не уступающую по качеству структурированной. Поэтому, говоря о преимуществах структурированной гексаэдрической сетки, мы прежде всего имеем в виду сетку большой размерности, построенную на сложной криволинейной геометрии.
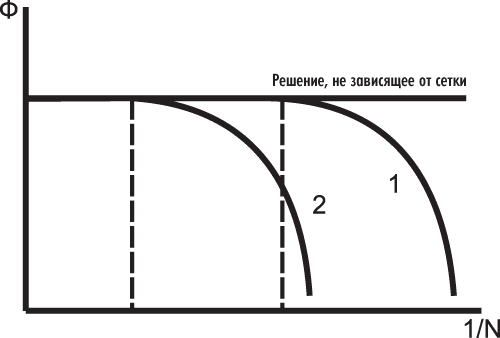
Рис. 1. Получение не зависящего от сетки решения для структурированной и неструктурированной сетки (где Ф — функция, характеризующая зависимость сходимости решения дифференциальных уравнений от количества элементов сетки N): 1 — структурированная гексаэдрическая сетка; 2 — неструктурированная сетка
Следует понимать, что для получения не зависящего от сетки решения (расчетные значения не изменяются при дальнейшем измельчении сетки) количество элементов, а следовательно, и точек интегрирования решаемых уравнений для структурированной гексаэдрической сетки будет меньше, чем для неструктурированной (рис. 1). То есть на гексаэдрической сетке решение, не зависящее от сетки, будет получено за меньшее время счета CPU. Кроме того, пользователи с ограниченными вычислительными возможностями CPU иногда не могут себе позволить построить сетку с большим количеством элементов. В этом случае переход от неструктурированной сетки к структурированной гексаэдрической позволит снизить количество элементов сетки, оставив при этом неизменным характерный размер элементов.
Однако следует понимать, что на построение структурированной сетки понадобится большое количество времени пользователя при значительном снижении машинного. Таким образом, становится очевидном, что структурированную сетку следует строить в случаях, когда лимитирующим фактором для получения решения является продолжительность вычислений, зависящая от возможностей CPU, размера оперативной памяти, объема свободного пространства на жестком диске и т.д. Такая ситуация возникает при моделировании работы однотипных устройств с большим количеством элементов сетки, например оптимизация работы устройства, когда проводится ряд расчетов различных модификаций без принципиального изменения топологии геометрии. В этом случае необходимо единожды затратить время на создание сетки, что затем поможет экономить время при каждом последующем расчете.
Если же необходимо провести разовое моделирование геометрически сложного объекта и при этом нет ограничений по ресурсам CPU, то лучшим решением будет создание неструктурированной сетки.
Теперь, разобравшись, в каких случаях необходимо пользоваться тем или иным методом построения сетки, дадим несколько советов по подготовке сеточной модели для последующего импорта в решатели ANSYS.
Для начала выясним, почему структурированная гексаэдрическая сетка в ANSYS ICEM CFD называется блочной. Дело в том, что для создания структурированной сетки исходную геометрию необходимо описать с помощью блоков — прямоугольников для двумерного и параллелепипедов для трехмерного случая. Проиллюстрируем это на рисунке. В качестве примера возьмем геометрию, представленную в учебных примерах для ANSYS ICEM CFD (рис. 2а), — так, вероятно, читателю будет легче воспроизвести и понять действия, описанные в статье.
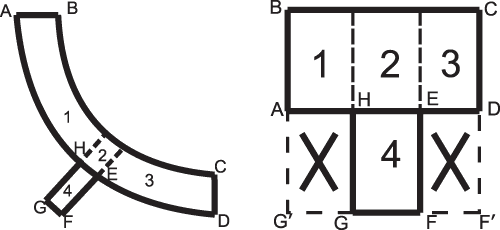
Рис. 2. Исходная геометрия (а) и блочная структура для нее (б)
Для построения гексаэдрической сетки мысленно представляем исходную геометрию (рис. 2а) в виде блоков (рис. 2б). Для создания блочной структуры в ANSYS ICEM CFD существует огромный инструментарий, использование которого значительно облегчает создание блочной структуры. Например, в данном случае (см. рис. 2б) вначале был создан общий блок BCF’G’ (Blocking —> Create Block —> 2D Planar), затем исходный блок был разбит тремя линиями на шесть блоков (Blocking —> Split Block). После этого блоки, отмеченные крестами, были удалены (Blocking —> Delete Block).
При удалении блоков следует быть внимательным к выбору метода удаления блока — полного удаления (Delete permanently) или только перемещения блока в VORFN — семейство блоков, для которых не происходит построение сетки. Дело в том, что вокруг создаваемых блоков всегда существуют дополнительные блоки, необходимые для взаимосвязи между ними. Эти дополнительные блоки можно увидеть, сделав видимым семейство VORFN (Parts —> VORFN). При перемещении ненужных блоков в семейство VORFN изменения структуры блоков не происходит (рис. 3а). При полном удалении блоков (Delete permanently) происходит кардинальное изменение семейства VORFN (рис. 3б), а следовательно, изменение взаимосвязей между блоками. Часть блоков семейства VORFN преобразуется в «О-блоки» (о создании и применении «О-блоков» речь пойдет в следующей статье).
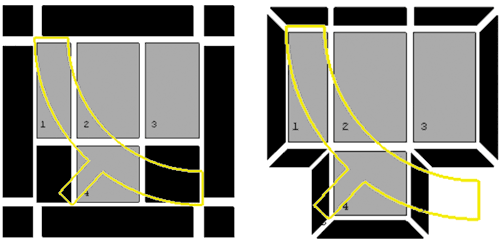
Рис. 3. Вид блочной структуры семейства VORFN (блоки, выделенные черным цветом) в зависимости от метода удаления блоков: a — перемещение в семейство VORFN; б — полное удаление блоков
При создании блочной структуры, особенно для сложной геометрии, не рекомендуется полностью удалять блоки, в которых не нужна сетка. Полное удаление блоков проводится только в случае умышленного изменения структуры и свойств блоков.
После того как мы получили набор блоков, топологически соответствующий исходной геометрии, необходимо провести «ассоциацию» блоков и геометрии (Blocking —> Blocking Associations), то есть определить, каким сторонам геометрии какие ребра блоков соответствуют. В рассматриваемом примере «ассоциация» блоков геометрии выполняется в соответствии с буквенной разметкой геометрии и блоков — ребро АВ «ассоциируется» со стороной AB, BC — с BC и т.д. Таким образом, мы получаем набор блоков, описывающих исходную геометрию (рис. 4). При этом точность описания будет определяться только мастерством пользователя и наличием у него свободного времени.
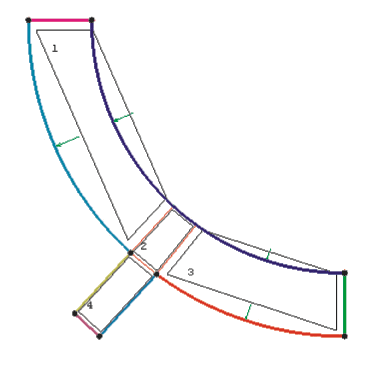
Рис. 4. Набор блоков, описывающих исходную геометрию (стрелками показана ассоциация граней блоков геометрии)
Осталось только задать количество сеточных линий, или размер ячеек (Blocking —> Pre-Mesh Params —> Edge Params), и разбить полученные блоки на сетку. Результатом является предварительная (Pre-Mesh) сетка (рис. 5), которая затем может быть преобразована в сетку с учетом требуемого решателя.
Таким образом, проведя ряд несложных манипуляций, мы получили сетку из практически правильных прямоугольников. Далее можно проводить сгущения в нужных подобластях, создавать пограничный слой и т.д. в зависимости от специфики задачи и потребностей.
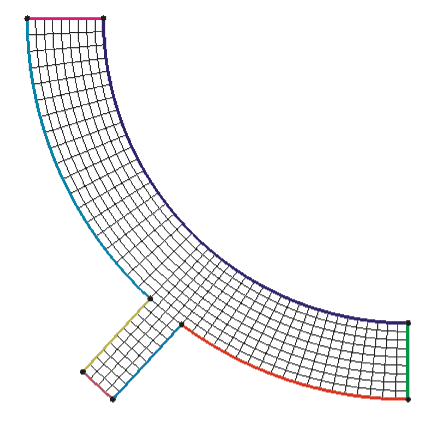
Рис. 5. Полученная условно-гексаэдрическая (прямоугольная для 2D-случая) сетка
Надеюсь, что данная статья заинтересовала читателей и они будут ждать последующие, совершенствуя свои навыки по созданию сетки. Те пользователи, кому не терпится научиться создавать гексаэдрические сетки, всегда могут обратиться в компанию «Делкам-Урал» и пройти специализированный курс по созданию сеток. Кроме того, мы ждем вопросов по e-mail: emm@delcam-ural.ru.


