Построение сложных кривых в Autodesk Inventor

Построение кривых второго порядка

Создание произвольных кривых

Редактирование кривых

Редактирование крылового профиля

Инженерная практика при проектировании изделий различного уровня сложности требует использовать аналитические кривые. К таким кривым можно отнести как кривые второго порядка, так и задаваемые уравнениями. Естественно, конструктор должен иметь возможность не только построить, но и отредактировать кривую в любой момент. Таким образом, применяемая конструктором система САПР должна решать данные задачи. В этой статье вниманию читателей предлагаются алгоритмы, позволяющие строить кривые второго порядка с абсолютной точностью, используя конические сечения, а также аналитические кривые, задаваемые однопараметрическими уравнениями; в случае построения кривой путем задания уравнения применяются сплайны, а точность регулируется количеством точек. Необходимо отметить, что для решения всех указанных задач служат дополнительные модули. Заинтересовавшиеся читатели могут свободно загрузить модули с портала http://www.cadforum.ru/art/. Там же можно ознакомиться со способом подключения модулей.

Построение кривых второго порядка

Из курса аналитической геометрии известно, что существует три вида кривых второго порядка:

• эллипс — кривая, сумма расстояний от каждой точки которой до двух некоторых точек, называемых фокусами эллипса, есть величина постоянная;
• гипербола — кривая, разность расстояний от каждой точки которой до двух некоторых точек, называемых фокусами гиперболы, есть величина постоянная;
• парабола — кривая, расстояния от каждой точки которой до некоторой точки, называемой фокусом параболы, и до некоторой прямой, называемой директрисой параболы, равны. Для построения эллипса в среде плоского эскиза в Autodesk Inventor существует стандартная команда. Что же касается гиперболы и параболы, то такие команды отсутствуют. Однако пользователи легко могут построить любую из этих кривых, воспользовавшись коническими сечениями. Напомним, что парабола является кривой пересечения плоскости и конуса при условии, что плоскость параллельна образующей конуса. А гипербола является кривой пересечения конуса и плоскости при условии, что угол между осью конуса и плоскостью меньше, чем угол между осью и образующей. В частном случае плоскость, результатом пересечения которой с конусом является гипербола, может быть параллельна оси. Частный случай гиперболы — две прямые — получается, если плоскость проходит через вершину конуса.

Итак, сформулируем задачу для построения параболы.

Парабола должна быть построена на плоскости XY детали. Решив задачу построения на плоскости XY, легко распространить полученный результат на любую другую плоскость. Вершина параболы должна лежать в начале координат. Необходимо иметь возможность изменять положение фокуса параболы (и тем самым скорость возрастания функции). Нужно иметь возможность изменять область определения функции (абсциссу последней точки кривой).

Уравнение параболы имеет следующий вид:

y² = 2px ,

где p  — расстояние от фокуса параболы до директрисы.

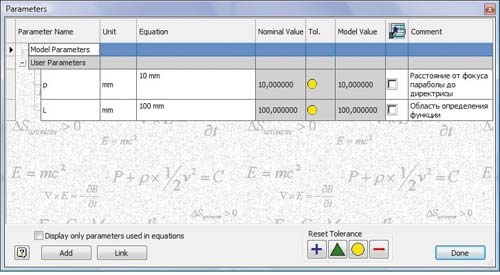
В новом файле детали (*.ipt) открываем таблицу параметров и вводим следующие данные:

Рис. 1

• первый параметр: имя — p; размерность — mm; формула — 10; пояснение — расстояние от фокуса параболы до директрисы;
• второй параметр: имя — L; размерность — mm; формула — 100; пояснение — область определения функции (рис. 1).

Далее опишем последовательность действий по пунктам:

• 1. В созданном на плоскости XZ эскизе проецируем на плоскость эскиза начало координат и чертим горизонтальный отрезок длиной L (тип линии — вспомогательная).
• 2. Чертим наклонный отрезок (тип линии — основная) под углом 30° к первому и налагаем зависимость совмещения между начальной точкой первого отрезка и вторым отрезком. Второй отрезок — образующая будущего конуса.
• 3. Далее в эскизе все линии рисуются как вспомогательные. Чертим третий отрезок, начальная точка которого совпадает с начальной точкой второго отрезка. Из той же точки чертим четвертый, горизонтальный отрезок. Третий отрезок — ось будущего конуса, четвертый — зеркальное отражение его образующей. Между вторым и четвертым отрезком налагаем зависимость симметрии, используя третий отрезок в качестве оси симметрии, а также зависимость равенства.
• 4. Соединяем конечные точки второго и четвертого отрезков новым отрезком и налагаем зависимость совмещения между конечной точкой третьего отрезка и основанием получившегося треугольника.
• 5. Налагаем зависимость совмещения между конечной точкой первого отрезка и основанием треугольника и строим окружность с диаметром, равным длине основания, и центром, совпадающим с конечной точкой третьего отрезка (оси конуса).
• 6. Строим отрезок, начальная точка которого совпадает с конечной точкой первого отрезка, перпендикулярный основанию треугольника. Конечная точка последнего отрезка должна лежать на окружности. Длина отрезка определяется формулой: sqrt(2•p•L) .
• 7. Выходим из эскиза и строим поверхность вращения, используя в качестве образующей второй отрезок, а в качестве оси — третий. Далее вызываем команду Split (Разделить грань) и выбираем в качестве разделяющего элемента плоскость XY , а в качестве разделяемой грани — коническую поверхность. Линия пересечения плоскости и поверхности является параболой.
• 8. Строим эскиз на плоскости XY и проецируем на плоскость эскиза границу участков на конической поверхности. Для оценки кривизны получившейся кривой можно щелкнуть по ней правой клавишей мыши и в контекстном меню выбрать Display Curvature. Настроить эпюру кривизны можно, повторно вызвав контекстное меню и выбрав в нем пункт Setup Curvature Display. Кривизна кривой полностью соответствует кривизне параболы. В целях дополнительной проверки поставим на эскизе точку, задав ее абсциссу как L/4, а ординату как sqrt(2•p•L/4).
  Видно, что точка с такими координатами лежит на кривой.
• 9. Для изменения параболы необходимо войти в таблицу параметров и отредактировать значения p и L. Для примера постройте параболу со значениями p = 16 мм, L = 150 мм.
• 10. Теперь, имея в своем распоряжении параметрическую параболу, можно использовать ее для построения твердотельной геометрии. На рис. 2 показана конструкция, которую можно интерпретировать как вазу, а можно и как сопло ракетного двигателя.

Рис. 2

Сформулируем теперь задачу для построения гиперболы: гипербола должна быть построена на плоскости XY детали. Вершина гиперболы должна находиться на расстоянии от начала координат, равном величине горизонтальной полуоси. Необходимо иметь возможность изменять величины полуосей гиперболы. Требуется возможность изменять область определения функции (разницу между абсциссой последней точки кривой и величиной горизонтальной полуоси).

Уравнение гиперболы имеет следующий вид:

x²/a² – y²/b² = 1 ,

где a  — горизонтальная, b  — вертикальная полуоси гиперболы.

В новом файле детали (*.ipt) открываем таблицу параметров и вводим следующие данные:

• первый параметр: имя — a; размерность — mm; формула — 20; пояснение — горизонтальная полуось гиперболы;
• второй параметр: имя — b; размерность — mm; формула — 15; пояснение — вертикальная полуось гиперболы;
• третий параметр: имя — L; размерность — mm; формула — 100; пояснение — область определения функции.

Далее опишем последовательность действий по пунктам:

• 1. В созданном на плоскости XZ эскизе проецируем на плоскость эскиза начало координат и чертим горизонтальный отрезок длиной L, начальная точка которого находится на расстоянии a от начала координат (тип линии — вспомогательная).
• 2. Строим наклонный отрезок (тип линии — основная) под углом 30° к первому и налагаем зависимость совмещения между спроецированным на плоскость эскиза началом координат и этим отрезком. Налагаем зависимость вертикальности между конечными точками первого и второго отрезков. Построенный отрезок — образующая будущего конуса.
• 3. Далее в эскизе все линии чертятся как вспомогательные. Строим третий отрезок, горизонтальный, начальная точка которого совпадает с начальной точкой второго отрезка. Налагаем зависимость вертикальности между конечными точками второго и третьего отрезков. Третий отрезок — ось будущего конуса.
• 4. Строим окружность с центром в конечной точке оси конуса, при этом конечная точка образующей будет связана с окружностью зависимостью совмещения, то есть радиус окружности равен радиусу основания конуса. Делаем угловой размер справочным. Чертим горизонтальный отрезок (четвертый) с начальной точкой, совпадающей с начальной точкой первого отрезка, и конечной точкой, принадлежащей окружности. Длина отрезка определяется формулой: b•sqrt(((L+a)/a)^2ul-1ul) .
• 5. Строим вертикальный отрезок (пятый), начальная точка которого связана зависимостью совмещения с осью конуса, а конечная точка — зависимостью совмещения с образующей конуса, сам отрезок связан зависимостью совмещения с серединой первого отрезка. Чертим окружность, центр которой совпадает с начальной точкой последнего отрезка, а радиус равен длине этого отрезка. На пересечении окружности и первого отрезка ставим точку. Расстояние между пятым отрезком и точкой определяется формулой: b•sqrt(((L/2ul+a)/a)^2ul-1ul) .
• 6. Строим коническую поверхность вращения и разделяем ее плоскостью XY. Линия пересечения плоскости XY с поверхностью представляет собой гиперболу.
• 7. Дальнейшие действия аналогичны шагам, соответствующим построению параболы. Для дополнительного контроля можно построить асимптоту гиперболы, тангенс угла наклона которой к оси абсцисс равен отношению b/a. Асимптоту также можно получить, спроецировав образующую конуса на плоскость эскиза.

Создание произвольных кривых

Для построения и редактирования кривых необходимо загрузить модуль VBA: http://www.cadforum.ru/_upload/files/CurveBuildnew.rar.

Для построения кривой в среде двумерного эскиза в таблице параметров необходимо задать следующие параметры:

• tParameterMC (размерность любая) — данный параметр является независимым аргументом при определении функции и не может зависеть ни от каких других параметров;
• xParameterMC (размерность — мм) — этот параметр определяет абсциссу текущей точки кривой и должен зависеть от параметра tParameterMC. Кроме того, он может зависеть от любых других параметров;
• yParameterMC (размерность — мм) — данный параметр определяет ординату текущей точки кривой и должен зависеть от параметра tParameterMC. Кроме того, он может зависеть от любых других параметров;
• zParameterMC (размерность — мм) — этот параметр определяет аппликату текущей точки функции и должен зависеть от параметра tParameterMC. Кроме того, он может зависеть от любых других параметров. Параметр zParameterMC применяется при построении трехмерной кривой в среде трехмерного эскиза. При построении плоской кривой в среде двумерного эскиза его наличие необязательно;
• npointsParameterMC (безразмерный параметр) — данный параметр определяет количество точек на кривой;
• deltatParameterMC (размерность совпадает с размерностью tParameterMC) — определяет приращение независимого аргумента tParameter. Необходимо отметить, что циклические зависимости в формулах не допускаются. При построении кривой в среде плоского эскиза из двух параметров (xParameterMC и yParameterMC) хотя бы один из них должен зависеть от tParameterMC. При построении кривой в среде трехмерного эскиза из трех параметров (xParameterMC, yParameterMC и zParameterMC) хотя бы один из них должен зависеть от tParameterMC.

Редактирование кривых

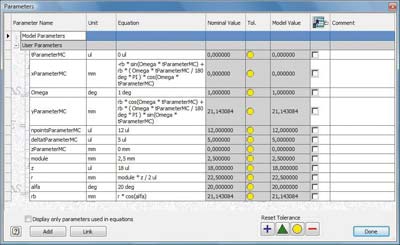
Предположим, что параметры в таблице заданы так, как показано на рис. 3. Представленные уравнения служат для создания эвольвенты, являющейся образующей рабочей поверхности зуба колеса с окружным модулем 2,5 мм и числом зубьев 18.

Рис. 3

Построить эвольвенту можно при помощи программы CurveBuild. Допустим, что при проектировании исходные данные изменились и необходимо построить зуб с модулем 3 мм и числом зубьев 20. В таком случае нужно изменить значения параметров module и z, убедиться, что начальное значение параметра tParameterMC равно нулю, выделить кривую и запустить модуль CurveEdit.

При выборе кривой находиться внутри эскиза необязательно. Необходимо иметь в виду, что если на кривую наложены зависимости, не позволяющие ее перестроить, программа выдаст сообщение об ошибке.

Редактирование крылового профиля

На основании имеющегося опыта можно рассмотреть более сложный пример — построение лопатки с сечением, соответствующим крыловому профилю Чаплыгина — Жуковского.
Как известно из курса аэродинамики, уравнение крылового профиля задается с помощью функции комплексной переменной, осуществляющей конформное отображение окружности радиуса R, построенной на вспомогательной плоскости, на плоскость физическую. Данная функция имеет следующий вид:

где  z = x + i h  — комплексная переменная на вспомогательной плоскости;  z = x +   iy  — комплексная переменная на физической плоскости.
Действительная часть функции z:

Мнимая часть функции z:

Для удобства, а также следуя классической методике построения профиля Чаплыгина — Жуковского необходимо начертить в эскизе, который будет играть роль вспомогательной плоскости, окружность, которую указанная выше функция будет отображать на физическую плоскость, а также окружность, отображение которой является «скелетом» профиля.
В эскизе задан один справочный размер, который используется в таблице параметров. Для корректного построения необходимо, чтобы диаметр окружности, построенной основной линией, был больше диаметра окружности, построенной вспомогательной линией. Соответствующие параметры имеют имена Diam1 (большая окружность) и Diam0 (меньшая окружность). Отображение большей окружности и является крыловым профилем Чаплыгина — Жуковского с нулевым углом на задней кромке.

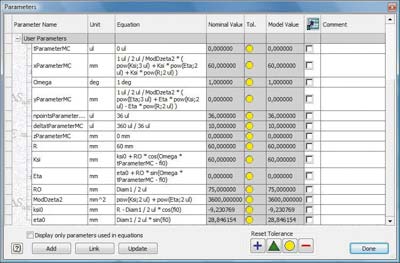
Рис. 4

Таблица с пользовательскими параметрами показана на рис.   4.

Назначение большинства параметров было описано ранее. Прочие параметры:

• R — расстояние от начала координат физической плоскости до задней кромки профиля;
• Ksi — действительная часть комплексной переменной на вспомогательной плоскости;
• Eta — мнимая часть комплексной переменной на вспомогательной плоскости;
• RO — радиус окружности, отображение которой является крыловым профилем;
• ModDzeta2 — квадрат модуля комплексной переменной на вспомогательной плоскости;
• ksi0, eta0 — координаты центра окружности, отображение которой является крыловым профилем, на вспомогательной плоскости.
  Для построения профиля необходимо войти в режим редактирования второго эскиза (Sketch2), убедиться, что начальное значение параметра tParameterMC равно нулю, и запустить модуль CurveBuild.
  Для построения лопатки нужно вызвать команду Coil (Пружина), выбрать результат построения — Поверхность и указать построенный профиль. В качестве оси можно выбрать ось Z. В качестве параметров построения можно выбрать метод, предполагающий задание количества витков и высоты (например, количество витков — 0,1, высота — 400).

Обстоятельство, согласно которому строится именно поверхность, а не твердое тело, нуждается в пояснении. Дело в том, что если построить замкнутый профиль (для этого необходимо изменить значение параметра npointsParameterMC с 36 на 37), то сплайн получится замкнутым, при этом в начальной точке будут выполняться условия непрерывности первой и второй производных. А согласно теории кромка должна быть острой. И хотя с практической точки зрения это не так уж важно, в данном упражнении предлагается сохранять основные свойства крылового профиля.
Для создания твердого тела необходимо вначале замкнуть построенную поверхность. Для этого следует выбрать команду Loft (По сечениям) и указать две кромки, находящиеся в зоне разрыва. В качестве граничных условий нужно задать касательность на обеих кромках (но не совпадение кривизны!). Далее, воспользовавшись командой Boundary Patch (Участок поверхности), можно добавить торцы и сшить полученный набор из четырех поверхностей командой Stich (Сшивка).
Построенный крыловой профиль является излишне изогнутым и толстым. Для его редактирования в первую очередь нужно изменить диаметры окружностей, например, так: Diam1 = 2 ul•R + 10 mm, Diam0 = 2 ul•R + 5 mm. Затем необходимо убедиться, что значение параметра tParameterMC равно нулю. После этого следует выделить соответствующий сплайн, описывающий крыловой профиль, и запустить модуль CurveEdit. (Для того чтобы не входить в режим редактирования эскиза и выбрать именно сплайн, а не кромку поверхности или тела, можно установить приоритет выбора эскизных элементов, предварительно сделав соответствующий эскиз видимым.) После перестроения кривой следует выполнить обновление модели.

www.cadforum.ru

САПР и графика 11`2008