Построение и экстраполяция четырехугольных трехмерных сеток по параметрически заданным моделям
Полигональные сетки являются базовым представлением поверхности тела для большого числа вычислительных задач. Благодаря своей простоте наибольшее распространение получили сетки, состоящие только из треугольных граней. В то же время алгоритмы из области визуализации и физических расчетов на сетках, опубликованные в последние три десятилетия, показывают более высокие результаты при применении сеток с четырехугольными гранями, на характеристики которых наложены определенные ограничения. Необходимо отметить, что для построения таких сеток приходится использовать гораздо более сложные алгоритмы, чем для генерации треугольных сеток. В настоящее время не предложено столь же эффективного и изящного алгоритма, какой, например, можно найти для построения триангуляции Делоне.
Задача построения такой четырехугольной геометрической сетки, соответствующей данной BR rep-модели, — чтобы она удовлетворяла обширному перечню ограничений — встречается во многих приложениях вычислительной геометрии: от численных расчетов до компрессии геометрических данных с потерями и визуализации. Качество построенной сетки зачастую определяет качество всего использующего ее решения.
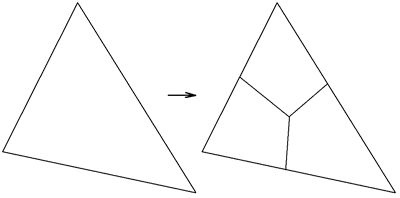
Рис. 1. Тривиальное преобразование триангуляции (разбиение каждого треугольника на три четырехугольника)
Тривиальный подход, состоящий в преобразовании каждой грани триангуляции в три четырехугольника (рис. 1), не представляет интереса, поскольку полностью переносит в генерируемую сетку дефекты триангуляции и добавляет побочные эффекты, не обогащая результат полезными свойствами. Даже для простейших моделей данное преобразование может приводить к получению сеток низкого качества, существенно ухудшая результаты алгоритмов, которые будут применены к модели далее (рис. 2), поскольку привнесут в геометрическую сетку множество граней с углами, сильно отличающимися от прямых, и вершин валентности 3. Необходимо добавить, что данное преобразование может оказаться эффективным, если применить его на одном из заключительных этапов алгоритма к сетке, содержащей минимальное количество треугольников (таким образом можно гарантировать отсутствие треугольников в результирующей сетке).
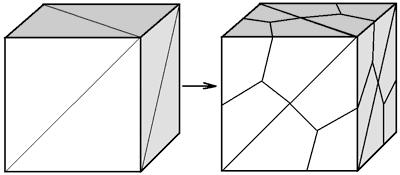
Рис. 2. Пример канонической фигуры, для которой тривиальное преобразование неприемлемо

Рис. 3. Преобразование простой модели, состоящей из четырех фрагментов, в сетку предельного качества
Компания ЛЕДАС активно занялась разработкой решений для построения четырехугольных сеток в 2004 году. Работы велись по трем направлениям:
- разбиение исходной (сложной) модели на фрагменты более простой формы;
- расстановка точек на общих границах фрагментов с целью получить равномерное распределение вершин сетки (для более высокого качества генерируемой сетки) и создать удобные конфигурации для финального алгоритма, заполняющего фрагменты модели четырехугольниками;
- построение геометрической четырехугольной сетки в каждом из построенных фрагментов без добавления новых вершин на границы.
Затем были разработаны алгоритмы постобработки построенной сетки, позволяющие дополнительно повысить качество результатов (прежде всего это обеспечило уменьшение доли треугольников в генерируемой гибридной сетке).
Для тестирования получившегося комплекса алгоритмов применялись сотни промышленных моделей, что позволяло охватить большое количество различных востребованных конфигураций и концентрировать усилия разработчиков на улучшении качества наиболее актуальных свойств. Несколько лет работы над перечисленными алгоритмами позволили сформировать программную систему, генерирующую геометрические сетки высокого качества для произвольных входных моделей. Стало ясно, что дальнейшее улучшение универсального алгоритма является чрезвычайно сложной задачей, поскольку практически все подходы, найденные за время исследования задачи, уже нашли свое применение в программной системе (оставались только решения, на реализацию которых требовалось очень много времени). Поэтому было принято решение разработать группу алгоритмов, генерирующих идеальные сетки (то есть сетки, которые принципиально не могут быть улучшены) для ограниченного набора входных моделей. Кроме того, особенностью этих алгоритмов является возможность строить сетку экстраполированной модели, задавая требуемый допуск (это свойство актуально для различных алгоритмов деформации тел). Такой подход позволяет избавляться от мелких дефектов и несущественных особенностей поверхности.
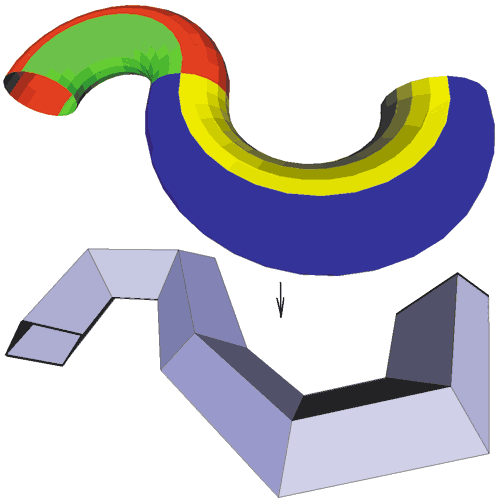
Рис. 4. Преобразование модели, изоморфной цилиндру, состоящей из четырех фрагментов, в сетку предельного качества
После анализа большого количества промышленных моделей, для которых получение идеальных геометрических сеток казалось реалистичной задачей, были сформулированы две идеи:
- среди рассматриваемых моделей распространены два типа, для которых возможна реализация алгоритма, строящего геометрические сетки предельно высокого качества (если требуется, то с заданным параметром экстраполяции). Это позволит для большого количества объективно сложных моделей получить результаты с характеристиками, близкими к идеальным;
- было найдено множество примеров, для которых использование информации о геометрической сущности фрагментов обрабатываемого объекта позволяет в большей степени, чем ранее, улучшить результаты.
Краткое описание алгоритма
В начале процесса происходит последовательное объединение соседних фрагментов BRep-представления модели. При этом необходимо согласовывать ориентацию осей и масштаб UV-представлений исходных фрагментов, чтобы сохранить возможность корректного доступа к точкам поверхности по двум координатам объединения.
На этом этапе происходит формирование новых 3D-поверхностей, которые полностью включают исходные фрагменты, а также экстраполированные поверхности. Когда дальнейшее укрупнение фрагментов невозможно, происходит смещение границ внутреннего представления на величину параметра экстраполяции (рис. 7) и определение типа получившегося множества кусков поверхностей. Анализ многих сотен моделей показал, что два наиболее распространенных типа — это плоскость и цилиндр (в топологическом, а не геометрическом смысле). На рис. 3-5 показаны примеры плоской и цилиндрической моделей, а также цилиндрической модели с отверстием (которое было закрыто благодаря возможности экстраполировать за пределы границы объекта). На рис. 6 представлена модель, объединение фрагментов которой было отнесено к типу топологически плоских, для которой была восстановлена большая часть вырезанной области (отметим, что только для далеких от границы модели вершин заметен небольшой дефект экстраполяции). На примере данной модели можно убедиться, что алгоритм успешно объединяет области, у которых направления изолиний на границах существенно различаются.
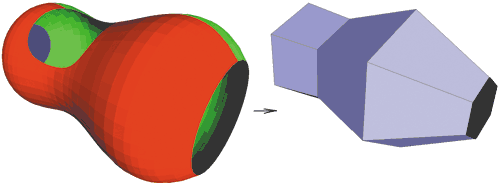
Рис. 5. Преобразование модели, изоморфной цилиндру с отверстием, в сетку предельного качества
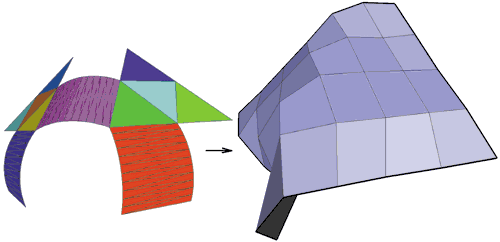
Рис. 6. Преобразование плоской в топологическом смысле модели в сетку предельного качества
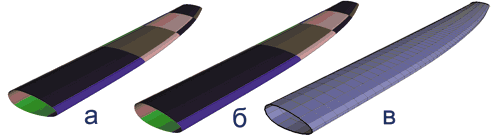
Рис. 7. Три шага преобразования модели «крыло»: а — объединение фрагментов, пока это возможно (крыло изоморфно цилиндру); б — расширение границ внутреннего представления на свободных границах (экстраполяция); в — построение четырехугольной геометрической сетки предельного качества
При оценке результатов работы алгоритмов используется большое количество естественных индикаторов: отношение длин смежных ребер, отклонение углов граней от среднего угла, отклонение нормалей смежных граней, расстояние от точек построенной сетки до исходной модели, отношение количества треугольников к количеству четырехугольников в гибридной геометрической сетке и т.д. Обязательными требованиями к результирующей геометрической сетке для дальнейшего использования в расчетных задачах являются:
- многообразность для замкнутых поверхностей, представляющих границу тела;
- ориентированность (согласованность ориентации для каждой пары смежных граней);
- выпуклость четырехугольных граней.
В данной работе удалось добиться построения четырехугольных сеток с перечисленными ограничениями. К достижениям можно отнести следующее:
- результатом работы алгоритмов всегда является четырехугольная сетка (в предшествующих работах удавалось только заметно понизить долю треугольников в гибридной сетке, но не всегда получалось полностью от них избавиться);
- рост показателей качества из-за применения новых подходов при построении сеток для фрагментов канонических фигур;
- возможность экстраполировать исходную модель, что расширило применимость алгоритмов.
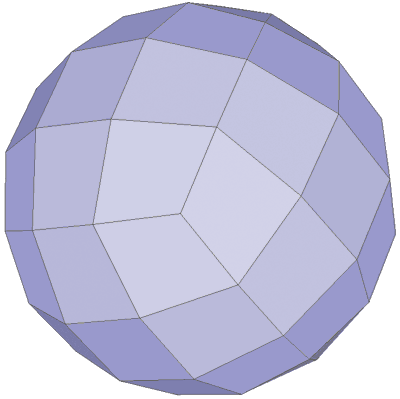
Рис. 8. Четырехугольная сетка для сферической модели (сетка содержит вершины валентности 3, но в данном случае это обусловлено типом модели)
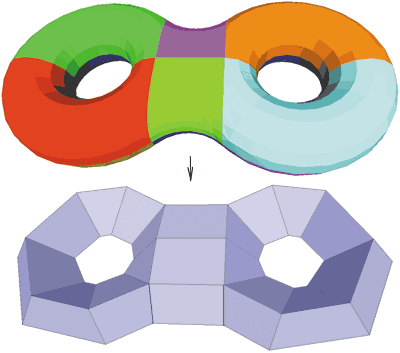
Рис. 9. Преобразование модели, изоморфной сфере с двумя ручками, состоящей из 12 фрагментов, в сетку предельного качества
Построенная в результате работы алгоритма геометрическая сетка удовлетворяет заявленным требованиям при условии, что исходная BRep-модель была корректна.
Следующим шагом на пути к получению качественных четырехугольных сеток является такое расширение полученной группы алгоритмов, чтобы они могли строить сетки предельного качества не только для плоских моделей и моделей, изоморфных цилиндру, но и для объектов других типов. В настоящее время предприняты усилия для получения качественных результатов для моделей, изоморфных шару, тору (шару с ручкой), тору с ручкой и т.д. (рис. 8 и 9). Для этих объектов, естественно, сохраняются все ранее достигнутые преимущества данной группы алгоритмов: возможна экстраполяция (а значит, есть возможность удалять несущественные отверстия), сетка состоит только из четырехугольников (что избавляет от необходимости применять различные алгоритмы для уменьшения доли и удаления треугольников).
Подводя итоги, можно сказать, что компания ЛЕДАС разработала наукоемкое решение, которое может найти применение при решении широкого круга задач САПР и вычислительной геометрии. Более подробную информацию можно получить по адресу: info@ledas.com.


