Статистическое моделирование спектров упругоотраженных электронов

Александр Батраков, Александр Лубенченко

Введение

Моделирование рассеяния электронов

Результаты моделирования и их анализ

Наиболее перспективным методом исследования поверхности конструкционных материалов является метод спектроскопии отраженных электронов (СОЭ). Метод СОЭ может быть реализован на стандартном аналитическом оборудовании (например, Оже-спектрометре), которое отличается малыми габаритами. Преимущество данного метода анализа в том, что он не оказывает разрушающего действия. Энергетические спектры электронов, отраженных в единичный элемент телесного угла, содержат обширную информацию о послойном и компонентном составе поверхности исследуемой мишени. Трудности теоретической интерпретации спектров затрудняют применение метода СОЭ. В работе используется метод имитационного моделирования при интерпретации данных СОЭ.

Введение

Задача исследования водородосодержащих материалов возникает во многих областях науки и техники. Например, первая стенка термоядерной установки подвержена сильному воздействию ионов изотопов водорода. Одним из материалов первой стенки является углерод. При анализе поверхности первой стенки методом СОЭ появляется возможность детектирования изотопов водорода [1], что проблематично в других методах анализа [2]. В данной работе решается задача интерпретации данных, полученных методом СОЭ.

Моделирование рассеяния электронов

Разработана программа моделирования траектории частиц в неоднородных средах, реализованная в математическом пакете Matlab [3]. Траектория частицы в среде моделируется классическим прямым методом Монте­Карло [4]. Расчет траектории частицы заключается в вычислении длины свободного пробега (расстояния между узловыми точками) и розыгрыша типа столкновения (упругого или неупругого) в узловой точке, после чего частица изменяет свое состояние: движется в новом направлении с новой энергией до тех пор, пока не произойдет новое столкновение, и т.д. Тип столкновения определяется величинами сечения упругого рассеяния   и сечения неупругого рассеяния . Для вычисления длины свободного пробега необходимо значение полного сечения:

. (1)

В работе было использовано дифференциальное сечение упругого рассеяния [6] в диапазоне начальных энергий, используемых в работе, которое совпадает с формулой Резерфорда. Поэтому розыгрыш угла рассеяния в программе реализуется по формуле:

, (2)

где  — параметр экранирования,  — угол рассеяния, R — случайное число, что значительно уменьшает время расчета траектории. Упругие потери энергии электронов, отраженных от ядер, вычисляются на основании классических законов сохранения энергии и импульса и определяются соотношением масс электрона (m) и массы ядра мишени (M) [1]:

, (3)

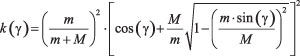, (4)

где  — кинематический фактор, E0 — энергия электрона. Разработанная программа позволяет моделировать рассеяние частиц в среде, неоднородной как по составу, так и по пространству. Длина свободного пробега в неоднородной среде рассчитывается по методу постоянного сечения [5]. Согласно этому методу выберем произвольную постоянную   и обозначим через   разность . Условимся считать, что при столкновении, кроме рассеяния и поглощения, возможно фиктивное столкновение, при котором ни энергия, ни направление не меняются. Сечение (коэффициент) фиктивного столкновения будем считать равным . Вероятность соответствующих типов рассеяний равна ,  , а вероятность фиктивного столкновения — . Длина свободного пробега вычисляется по формуле:  , а тип столкновения разыгрывается с учетом всех трех возможностей.

Поскольку при увеличении   количество фиктивных столкновений возрастает, то обычно стараются выбрать минимально возможное значение, то есть . При расчете угловых распределений применяется равномерная сетка по телесному углу, что позволяет уменьшить дисперсию по сравнению с использованием равномерной сетки по полярному углу.

Для обнаружения водорода наиболее важен упругий канал рассеяния, если электрон попадает в неупругий канал — он считается поглощенным.

Сечение неупругого рассеяния и концентрация ядер взяты из литературы [6].

Сечение упругого рассеяния и параметр экранирования получены с помощью программы NIST [7].

Результаты моделирования и их анализ

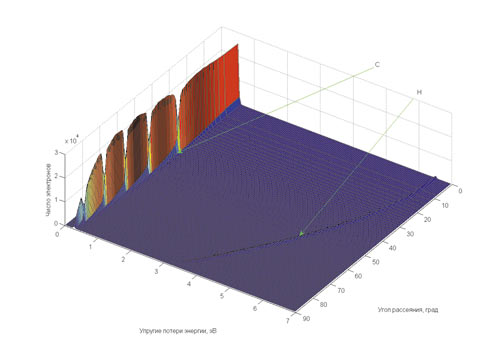
Промоделировано рассеяние электронов с начальной энергией 3000 эВ на полубесконечном слое СН2 при разных углах падения электронного пучка (0, 15, 30, 45, 60, 75° от нормали к поверхности). На рис. 1 представлено энергетическое и угловое распределение отраженных электронов при нормальном падении пучка электронов от полубесконечного слоя СН2. По результатам моделирования можно сделать следующий вывод: увеличение угла падения приводит к незначительному росту величины упругого пика на водороде, при этом пик смещается в область малых потерь энергии, что затрудняет его детектирование. Таким образом, углы падения и детектирования, близкие к нормали, значительно упрощают детектирование водорода. Для этих геометрий были проведены следующие расчеты.

Рис. 1. Энергетическое и угловое распределение отраженных электронов

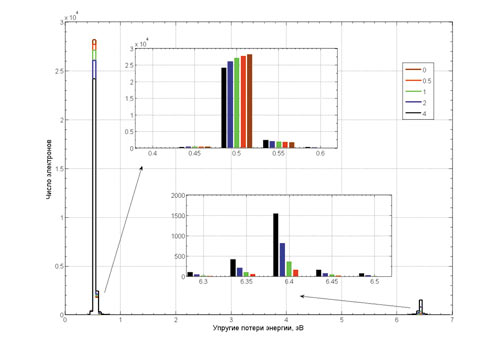
На рис. 2 представлено влияние стехиомет­рического коэффициента X (CH_X) при рассеянии электронов (общее число отраженных электронов — 3 млн, начальная энергия — 3000 эВ), нормально падающих на полубесконечный слой CH_X, угол детектирования — 15° от нормали, в легенде рисунка указана величина стехиомет­рического коэффициента. При анализе рис. 2 видно, что упругий углеродный пик соответствует потерям энергии 0,4­0,6 эВ, а упругий водородный пик — 6,3­6,5 эВ.

Рис. 2. Энергетические спектры отраженных электронов при различных значениях стехиометрического коэффициента

В работе было промоделировано рассеяние электронов с начальной энергией 3000 эВ, нормально падающих на слой углеводорода СН₂, в котором концентрация водорода:

1) линейно падает до нуля на глубине 8 нм;

2) имеет вид «ступеньки» глубиной 4 нм;

3) постоянна.

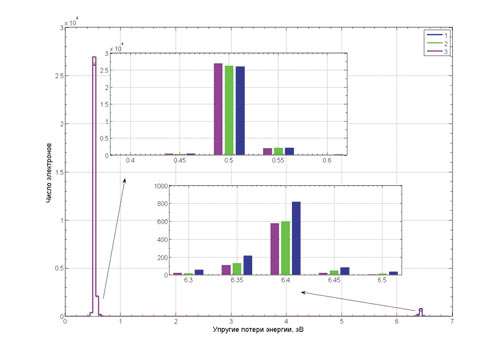
На рис. 3 нумерация в легенде совпадает с приведенной выше в спис­ке, угол детектирования — 15° от нормали, общее число отраженных электронов — 3 млн.

Статистическая обработка результатов моделирования проводилась по 3 млн вылетевших электронов, при этом статистическая погрешность приблизительно 0,1% — это гораздо меньше погрешности исходных величин (сечений, концентрации и т.д.).

Рис. 3. Энергетические спектры отраженных электронов при различной концентрации водорода

Проведенное моделирование показало принципиальную возможность детектирования водорода в твердом теле методом СОЭ. По результатам моделирования были сделаны выводы о наилучшей геометрии эксперимента и требованиях, предъявляемых к разрешающей способности энергоанализатора. Углы падения и детектирования, близкие к нормали, являются наиболее выгодными для детектирования водорода. При разрешающей способности энергоанализатора 0,2 эВ возможно уверенное обнаружение водорода в твердом теле, концентрация которого составляет 0,1 г/см³. Если разрешающая способность 0,05 эВ, то это позволяет проводить послойный анализ распределения водорода по глубине.

Список литературы

Афанасьев В.П. Определение послойных профилей изотопов водорода и гелия методами электронной спектроскопии// Поверхность. 2005. № 3. С. 19­23.

Фелдман Л., Майер Д. Основы анализа поверхности и тонких пленок. М.: Мир, 1989.

Батраков А.А., Лубенченко А.В. Сборник аннотаций 4­й Курчатовской молодежной научной школы. 2006. С. 87.

Михайлов Г.А. Некоторые вопросы теории методов Монте­Карло. Новосибирск: М.: Наука, 1974.

Соболь И.М. Численные методы Монте­Карло. М.: Наука, 1973.

Tan Z. Electron stopping power and mean free part in organic compounds over the energy range of 20­10000 eV. Beam Interaction with Materials & Atoms. 2004. Р. 27­43.

Jablonski A., Salvat F., Powell C.J. NIST Electron Elastic­Scattering Cross­Sections Database — Version 3.0/ National Institute of Standards and Technology. Gaithersburg: MD, 2002.

Александр Батраков

Аспирант кафедры общей физики и ядерного синтеза МЭИ (ТУ).

Александр Лубенченко

Докт. техн. наук, доцент кафедры общей физики и ядерного синтеза МЭИ (ТУ).

САПР и графика 11`2009