Построение трехмерной сетки детали для расчета распределения гальванического покрытия по ее поверхности
В разрабатываемой в Тамбовском государственном техническом университете САПР гальванических процессов для расчета распределения гальванического покрытия по поверхности детали в электрохимической ванне необходимо рассчитать электрическое поле в ее объеме. При этом численным методом релаксации с прогонкой по строке решается уравнение Лапласа с нелинейными краевыми условиями третьего рода. Данный метод на первом этапе предусматривает разбиение объема электролитической ванны трехмерной сеткой. Для этого необходимо задать геометрические характеристики объекта: размеры ванны, расположение, форму и размеры анода и катода (покрываемой детали). Расположение анода и геометрические размеры ванны, как правило, известны из технологических особенностей оборудования. Наибольшую сложность представляет геометрическое описание поступающих на обработку деталейкатодов. Поскольку на предприятиях информация о большинстве деталей представлена в виде машиностроительных чертежей на бумажных носителях, первым этапом работы алгоритма является сканирование чертежа и перевода полученной информации из растровой в векторную форму.
Задача данного исследования ставится следующим образом. Пусть известно векторное описание трех проекций деталикатода. Для решения уравнения Лапласа необходимо знать координаты только тех точек поверхности детали, которые обращены к аноду. То есть трехмерные координаты узлов сетки, которой с определенным шагом разбита обращенная к аноду сторона детали.
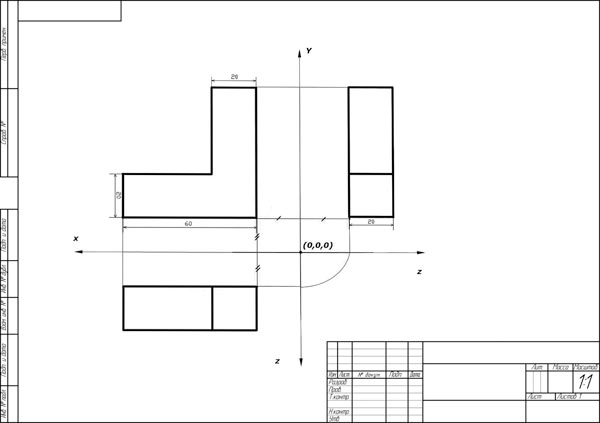
Рис. 1. Три проекции детали на чертеже
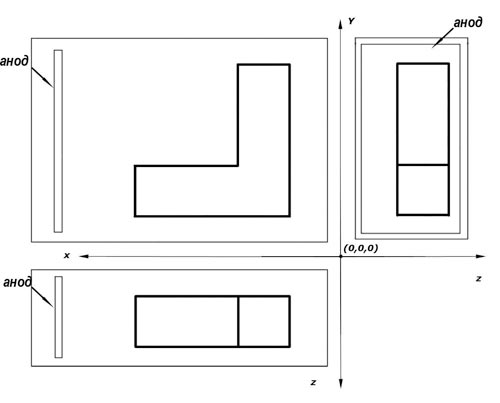
Рис. 2. Положение ванны, анода и детали на чертеже в трех видах
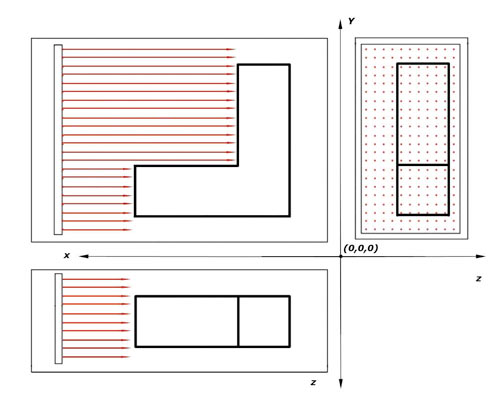
Рис. 3. Сетка нормалей на чертеже в трех видах
Для привязки к ортогональной системе координат необходимо найти начало координат на основе информации о трех проекциях детали (рис. 1).
Алгоритм состоит из следующих этапов:
1. Зная положение анода в ванне, восстанавливаем нормали к его поверхности в узлах сетки, используемой для расчета гальванического покрытия.
2. Проецируем объем ванны с анодом на векторный чертеж с учетом расположения детали в ней (рис. 2).
3. На основе информации о нормалях, полученной в п. 1, находим точки их пересечения с поверхностью детали путем проецирования нормалей на двумерный векторный чертеж (рис. 3).
4. Точки, расположенные ближе к аноду, являются точками поверхности, обращенной к аноду. По их проекциям на оси координат получаем трехмерные координаты точек в объеме ванны (на рис. 4 показана точка поверхности и ее координаты).
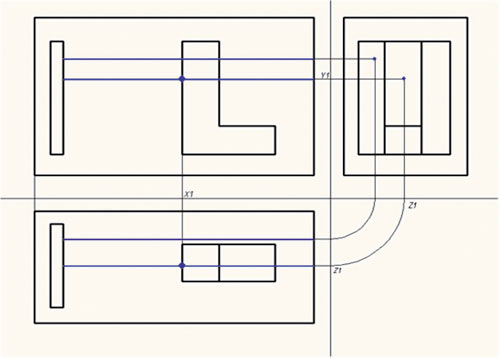
Рис. 4. Точка пересечения нормали с поверхностью детали
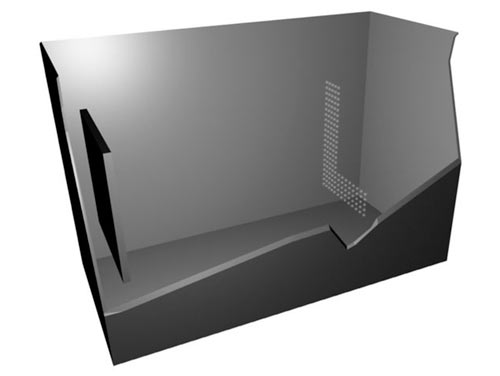
Рис. 5. Трехмерная сетка поверхности катода
Данный алгоритм обладает рядом преимуществ:
- на выходе мы получаем данные, которые можно сразу передавать в алгоритм расчета электрического поля;
- сокращено количество вычислений и соответственно объем памяти, требуемый для вычисления и хранения модели детали по сравнению с расчетом геометрического места всех точек поверхности детали, для которых рассчитывается электрическое поле;
- упрощается работа с катодом достаточно сложной формы и наличием отверстий.
Рассмотрим отдельно пункты 3 и 4 алгоритма, так как они являются основными. Каждая из задач пункта 3 о нахождении точек пересечения проекций нормалей с проекцией катода и задача пункта 4 о нахождении координат точек, ближайших к поверхности анода, могут быть решены по следующему алгоритму:
1. Для выбранной нормали N(i),
i = 1,2, … nN (nN — количество нормалей), заданной в виде системы параметрических уравнений:
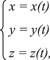
будем искать пересечение со всеми отрезками векторизованного изображения: M1(j), M2(k), M3(l), j = 1,2 ... nM1, k = 1,2 ... nM2, l = 1,2, ... nM3.
Для точек М1:
![]()
Для точек М2:
![]()
Для точек М3:
![]()
Для нахождения координат точек необходимо решить системы линейных уравнений для каждого из отрезков и каждой из трех проекций.
2. Полученные массивы точек исследуем на совпадение координат точек пересечения (с заданной точностью) для разных проекций (соответствие координат показано на рис. 4).
3. На основе совпадения координат получаем массив точек пересечения луча с объектом, находим в нем точку, расположенную наиболее близко к поверхности анода.
Данный алгоритм требует большого количества вычислений, особенно при мелком шаге сетки. Как следствие, алгоритм работает медленно. Для сокращения времени его работы предлагается рассматривать каждую задачу пп. 3 и 4 как отдельную, не связанную с другими, и решать их параллельно на многопроцессорных (многоядерных) вычислительных системах. Действительно, фактически мы имеем не связанные друг с другом задачи. Даже более того — каждая из задач пп. 3 и 4 может быть разбита на ряд не связанных друг с другом. Рассмотрим варианты разбиения задачи для различных вычислительных систем, различающихся количеством вычислителей:
1. Два вычислителя (два процессора или два ядра в одном процессоре) — задачу следует разбить на две подзадачи. Один вычислитель считает одну половину точек поверхности, а второй — другую (средний выигрыш от такого разбиения — порядка 3040%).
2. Три вычислителя (три процессора или трехъядерный процессор) — задача разбивается на три части аналогично п. 1 (средний выигрыш от такого разбиения — порядка 5060%).
3. Четыре вычислителя (аналогично трем) — средний выигрыш от такого разбиения — порядка 6070%.
4. Десять вычислителей — средний выигрыш от такого разбиения — порядка 8085%.
5. Сто и более вычислителей (SIMDпроцессор или группа SIMD процессоров — почти все современные мощнейшие суперкомпьютеры и видеокарты нового поколения) — для данного варианта лучше всего использовать не только разбиение на каждый вычислитель по элементарной задаче, но и разбиение каждого определения пересечения точек для пункта а (задачи пп. 3 и 4), а также отдельно для каждого получения трехмерной точки в пункте б (задачи пп. 3 и 4). Это является наиболее выгодным разбиением, так как данные системы, как правило, имеют собственный аппаратно реализованный менеджер задач, который равномерно распределяет задачи по вычислителям в зависимости от их загрузки, что позволяет достичь очень высокой производительности расчета параллельно реализованных задач (более 90%).
Данный алгоритм обладает рядом преимуществ, что дает возможность не применять дополнительные алгоритмы, которые будут строить сетку поверхности модели. Также алгоритм имеет большой потенциал для построения его распараллелизованной версии, что сокращает время, затрачиваемое на его расчет. Мы считаем его перспективным вариантом для систем, рассчитывающих процесс нанесения гальванического покрытия.
Пример полученной трехмерной сетки для детали, показанной на рис. 1, приведен на рис. 5.


