Автоматизация построения математической модели поверхности летательных аппаратов

Прокопий Николаев, Александр Разов

Введение

Структура хранения данных о геометрии ЛА

Алгоритм построения математической модели

Результаты

Литература

Введение

В настоящее время математические модели поверхности нашли широкое применение на разных этапах проектирования летательных аппаратов (ЛА). Например, при расчете аэродинамических характеристик летательного аппарата и его элементов с помощью численных методов расчета динамики жидкости и газа, основанных на конечно­разностном решении осредненных по Рейнольдсу уравнений Навье-Стокса, первоначально необходимо подготовить математическую модель поверхности, что является непростой задачей, требующей значительных затрат времени. Если для этой цели использовать существующие CAD-системы широкого применения, то потребуется большая доля ручного труда для внесения данных с чертежа или таблиц.

Для построения геометрической модели пользователь вначале должен представить исходные данные (обычно это наборы координат точек) в формате, который воспринимается системой проектирования, или вручную ввести эти координаты. Далее строятся интерполяционные кривые для каждого сечения, а по ним — поверхности. Внесение даже небольших изменений в математическую модель ЛА вызывает необходимость перестройки вручную большей ее части. В то же время многие операции являются типовыми и могут быть выполнены в автоматизированном режиме.

В некоторых программах аэродинамического расчета геометрические данные ЛА представляются в виде текстовых таблиц с набором координат точек, описывающих форму в плане и профили сечений крыла, сечения фюзеляжа и других агрегатов ЛА. Такой способ задания поверхности ЛА называется каркасной моделью и является очень удобным для пользователей этих программ, особенно при необходимости рассмотрения большего количества вариантов компоновки. В работе создан алгоритм и программа, которые позволяют автоматизировать процесс построения поверхности трехмерной модели, используя упомянутую выше текс-товую таблицу.

Первым этапом создания такой программы стала разработка структуры хранения данных, описывающих геометрические параметры компоновки ЛА. За основу этой структуры был взят геометрический блок исходных данных аэропрочностной системы «АРГОН» [1; 2]. На втором этапе был разработан алгоритм, который по данным описания геометрии ЛА создает файл формата IGES [3], воспринимаемый большинством CAD-систем и программами построения расчетных сеток.

Структура хранения данных о геометрии ЛА

Формат файла с описанием компоновки, который используется в качестве геометрического блока исходных данных для системы «АРГОН», предполагает, что вся компоновка ЛА разбивается на агрегаты (фюзеляж, крыло, оперение, подвески и т.д.), которые могут быть двух типов:

• слабоизогнутые несущие поверхности (тип «крыло»);
• объемные тела (тип «фюзеляж»).

Объемные тела задаются набором сечений, перпендикулярных оси Х (ось Х направлена вдоль продольной оси ЛА) (рис. 1), а несущие поверхности задаются набором сечений, параллельных оси Х. Кроме того, для агрегата типа «крыло» могут быть заданы наборы профилей и углы крутки сечений (рис. 2). На агрегатах типа «крыло» могут находиться управляющие поверхности (де-флекторы).

Рис. 1. Каркасная модель фюзеляжа

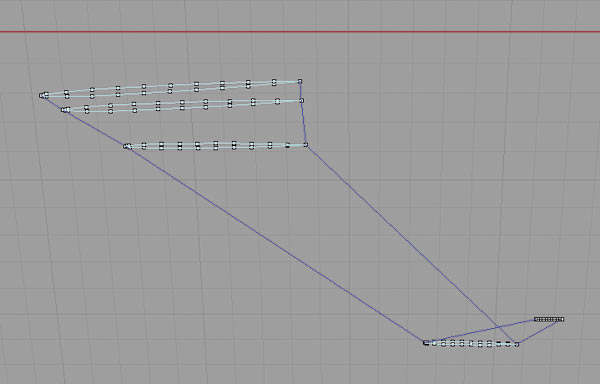
Рис. 2. Каркасная модель крыла

При разработке собственной системы хранения данных необходимо было, во-первых, обеспечить ее удобное заполнение и полную совместимость с упомянутым выше форматом данных, а во-вторых, предусмотреть ее гибкость и возможность увеличения числа параметров.

Внутренняя база данных программы представляется в следующем виде. Компоновка ЛА хранится в базе данных в виде двух списков. Первый содержит информацию об агрегатах ЛА, которые, как и в системе «АРГОН», могут быть двух типов: «крыло» — несущие поверхности и «фюзеляж» — объемные тела.

Второй список содержит информацию обо всех профилях, используемых в агрегатах типа «крыло». В программе «АРГОН» информация о профилях представляется в отдельном файле в виде набора координат точек, описывающих контур профиля на его нижней и верхней поверхности. Однако для задач проектирования и оптимизации формы профиля удобно применять его аналитическое представление [4]. Поэтому список профилей может содержать как профили, заданные набором координат точек каркаса профиля, так и профили, заданные аналитически.

Структура базы данных, описывающая агрегаты типа «крыло» (крыло, горизонтальное и вертикальное оперение, пилоны двигателей, гребни и т.д.), содержит следующую информацию:

• форма в плане, заданная в виде набора поперечных сечений, каждое из которых содержит координаты передней кромки сечения и длину хорды в данном сечении;
• крутка, заданная в виде набора углов крутки в различных сечениях по размаху крыла и положени. центра вращения на хорде;
• профилировка, заданная в виде набора профилей в различных сечениях по размаху с указанием масштаба толщины;
• органы управления, заданные в виде набора отдельных трапециевидных элементов, для которых установлены положения левого и правого края по размаху, положение переднего края по хорде, хорда самого элемента и угол отклонения данного элемента.

Структура базы данных, описывающая агрегаты типа «фюзеляж» (фюзеляж, гондолы двигателей, баки и т.д.), содержит следующую информацию: набор сечений, перпендикулярных продольной оси, с указанием положения сечения на оси и формы сечения, которая может быть задана двумя способами:

• круговым сечением;
• сечением произвольной формы в виде набора координат точек этого сечения.

В соответствии с форматом файла исходных данных структура базы данных каждого агрегата содержит сведения о местной системе координат, если таковая использовалась для описания данного агрегата. В исходном формате местная система координат определяется положением точки начала отсчета и поворотом относительно оси, параллельной оси X глобальной системы координат. Однако во внутренней структуре хранения данных местная система координат может быть задана и общим образом: положение точки начала отсчета, направление местной оси X и ориентацией местной оси Y.

Как только внутренний формат хранения данных о компоновке ЛА становится расширенным по сравнению с форматом файла исходных данных, возникает необходимость сохранения данных в файл в формате, удобном для чтения. Для этих целей был выбран формат XML [5], который удобно читать как программным способом, так и визуально. XML (eXtensible Markup Language) — расширяемый язык разметки, фактически представляющий собой свод общих синтаксических правил. XML — текстовый формат, предназначенный для хранения структурированных данных (взамен существующих файлов баз данных) и обмена информацией между программами. Таким образом, имеющаяся структура данных о геометрии ЛА может быть легко и наглядно представлена и сохранена в формате XML (рис. 3).

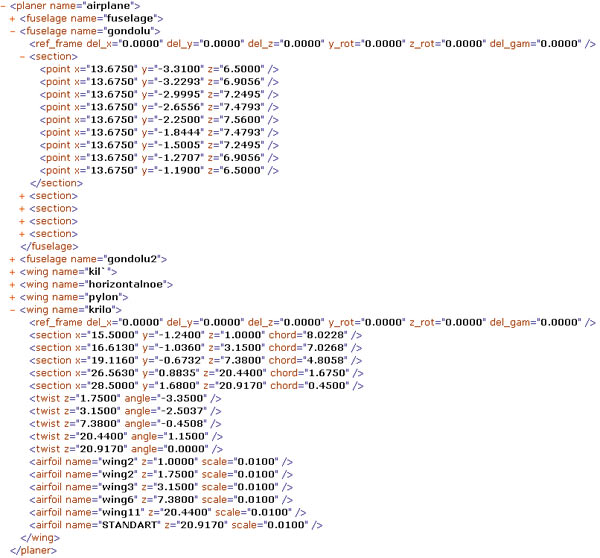
Рис. 3. Фрагмент XML-файла с описанием компоновки ЛА

Алгоритм построения математической модели

Был разработан алгоритм и написана компьютерная программа, которая позволяет, используя исходные данные в виде текстовых таблиц программы «АРГОН» с описанием геометрических параметров компоновки ЛА, получить файл формата IGES, содержащий математическую модель поверхности ЛА. Данная программа применяет внутренний формат хранения информации о геометрии ЛА, описанный выше. В программе можно выделить следующие основные модули:

1. модуль импорта исходных данных во внутренний формат программы;

2. модуль построения поверхностей по данным описания геометрии ЛА;

3. модуль записи поверхностей в IGES-файл.

Основной модуль программы — второй. Первый и третий модули являются соответственно интерфейсами чтения и записи входных и выходных данных и могут быть заменены для работы с альтернативными форматами. Рассмотрим алгоритм работы второго модуля подробнее.

Для описания геометрии ЛА были выбраны NURBS-поверхности как наиболее удобное и универсальное средство описания геометрии [6]. NURBS-поверхности задаются с помощью прямоугольной сетки контрольных точек и двух узловых векторов для поперечного и продольного направления соответственно. Для построения NURBS-поверхностей (то есть определения контрольных точек и узловых векторов) по набору точек, лежащих на этой поверхности, использовался метод локальной бикубической интерполяции с условием непрерывности первых производных по обоим направлениям во всех точках [7]. Для применения этого метода необходимо, чтобы набор точек поверхности представлял собой двумерную сетку точек с размерностью больше четырех в каждом направлении.

Однако практика применения данного подхода для реальной компоновки показала, что использование кубической интерполяции в продольном направлении является, во-первых, не всегда возможным в силу отсутствия четырех сечений, а во-вторых, в ряде случаев дает нежелательные искажения поверхности. Поэтому, кроме бикубической интерполяции, был запрограммирован алгоритм линейно­кубической интерполяции. При использовании этого алгоритма непрерывными остаются первые производные только в поперечном направлении. Выбор способа интерполяции остается за пользователем и не может производиться в автоматическом режиме.

Перейдем к подготовке данных для построения поверхностей. Как уже было описано, для построения NURBS-поверхности методом локальной интерполяции необходимо иметь сетку точек, лежащих на данной поверхности. Таким образом, необходимо решить задачу перевода данных о геометрии агрегатов ЛА в двумерные массивы координат точек поверхностей.

В случае агрегата типа «фюзеляж» задача имеет относительно простое решение. Этот агрегат описывается набором поперечных сечений. Если все сечения заданы одинаковым числом точек, то никаких дополнительных операций не требуется. Если сечения представлены разным количеством точек, то необходимо произвести перерасчет точек. Для этого через сечения проводятся NURBS-кривые методом кубической интерполяции и с их помощью рассчитываются новые точки, определяющие данные сечения, при этом количество новых точек равно максимальному количеству точек в исходных сечениях.

Как уже говорилось, каждый агрегат также характеризуется еще и местной системой координат. Поэтому для получения окончательного массива точек поверхности ко всем полученным точкам необходимо применить операцию смещения и поворота системы координат.

Перейдем к рассмотрению агрегата типа «крыло». Здесь решение задачи по построению сетки точек искомой поверхности несколько усложняется, так как информация о геометрии «крыла» разделена на отдельные части: форма в плане, крутка, профилировка. «Крыло» разбивается поперечными сечениями на отдельные секции, имеющие постоянную стреловидность передней и задней кромок. Сетка точек на поверхности агрегата формируется отдельно для верхней и нижней поверхностей каждой секции.

Прежде всего, исходя из данных о форме в плане, методом линейной интерполяции определяются положение передней кромки и величина хорды во всех точках по размаху «крыла». Также по данным крутки в заданных сечениях линейной интерполяцией определяется крутка в произвольном сечении по размаху. Затем определяются профили, относящиеся к рассматриваемой секции. Координаты точек профиля масштабируются в соответствии с заданными величинами хорды и относительной толщины и совмещаются с положением передней кромки. Далее к координатам точек профиля применяется поворот в соответствии с заданной круткой. В завершение учитываются смещение и поворот локальной системы координат.

Вся эта процедура описана для случая, когда профили заданы одинаковым числом точек контура. Если же профили имеют разное число точек или есть профили, заданные аналитически, то все они пересчитываются на максимально встречающееся число точек аналогично тому, как это делалось для сечений фюзеляжа.

На основе полученных сеток точек поверхностей агрегатов ЛА c помощью бикубической и линейно­кубической локальной интерполяции строятся NURBS-поверхности, которые затем передаются в модуль записи IGES-файла. В этом модуле используется отдельно разработанная библиотека функций для работы с данным форматом.

Результаты

Полученная математическая модель поверхности ЛА в формате IGES может быть использована для построения расчетных сеток с помощью специального программного обеспечения и далее для аэродинамического расчета. На рис. 4 приведена математическая модель пассажирского самолета с построенной поверхностной неструктурированной расчетной сеткой.

Рис. 4. Математическая модель пассажирского самолета с поверхностной расчетной сеткой

Литература

1. Евсеев Д.Д., Ишмуратов Ф.З., Липин Е.К., Чедрик В.В. и др. Комплекс программ аэродинамического проектирования «АРГОН»//Ученые записки ЦАГИ. Т. XXII. 1991. № 5. С. 88-101.

2. Ishmuratov F.Z., Chedrik V.V. ARGON Code: Structural Aeroelastic Analisis and Optimization//International Forum on Aeroelasticity and Structural Dynamics, Amsterdam, 2003.

3. The Initial Graphics Exchange Specifcation (IGES) Version 6.0, 1998.

4. Кутищев Г.П., Теперин Л.Л. Применение аналитического представления контура профиля для решения обратной задачи аэродинамики//Труды ЦАГИ. Вып. 2655. Численные методы аэродинамического проектирования. 2003.

5. Extensible Marup Language (XML) 1.0, W3C. 2008.

6. Tzu-Yi Yu, Bharat K. Soni, Ming-Hsin Shih. Geometry Modeling and Grid Generation Using 3D NURBS Control Volume//NASA. Lewis Research Center, Surface Modeling, Grid Generation, and Related Issues in Computational Fluid Dynamic (CFD) Solutions. 1995. P. 491-503.

7. Piegl L., Tiller W. The NURBS Book. Springer, 1997.

САПР и графика 3`2010