Кластерная трассировка лучей в системах визуализации
В системах визуализации, используемых в САПР, таких как AutoCAD, 3ds max, ArchiCAD и других, применяются алгоритмы построения изображения, основанные на методе трассировки лучей или фотонов. Наиболее часто встречаются следующие виды трассировки: прямая трассировка лучей, обратная трассировка, трассировка фотонов, трассировка путей, двунаправленная трассировка путей, Metropolis Light Transport. Во всех случаях просчет изображения осуществляется по уравнению визуализации, представленному в виде суммы интегралов. Уравнение визуализации имеет следующий вид:
![]()
В частности, интеграл в уравнении визуализации удобно представить в виде суммы прямого и непрямого освещения:
![]()
![]()
![]() ,
,
где fr — функция двунаправленной распределения отражательной способности поверхности, Le — испущенное освещение, Li — освещение, приходящее на поверхность.
Непрямое освещение (Lindirect) — это любые отскоки лучей света после первого отскока. Непрямое освещение формирует основную часть освещения в реальном мире, в котором мы живем: зеркальное отражение света от поверхностей, диффузное рассеивание света, а также фокусирование света в результате отражения или преломления.
В рамках данной статьи мы будем рассматривать общее освещение в сцене как сумму первичного освещения и всего остального освещения — вторичного. В ходе проведенных опытов стало известно, что основную вычислительную нагрузку несет просчет вторичного освещения. Для каждого первичного луча при трассировке в идеале производится depth*samples проверок на пересечение с геометрией, где depth — глубина трассировки, samples — количество лучей, вновь генерируемых при каждом соударении с геометрией сцены. С ростом глубины трассировки доля вторичных отскоков растет с геометрической прогрессией. Таким образом, на просчет вторичного освещения уходит основная часть времени визуализации.
В ходе проведенных исследований было установлено, что основную часть времени визуализации занимают два типа операций: проверка на пересечение с геометрией сцены и функция затенения материала поверхности. Пропорции их влияния на время визуализации могут изменяться в зависимости от конкретной сцены.
В результате исследований было выявлено, что для сцен, используемых в архитектуре, характерной особенностью является большое количество примитивов геометрии в сцене. Соответственно время визуализации данных сцен будет сильно зависеть от скорости работы системы визуализации с геометрией сцены.
При трассировке луча в любой системе визуализации производится проверка на пересечение луча с примитивом для каждого луча. В данной статье возьмем наиболее распространенный и перспективный тип примитивов — треугольник.
Для каждого найденного пересечения луча с треугольником производится вычисление локальных координат внутри треугольника и получение цвета в данной точке из функции затенения материала данной поверхности. Операция проверки на пересечение с примитивом в существующих системах визуализации производится для каждого луча.
Среди уже существующих методов оптимизации работы с геометрией стоит выделить два наиболее эффективных: сортировка геометрии в kd-дерево до стадии трассировки и пакетная трассировка лучей. Использование хорошего kd-дерева позволяет достичь количества тестов на пересечение с треугольником в среднем до 1,1-1,4 (Chaosgroup Vray Demo v1.5) для каждого луча. Показатель количества тестов луча на пересечение с треугольником меньше единицы будет означать, что тест на пересечение с треугольником производится не для каждого луча. По опыту можно сказать, что в существующих системах визуализации такая ситуация недостижима.
Пакетная трассировка лучей объединила идею о повторном использовании геометрии данного участка сцены c аппаратным объединением лучей в группы с последующей трассировкой. Данный метод также позволяет сократить время визуализации, но пакетная трассировка показывает свою эффективность только для первичных лучей.
В данной статье предлагается подход, позволяющий находить в геометрии сцены кластеры треугольников и осуществлять трассировку группы лучей в случае, если кластер найден. Предполагается, что данный подход позволит достичь количества тестов на пересечение луча с треугольником меньше единицы.
Предлагается сортировать все лучи по их ориентации и положению в пространстве с целью выделить группы лучей, которые потенциально могут найти ближайшее пересечение со сценой с одним и тем же треугольником или группой треугольников. В случае если такая группа лучей будет найдена, необходимым и достаточным станет лишь нахождение локальных координат внутри треугольника, считая, что сам треугольник уже был найден.
В случае применения пространственных структур сортировки геометрии становится возможным использовать результат упорядочивания геометрии в пространстве с целью локализации поиска ближайшей геометрии. При трассировке луча или группы лучей, попадающих в некоторую область трехмерной сцены, данная локализация позволяет свести наборы проверок на пересечение луча с геометрией к поиску, касающемуся части глобального дерева поиска. В таком случае задача сводится к некоторому набору тестов на пересечение лишь для отдельной области сцены.
Рассмотрим два случая (рис. 1): типичный пример трассировки луча в сцену (а) и с использованием предлагаемого метода (б).
 a
a
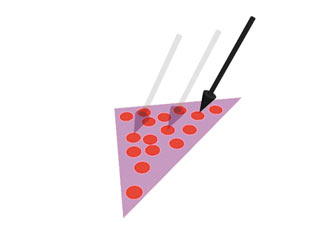 b
b
Рис. 1. Трассировка: а — классическая; б — кластерная
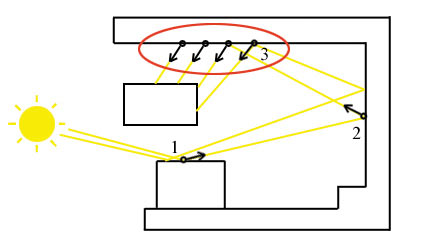
Рис. 2. Группирование лучей в кластеры
При трассировке вторичного луча в большинстве случаев находится новая точка пересечения со сценой, из которой далее генерируются несколько новых лучей. Рекурсия повторяется до тех пор, пока не будет достигнут один из критериев прекращения трассировки. Для любой глубины трассировки для всего множества точек расчета вторичного освещения имеем по нескольку лучей, сгенерированных согласно функции ДФОС материала данной поверхности.
В отличие от подходов, применяемых в современных системах визуализации, где лучи трассируются рекурсивно один за другим, предлагается лишь генерировать координаты новых лучей, а трассировку выполнять позднее. Принцип отложенной трассировки позволяет сказать, что мы имеем дело с некоторым набором векторов, имеющих свои координаты, где каждый вектор — это луч, сохраненный в виде набора данных, который пока не подвергся операции трассировки. Всё это подмножество таких векторов предлагается разделять на подклассы по признаку направления, где в один класс могут входить все векторы, направление которых не превышает данного телесного угла в общей для всего множества векторов системе координат. Другими словами, группа векторов — это набор векторов, указывающих примерно в одном и том же направлении с погрешностью ε. Для каждого сравнительно небольшого участка поверхности в сцене найдется некоторый набор лучей, указывающих примерно в одном и том же направлении (если отражательная функция ДФОС одинакова для всей площади данного участка поверхности). Следовательно, эти лучи или некоторая их часть вероятно попадут на одну и ту же поверхность при их трассировке.
Таким образом, лучи предлагается классифицировать по двум признакам:
- направление луча;
- начало луча.
Отличие предлагаемого метода от уже существующих подходов состоит в возможности объединять лучи в группы на любой глубине трассировки луча, а также в возможности адаптивного выбора количества создаваемых подгрупп при разбиении каждой группы трассируемых лучей.
Рис. 2 иллюстрирует группирование лучей в кластеры.
Алгоритм работы предлагаемого подхода выглядит следующим образом:
1. На каждом промежуточном шаге трассировки сортировать все лучи по направлению.
2. Разделить полученные группы лучей по признаку точки отсчета.
3. Проецировать для каждой полученной группы лучей пирамиду проецирования в направлении распространения данной группы лучей.
4. Выделять во временный массив все полигоны, оказавшиеся внутри пирамиды проецирования данной группы лучей.
5. Сортировать полигоны по их нормалям и положению в пространстве.
6. Поиск смежных полигонов, лежащих в одной плоскости.
7. Разбиение данной группы на подгруппы в соответствии с результатами сортировки геометрии (группа создается для данного треугольника либо для группы смежных треугольников, лежащих в одной плоскости).
8. Осуществить групповую трассировку всей группы лучей разом.
Таким образом, данный подход позволяет разбить задачу визуализации на нужное количество подзадач: появляется гибкий механизм распределения загрузки вычислительных ядер процессора. Каждую из полученных подзадач можно отдать на выполнение отдельному вычислительному модулю, способному производить арифметические и геометрические операции. Примерами таких модулей могут стать процессоры x86 персональных компьютеров, видеочипы от ATI и NVIDIA, поддерживающие вычисления общего назначения, а также высокопроизводительные компьютеры (серверы и кластерные системы). Разбиение задачи визуализации на некоторое множество кластеров позволяет гибко управлять загрузкой имеющихся вычислительных мощностей.
Преимуществом данного подхода является его гибкость и универсальность, поскольку его можно применять в любом из известных алгоритмов трассировки: в фотонной трассировке, при любых способах просчета глобального освещения и т.д. Стоит также отметить, что метод не влечет за собой абсолютно никаких ухудшений качества картинки, поскольку направлен на иную организацию способа расчета трассировки, без изменения принципа любого из существующих алгоритмов моделирования освещения.
Область применения предлагаемого метода: САПР, профессиональные пакеты 3D-моделирования и визуализации.


