Кластерная модель геометрического описания сложных объектов
C развитием компьютерной техники большое значение сегодня приобретают задачи математического моделирования сложных физико-химических процессов с целью оптимизации различных технологических процессов и задач. Это приводит к необходимости решения задач математической физики в геометрически сложных областях, причем такие физические характеристики объекта моделирования, как теплопроводность, плотность и др., могут зависеть и от времени, и от пространственных переменных.
Существующие подходы создания геометрических моделей в различных средах проектирования основаны на использовании классических геометрических фигур, их объединении и пересечении (конкатенации). Эти способы хорошо работают для простейших объектов, состоящих из двух-трех классических фигур — окружности, эллипса, прямоугольника и др. Однако сложные нерегулярные объекты, требующие большого количества описательных действий, представляют значительные трудности при создании программной модели. Например, создание компьютерной модели скальной горной породы (рис. 1) для задач моделирования неупругих деформаций (например, в двумерном случае) — непростая задача даже для профессиональных пользователей программных средств проектирования.

Рис. 1. Объект моделирования — скальная горная порода
Отдельной проблемой являются задачи модифицирования созданных объектов. При изменении сложной модели необходимо заново пройти всю цепочку ее создания, но только с новыми параметрами. Если же требуется сделать несколько модификаций, то здесь трудозатраты сравнимы с созданием нескольких различных моделей. Поэтому использование существующих программных средств проектирования геометрических объектов приводит к значительным временным затратам и требует высокой квалификации пользователей.
Принципиальное отличие предлагаемого подхода от имеющихся методов описания геометрических объектов состоит в том, что здесь пользователем задается не граничная область объекта, а его внутренние точки. В этом случае граничные точки объекта моделирования могут быть вычислены по определенным заданным алгоритмам в соответствии с указанными точками (несущие или кластерные элементы).
Данный метод описания, при котором геометрическая модель (и ее граница) образуется в результате взаимного объединения элементарных объектов, позволяет пользователю системы геометрического проектирования отмечать лишь отдельные базовые точки в генерируемой заранее сетке, а программная среда дает возможность сформировать весь объект целиком. Такой подход заметно упрощает процесс описания модели. Кроме того, моделирование с помощью кластерного подхода естественным образом позволяет задавать в области модели различные физические параметры (плотность, теплоемкость, теплопроводность и др.), которые ставятся в соответствие с несущими точками и распространяются на всю элементарную область.
Применение кластерной модели позволяет легко выполнять модификацию объекта путем смещения кластерных элементов или задания новых параметров для свойств кластера (базовых направлений, касательных, типов соединяющих линий и др.).
Кластерный способ описания геометрического объекта является и более естественным для неподготовленного пользователя, когда сложный пользовательский интерфейс разнообразных CAD/CAM-систем представляет значительные трудности для их применения при двух- и, особенно, трехмерном проектировании.
С математической точки зрения кластерная модель обеспечивает параметризацию континуальной пространственной области с помощью конечного множества независимых элементов. Каждый элемент, обладая определенными свойствами, позволяет формировать свою часть геометрической области.
Целью такой параметризации является минимизация хранимой информации о структуре объекта и обеспечение наиболее полного соответствия исходной геометрической области и модели, полученной в результате описания с помощью кластера.
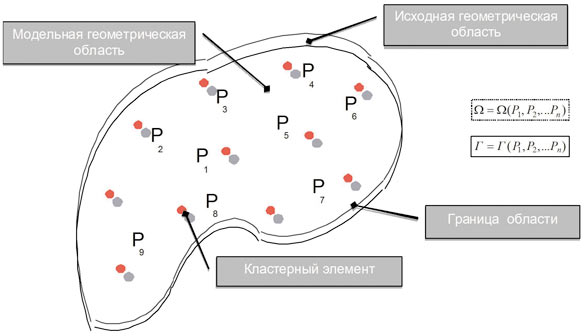
Рис. 2. Параметризация геометрической области
Параметризация произвольной области с помощью конечного набора элементов (рис. 2) может значительно сократить объем хранимой информации о ней и фактически является алгоритмом сжатия данных, что позволяет компактно хранить данные об объекте, передавать по каналам связи, а также проводить идентификацию объекта:
![]()
При описании объекта с помощью набора определяющих точек каждый элемент определяет область, сопоставимую с каждой из них, причем здесь учитываются топологические условия их взаимного расположения:
![]()
Для использования кластерного подхода необходимо ввести пустую сеточную область, в которой заданы пустые кластерные элементы и определено понятие соседнего кластера, то есть для каждого кластерного элемента определены четыре ближайшие базовые точки (двумерный случай).
При добавлении в пустую сеточную область нового элемента может формироваться новый кластер, определяемый правилами объединения кластера, или могут независимо существовать два независимых кластерных объекта. Условия, при которых из независимых кластеров формируется новый объект, существенным образом зависят от расположения кластерных элементов (расстояния между ними), а результирующий объект формируется при анализе топологии кластерных элементов (выделяются соседние кластерные элементы и применяются правила объединения).
На рис. 3 представлена структура элементарного кластера, применяемая для моделирования геометрической области. С помощью данной структуры кластерного элемента можно очень гибко и полно описать внутреннюю часть геометрической области и внешней границы моделируемого объекта.
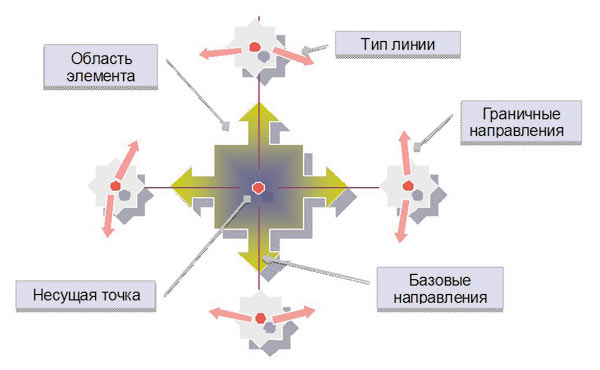
Рис. 3. Структура кластерного элемента
Представленная модель содержит информацию о четырех базовых направлениях и четырех граничных точках, каждая из которых включает данные по двум граничным направлениям. Кроме того, в классе, описывающем граничные направления, содержится информация о правилах объединения (типе соединяющей граничной линии). Таким образом, вид элементарной области, генерируемый несущей точкой, определяется 12 дополнительными параметрами:
![]()
где P = P(x, y) — координаты несущей точки, Gi = Gi(x, y) — векторы базовых направлений, DiLR = DiLR(x, y) — векторы, определяющие положение касательных направлений.
Описание типа соединяющей линии содержится в граничном элементе кластера, входящего в моделируемый объект, и может представлять собой:
- прямую линию;
- линию, образованную пересечением двух направлений;
- гладкую кривую, проходящую через две граничные точки и определяемую двумя направлениями.
Общая граница кластерной области состоит из набора таких простейших элементов границы, определенных для основных типов топологических структур, образующихся в кластере.
Вследствие того что кластерное представление предполагает возможность автоматического построения геометрической области, пользователю предлагается возможность интерактивного задания правил группирования, перемещения несущих и граничных точек, изменения касательных направлений и др.
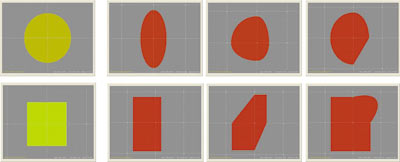
Отличительной особенностью кластерного подхода является то, что при создании классических геометрических фигур на такой плоскости, как окружность, эллипс, квадрат, прямоугольник и др., достаточно кластера всего из одного элемента (рис. 4).
Рис. 4. Одноэлементный кластер
На рис. 4 видно, что одноэлементый кластер можно рассматривать как обобщение классических геометрических фигур на плоскости, что дает пользователю предлагаемой среды простые, интуитивно понятные средства их создания и модификации.
В разработанной интерактивной программной среде (CLASTERS) при создании окружности или квадрата пользователь должен указать одну точку из пустой сеточной области. При этом, в зависимости от параметров умолчания, хранящихся в выбранной несущей точке, будет сформирован соответствующий объект. Модифицирование полученного объекта также выполняется простыми интерактивными средствами. Например, чтобы изменить объект (круг или квадрат), достаточно выбрать направление (одно из четырех) и переместить вдоль него базовую граничную точку. При этом из квадрата будет получен прямоугольник, а из круга — эллипс. Если же задать другой тип соединяющей линии вдоль одного из граничных направлений, то будет получен урезанный эллипс или прямоугольник со сглаженным углом. Опция изменения граничных направлений предоставляет пользователю возможность создать из круга фигуру с более сложной формой, чем эллипс, а из квадрата — произвольный четырехугольник.
Таким образом, предлагаемая структура кластерного элемента обеспечивает возможность единообразного описания весьма разнообразных геометрических фигур, благодаря чему достигаются универсальность и гибкость предлагаемого подхода кластерного моделирования.
Отдельно стоит вопрос построения гладкой границы кластера. Для этого была решена задача интерполяции, в которой заданными величинами являлись две точки и значения касательных в них. Задача интерполяции состояла в определении алгоритмической процедуры построения гладкой кривой, имеющей непрерывную производную по возможности наиболее высокого порядка и проходящей через заданные точки с заданными касательными.
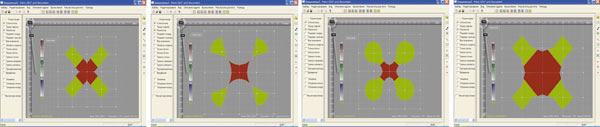
Представленный на рис. 5 пятиэлементный кластер показывает возможности предлагаемого подхода по созданию более сложных фигур. Данный подход позволяет путем выбора небольшого количества элементов сформировать довольно сложную модель и, проводя ее модификацию, получить весьма интересные объекты.
Рис. 5. Пятиэлементный кластер
Несмотря на то что внешний вид полученных объектов сильно отличается от исходной модели, топологические свойства в каждом объекте остаются неизменными (сохраняются связи между несущими точками в кластере): центральная точка непосредственно соединена с четырьмя точками, а остальные точки — только с одной, центральной.
Кластерный подход дает широкие возможности для экспериментирования с созданными объектами. Изменение свойств кластерных элементов, входящих в модель, приводит к довольно неожиданным геометрическим фигурам, которые заранее представить довольно сложно, но при этом исходный объект остается узнаваемым. Эти свойства кластерного подхода могут быть использованы в различных дизайнерских моделях (в частности, в промышленном дизайне), когда требуется создать новую форму на основе уже заданного прототипа.
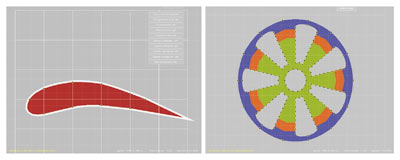
Разработанная программная среда, основанная на кластерном подходе, может применяться и для моделирования различных технических объектов, причем интуитивно понятный интерфейс позволяет выполнять такие построения даже неподготовленному пользователю (рис. 6).
Рис. 6. Технические объекты в среде кластерного моделирования
Обладая определенными физическими свойствами (например, цветом), заданными в несущей точке, кластерный элемент выявляет некоторую область, которая автоматически наделяется теми же свойствами, что и сам кластерный элемент. Такой подход в большой мере упрощает процесс описания геометрической модели и задание в ней различных физических характеристик, а также является определяющим условием при задании различных сеточных разбиений и выполнении расчетов на основе разработанной модели.
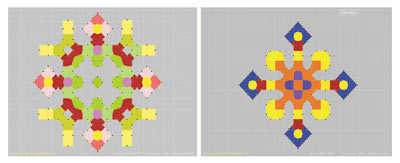
Кластерная модель обладает рядом преимуществ по сравнению с известными классическими подходами при описании объектов со сложной нерегулярной границей (рис. 7). Например, для того чтобы создать показанные на рис. 7 объекты с помощью разработанной программной среды, пользователю необходимо лишь выбрать определенное количество несущих точек и переопределить в них кластерные свойства.
Рис. 7. Сложный многоэлементый кластерный объект