Внутренний программный модуль определения габаритов 3D-моделей для системы Unigraphics

Владимир Тихомиров

Unigraphics (UGS) — известная на мировом рынке CAD/CAM/CAE-система и достаточно мощный инструмент для построения трехмерных моделей. Однако невозможно создать продукт, который бы решал все запросы пользователей, поэтому во многих CAD-системах, в частности в UGS, присутствует механизм, с помощью которого квалифицированный программист может разрабатывать собственные встраиваемые в систему программные модули, решающие нужные пользователю задачи. К таким механизмам в UGS относятся программирование с применением функций Open API UGS [1].

При использовании Open API открываются расширенные возможности автоматизации [2] моделирования и обработки 2D- и 3D-объектов благодаря набору библиотек и подпрограмм, позволя-ющих внешнему (или внутреннему) приложению получить доступ к объектам модели UGS.

На производстве при работе с системой UGS появилась необходимость определения габаритов 3D-моделей, создаваемых в этой системе. Выяснилось, что такая функция в UGS не предусмотрена, и пользователь тратил время на анализ детали, построение дополнительных объектов и вычисление расстояний. Задача пользователя усложнялась в случае, если требовалось проведение измерений составных деталей и сборочных единиц.

В современных CAD-системах обычно нет инструментов для нахождения минимальных габаритов созданных 3D-моделей. Тем не менее необходимость получения этих данных очевидна — взять хотя бы задачу о проектировании упаковки для изделия или раскрое материала в заготовительно-штамповочном производстве.

Проблема автоматизации определения габаритов 3D-моделей в CAD-системах неоднократно поднималась на страницах специализированных изданий [3]. Каждый автор решал эту задачу по-своему. Но все предложенные в настоящее время решения имеют весьма тяжеловесные алгоритмы, требующие длительного времени выполнения на компьютере. Для практического применения в повседневной работе технолога это неприемлемо.

В статье подробно разбирается алгоритм и его программная реализация (на языке С) авторского программного модуля для определения минимальных габаритов 3D-моделей деталей в среде CAD-системы Unigraphics. Модуль успешно используется на машиностроительных предприятиях.

В настоящей статье приведен пример автоматизации некоторой конструкторско-технологической задачи за счет применения встроенных инструментов программирования CAD-системы Unigraphics. В Интернете (не говоря уже о русскоязычной литературе) найти подобные примеры на данный момент весьма затруднительно, в то время как интерес к этим технологиям автоматизации проектировочных работ непрерывно растет. При этом автор полагает, что читатель знаком с основами технологии Open API Unigraphics [4].

Постановка задачи

В любой CAD-системе имеются программные функции, которые определяют габариты создаваемой в системе модели (объекта), но выполняют эту операцию в текущей системе рабочих координат (WCS) (рис. 1а), в которой деталь может располагаться по-разному, а значит, по-разному определяются CAD-системой ее габариты (рис. 1б).

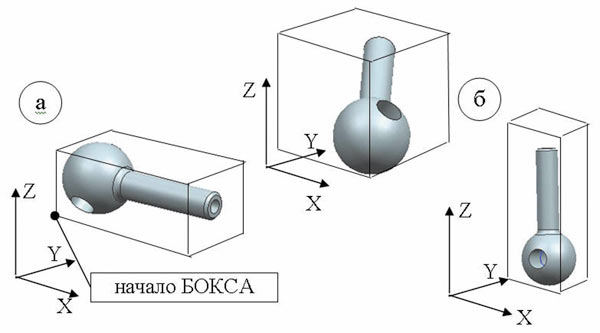
Рис. 1. Вид габаритных БОКСов в WCS при разном положении объекта

Параллелепипед, образованный полученными габаритами и охватывающий модель, будем называть БОКС. Объем БОКСа — критерий, определяющий оптимальность найденных габаритов. Задача разрабатываемого программного модуля — найти габариты заданного объекта (или группы объектов), имеющие минимальный объем БОКСа. Такие габариты будем называть минимальными габаритами объекта.

Разработка внутреннего модуля Unigraphics

Пользовательские программные модули в системе Unigraphics можно создавать на языке С в среде Visual Studio. Программист, используя прилагаемые к Unigraphics библиотеки функций Open API, создает DLL-модуль, который затем запускается из среды Unigraphics на исполнение. Такие программные модули называются внутренними.

Построим внутренний программный модуль UGS, который решает задачу нахождения минимальных габаритов для твердого тела, выбранного на рабочей сцене UGS. Сценарий работы модуля простой:

1. Пользователь запускает модуль, появляется диалог выбора твердого тела.

2. Пользователь выбирает (мышью) нужное тело на сцене.

3. Программа производит поиск бокса с минимальными размерами, но полностью вмещающего в себя выбранное тело.

4. Программа печатает в информационном окне системы длину, ширину и высоту найденного бокса.

Центральной функцией, которая будет помогать нам в поиске минимальных габаритов, является:

UF_MODL_ask_bounding_box_exact(…).

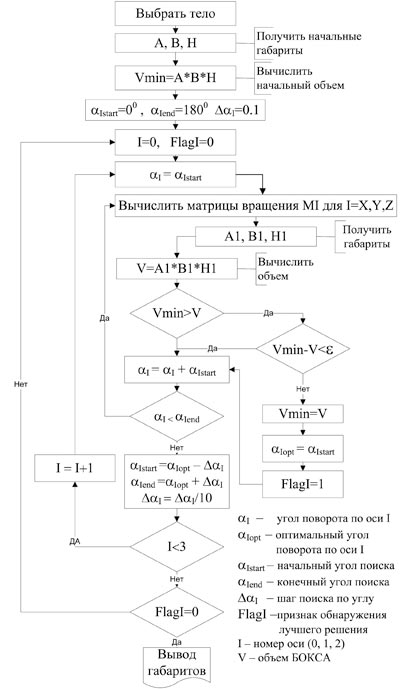
Рис. 2. Алгоритм поиска минимальных габаритов тела

Эта функция определяет габариты указанного объекта в текущей системе рабочих координат UGS. Функция принимает следующие входные параметры:

• первый — тэг объекта тела, для которого строится БОКС габаритов;
• второй — тэг системы координат, в которой строится БОКС.

Затем идут выходные параметры:

• третий — координаты точки «начала» БОКСа габаритов (см. рис. 1);
• четвертый — массив единичных векторов, определяющих направление трех ребер габаритного бокса, выходящих из точки «начала»;
• пятый — массив длин этих трех ребер бокса.

Если получаемые из функции длины ребер обозначить через dX, dY и dZ, то объем построенного бокса (V) определяется как их произведение и в процессе поиска нужного нам ответа должен стремиться к минимуму:

V = dX · dY · dZ -> min   (1)

По существу, перед нами стоит оптимизационная задача. Решим ее методом сужающегося перебора. Для этого предлагается следующий алгоритм (рис. 2):

• в цикле производится поворот текущей системы координат вокруг оси X с шагом Δα от αStart = 0°до αEnd = 180° и на каждом шаге определяется габаритный бокс. По формуле (1) вычисляется текущий объем бокса и запоминается угол αMin, при котором этот объем минимален. По завершении цикла система координат разворачивается нaа запомненный угол с минимальным объемом бокса;
• такой же цикл выполняется для оси Y, а затем для оси Z;
• далее начальный угол поиска назначается как:

   αStart = αmin – Δα,

   а конечный как:

   αEnd = αmin + Δα;

• шаг поиска Δα уменьшается в 10 раз, и описанные циклы повторяются снова. Далее по тем же принципам снова изменяются углы начала, окончания и шаг поиска. И всё это продолжается, пока на очередном витке программа не сможет найти бокса с объемом меньше, чем на предыдущем витке, или новый найденный объем не будет отличаться от старого на величину заданной точности (для расчетов точность вычисления объема ε примем равной 0,0001 мм3);
• после того как это событие произойдет, программа распечатывает размеры найденного минимального бокса.

Программный код, реализующий описанный алгоритм, представлен в листинге 1.

/* Модуль поиска минимальных габаритов заданного тела  */

#include

//Назначаем используемые файлы описаний функций Open API UGS

#include

#include

#include

//назначим тэг выбираемого объекта (глобальная переменная)

tag_t object;

//точка входа главного программного модуля

extern DllExport void ufsta(char *param, int *returnCode, int rlen)

{  //данные к диалогу выбора тела

 char* message=”Выберите твердое тело”;

 char * title=”Заголовок”;

 int response;

 int scope=UF_UI_SEL_SCOPE_WORK_PART;

 double cursor[3];

 char mes[131];   //строка для текстовых сообщений

 int FlagI=0,  //флаг наличия нового минимального решения

      n;  //индекс цикла расчетов по осям

 double  osZ[3]={0,0,1},  //вектор направления оси X

      osX[3]={1,0,0},  //вектор направления оси Y

      osY[3]={0,1,0};  //вектор направления оси Z

 double center[3]={0,100,0};  //точка начала координат

 tag_t view, teg_wcs, csys_id;  //тэги систем координат

 double  mtxP[9],  //матрица вращения вокруг оси X

      mtyP[9],  //матрица вращения вокруг оси Y

      mtzP[9],  //матрица вращения вокруг оси Z

      mt1[9],  //матрица промежуточного произведения

      mt[9];  //суммарная матрица вращения

 //массивы для получения стандартного габаритного БОКСА

 double min_corner[3];

 double directions[3][3];

 double distances[3];

 double Vmin, //минимальный объем БОКСА

 //оптимальные углы поворота координат по осям:

 UGmin[3]={0,0,0}, //начальные значения — 0 радиан

 Vnew; //текущий расчетный объем БОКСА

 //текущие углы поворота координат по осям

   double ugol[3]={0,0,0};

 //начальные углы поворота по осям при поиске в радианах

   double start[3]={0, 0, 0},

  //конечные углы поворота по осям при поиске в радианах

   end[3]={PI, PI, PI},

  //шаг изменения углов по осям при поиске (в радианах)

   shag[3]={0.1, 0.1, 0.1};

 //инициализация Open API. Если ошибка — выход из программы

 if(UF_initialize()) return;

/* выбрать объект для определения минимальных габаритов. Здесь использована функция, создающая стандартный диалог для выбора объекта на сцене UGS */

 UF_UI_select_with_single_dialog(message,title, scope,

 solid_init_proc, NULL, &response, &object, cursor,&view );

//получить текущие габариты выбранного объекта

 UF_MODL_ask_bounding_box_exact (object, NULL_TAG, min_corner, directions, distances);

//определить объем начального габаритного БОКСа и принять его за минимальный

 Vmin=distances[0]*distances[1]*distances[2];

//начать цикл поиска минимальных габаритов

 do{

//флаг признака нахождения новых оптимальных габаритов принять за 0

 FlagI=0;

//выполнить цикл перебора по трем осям

 for(n=0; n<3; n++){

/* выполнить цикл перебора поворота оси от стартового угла до конечного для каждой оси n, где 0-ось X, 1-ось Y, 2-ось Z */

for (ugol[n]=start[n]; ugol[n]<=end[n]; ugol[n]+=shag[n])

 {

/* рассчитать матрицы поворота отдельно по каждой оси. Применяемая функция берет матрицу mt…P), и пересчитывает ее элементы, поворачивая векторы матрицы на угол (ugol[…]) вокруг заданной оси (os…) */

 UF_MTX3_rotate_about_axis( osX, ugol[0], mtxP);

 UF_MTX3_rotate_about_axis( osY, ugol[1], mtyP);

 UF_MTX3_rotate_about_axis( osZ, ugol[2], mtzP);

/* вычислить общую матрицу поворота координатной системы. Выполняется с помощью функций перемножения матриц */

 UF_MTX3_multiply(mtxP, mtyP, mt1);

 UF_MTX3_multiply(mt1, mtzP, mt);

//получим тэг матрицы очередного поворота координат

 UF_CSYS_create_matrix(mt, &teg_wcs);

/* создать местную систему координат в указанной опорной точке и с указанной матрицей поворота */

 UF_CSYS_create_csys(center, teg_wcs, &csys_id);

//получить габаритный БОКС в новой системе координат

 UF_MODL_ask_bounding_box_exact(object, csys_id,

  min_corner, directions, distances);

//вычислить объем нового БОКСа

 Vnew=distances[0]*distances[1]*distances[2];

/* если текущий объем меньше минимального и разница их больше точности вычислений (назначена 0.0001 мм3), то: */

 if ((Vmin>Vnew) && (Vmin-Vnew)>0.0001) {

 Vmin=Vnew;   //запомнить новый объем,

 UGmin[n]=ugol[n]; //запомнить новый угол,

 FlagI=1; //установить флаг этого события

 }

//удалить объект — новую систему координат

 UF_OBJ_delete_object(csys_id);

 }

//после окончания перебора всех углов поворота

ugol[n]=UGmin[n];// найденный оптимальный угол запомнить

         }//конец трех циклов вращения по осям

//установить новые границы и шаги поиска

 for (n=0; n<3; n++)

 {start[n]=ugol[n]-shag[n];

  end[n]=ugol[n]+shag[n];

  shag[n]/=10;

 }

//повторять циклы вращения осей, пока обнаруживается новое минимальное решение (FlagI=1)

 } while (FlagI); //конец цикла do

/*из цикла вышли, значит решение найдено,

 осталось вывести результаты на экран. Для этого прорисуем на экране найденный БОКС. Для чего предварительно надо повернуть систему координат в найденное оптимальное положение, а для этого следует: определить матрицы вращения для найденных оптимальных углов */

 UF_MTX3_rotate_about_axis( osX, ugol[0], mtxP);

 UF_MTX3_rotate_about_axis( osY, ugol[1], mtyP);

 UF_MTX3_rotate_about_axis( osZ, ugol[2], mtzP);

//рассчитать оптимальную суммарную матрицу вращения

 UF_MTX3_multiply(mtxP, mtyP, mt1);

 UF_MTX3_multiply(mt1, mtzP, mt);

//получить тэг оптимальной матрицы

 UF_CSYS_create_matrix(mt, &teg_wcs);

/* создать местную систему координат в указанной опорной точке и с найденной оптимальной матрицей поворота */

 UF_CSYS_create_csys(center, teg_wcs, &csys_id);

//в этой системе определить оптимальный габаритный БОКС

 UF_MODL_ask_bounding_box_exact (object, csys_id,

  min_corner, directions, distances);

//и, наконец, выполнить процедуру визуализации этого БОКСа на экране

 BoundBox(min_corner,directions,distances);

//открыть информационное окно системы

 UF_UI_open_listing_window();

//подготовить текстовую строку с результатами для вывода

 sprintf(mes,»Габариты объекта: \n(%8.2f х %8.2f x %8.2f)мм\n»,

  distances[0], distances[1], distances[2]);

//вывести размеры бокса в информационном окне системы UGS

 UF_UI_write_listing_window(mes);

//удалить объект — созданную систему координат

 UF_OBJ_delete_object(csys_id);

//снять подсветку (выделение) с выбранного тела

 UF_DISP_set_highlight(object,0);

//закрыть библиотеку Open API

 UF_terminate();

}// конец главного программного модуля

//процедура точки входа завершения приложения

extern int ufusr_ask_unload( void ){

 return( UF_UNLOAD_IMMEDIATELY );}

Программа начинается с вызова функции выбора твердого тела на рабочей сцене: UF_UI_select_with_single_dialog(…). Интересной особенностью этой функции является использование в четвертом параметре процедуры обратного вызова, чтобы задать маску выбора тела. Такая технология назначения маски существенно повышает гибкость работы функции и позволяет задавать самые замысловатые алгоритмы изменения маски фильтра выбора в момент работы функции. Для нашего случая процедура обратного вызова проста и имеет вид, приведенный в листинге 2.

/* процедура обратного вызова назначения маски для функции выбора тела на входе в процедуру, обязательные параметры:

первый — адрес структуры маски выбора;

второй — указатель на дополнительные данные, передаваемые в процедуру (мы ничего не передаем, поэтому второй параметр вызова функции выбора тела у нас будет равен NULL */

int  solid_init_proc(UF_UI_selection_p_t select, void* user_data)

{

 int  ret_code;    //код возврата (ошибки)

 int  num_triples=1;  //количество структур масок выбора тела (одна)

 //маска на выбор твердого тела

 UF_UI_mask_t  mask_triples[]={UF_solid_type,0,0};

 //регистрация маски в системе UGS

 ret_code=UF_UI_set_sel_mask(select,

 UF_UI_SEL_MASK_CLEAR_AND_ENABLE_SPECIFIC,

 num_triples, mask_triples);

 //если все прошло успешно, вернуть УСПЕХ

 if(ret_code==0)return UF_UI_SEL_SUCCESS;

 //в противном случае вернуть ОШИБКА

 return UF_UI_SEL_FAILURE;

}

Далее в программе вводится переменная FlagI, которая приобретает значение 1, если программа нашла новое минимальное решение для габаритного БОКСа. Начинаются циклы, описанные в алгоритме поиска решения. Общая матрица вращения системы координат определяется как произведение матриц вращений по каждой оси отдельно. Циклы заканчиваются, если переменная FlagI к концу циклов осталась равной 0, то есть не было найдено ни одного нового решения.

Визуализация найденного оптимального габаритного БОКСа проводится процедурой BoundBox(…). Текст процедуры представлен в листинге 3.

/* Процедура вычерчивания габаритного БОКСа временными линиями

 На входе:

min_corner — координаты начальной точки БОКСа

directions — массив направлений трех базовых ребер БОКСа

distances —  массив длин базовых ребер БОКСа

*/

void BoundBox(double min_corner[3],

 double directions[3][3],double distances[3])

{  double p_N[10][3];  //массив точек углов БОКСа

    int i, j, k;  //индексы циклов

  tag_t work_view;  //тэг области просмотра

//структура свойств области просмотра

 UF_OBJ_disp_props_t props;

//заполнить структуру свойств области просмотра объекта текущими данными

UF_OBJ_ask_display_properties(object, &props);

//изменить цвет отображения временных линий на «бурый»

props.color=148;

//получить тэг области просмотра

UF_VIEW_ask_work_view(&work_view);

//прочертить базовые три ребра БОКСА

for (i=0; i<3; i++)

 { //для этого вычислить координаты конечной точки текущего ребра

UF_VEC3_affine_comb(min_corner, distances[i],

 directions[i],p_N[i]);

//чертить текущее ребро от начальной точки до конечной (расчетной)

UF_DISP_display_temporary_line(work_view,

 UF_DISP_USE_WORK_VIEW, min_corner, p_N[i], &props);

 }

//из концов построенных ребер строим еще ребра (по два)

k=3;

for (j=0; j<3; j++)

  for (i=0; i<3; i++)

  if (j != i) {/* если индекс ребра и индекс направления

   совпадают, такое ребро не строим */

UF_VEC3_affine_comb(p_N[j], distances[i],

  directions[i], p_N[k]);

UF_DISP_display_temporary_line(work_view,

 UF_DISP_USE_WORK_VIEW, p_N[j], p_N[k], &props);

   k++;

         }

//рассчитываем координаты последнего, самого удаленного узла

UF_VEC3_affine_comb(p_N[7], distances[1],

 directions[1], p_N[k]);

//и дочерчиваем оставшиеся три ребра

UF_DISP_display_temporary_line(work_view,

 UF_DISP_USE_WORK_VIEW, p_N[7], p_N[k], &props);

UF_DISP_display_temporary_line(work_view,

 UF_DISP_USE_WORK_VIEW, p_N[k], p_N[3], &props);

UF_DISP_display_temporary_line(work_view,

 UF_DISP_USE_WORK_VIEW, p_N[k], p_N[6], &props);

}

В процедуре для вычисления положения точки на заданном расстоянии и направлении от другой точки применена функция:

UF_VEC3_affine_comb(…). В ней четыре входных параметра: координаты исходной точки, величина дистанции до расчетной точки, вектор направления расчета, выходной параметр один — координаты новой рассчитанной точки.

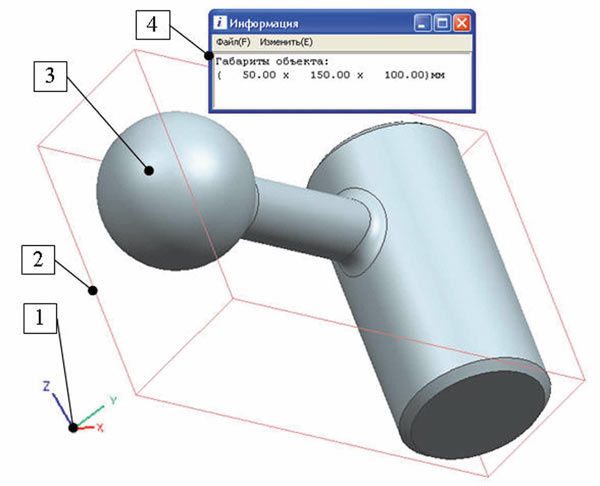
Рис. 3. Результат работы модуля определения минимальных габаритов

Для прорисовки временных линий (эти линии на сцене UGS существуют, пока пользователь не нажмет клавишу F5) используется функция UF_DISP_display_temporary_line(…) из раздела Open API дисплейных объектов. Первый параметр у нее — тэг видеообласти, в которой следует проводить отрисовку (удобно получать с текущей сцены функцией UF_VIEW_ask_work_view(…)), а последний — структура свойств отображения объекта (props), которая может быть либо заполнена вручную, либо, как у нас в процедуре, снята с одного из объектов сцены функцией UF_OBJ_ask_display_properties(…). В этой структуре, кстати, в поле props.color хранится цвет отрисовываемого объекта. Мы его задали бурым (индекс 148), но вы можете изменить его по своему усмотрению (индекс цвета меняется от 1 до 216).

Для проверки работы модуля подберите 3D-модель тела сложной конфигурации, к тому же развернутую по всем осям относительно рабочей системы координат. Запустите модуль, выберите объект и подождите от 10 до 40 секунд. Результат работы программы показан на рис. 3.

Из рисунка видно, что исходное тело 3 было развернуто в рабочей системе координат 1 на неизвестные углы. Тем не менее программа определила оптимальные углы разворота системы координат, чтобы получить минимальный БОКС — 2, и выдала информационное окно 4 с измеренными габаритами, (которые на 100% совпадают с реальными данными детали по конструкторской документации). Вы можете провес-ти тестирование модуля на своих примерах и убедиться в его высокой эффективности.

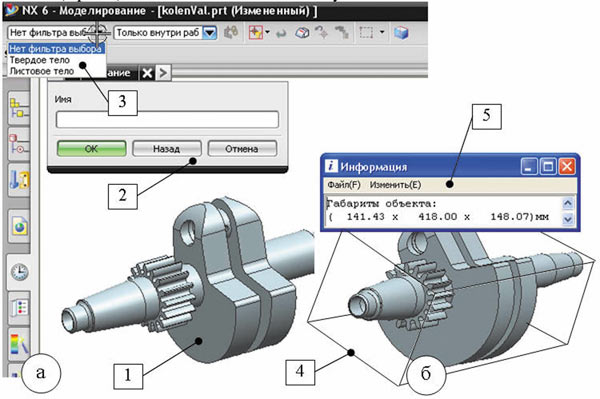
Рис. 4. Меню выбора объекта для определения габаритов

Для использования откомпилированного модуля (DLL) необходимо запустить Unigraphics, загрузить в него 3D-модель (1 на рис. 4), габариты которой следует определить, включить загрузку пользовательских DLL (Ctrl+U) и выбрать в открывшемся окне откомпилированный модуль. Модуль запустится на выполнение, и на сцене UGS появится диалог выбора объекта (2 на рис. 4). В поле фильтров (3 на рис. 4) можно конкретизировать тип выбираемого объекта (твердое или листовое тело), после чего следует мышью выбрать нужный объект (1 на рис. 4) и нажать на диалоге кнопку Оk.

Через некоторое время на экране появится информационное окно (5 на рис. 4) с результатами решения, и временными линиями будет визуализирован найденный минимальный БОКС объекта (4 на рис. 4).

Для тестирования разработанного приложения было взято 30 различных твердотельных 3D-моделей.

Экспертным путем для каждой модели были установлены ожидаемые минимальные габариты. По ним определен минимальный ожидаемый объем (Vож) охватывающего БОКСа. Затем все выбранные модели были пропущены через разработанный модуль определения минимальных габаритов и по ним был рассчитан реальный минимальный объем (Vр) охватывающего БОКСа. Полученные результаты представлены на рис. 5.

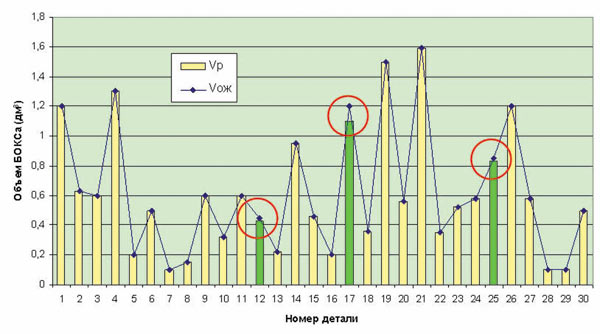
Рис. 5. Ожидаемые и полученные по программе объемы минимальных охватывающих БОКСов

Как видно из рисунка, программа в основном дала результаты, соответствующие экспертным оценкам, а в ряде случаев (выделено кружками) даже улучшила их (в среднем на 3-5%), предложив не увиденное экспертом решение. Так, на детали, представленной на рис. 6 и собранной из цилиндра (d = 20, h = 100) и конуса (D = 50, H = 80), оптимальным оказался не «очевидный» для эксперта параллелепипед 50x50x180, где сборка располагается «прямо» (см. рис. 6а), а несколько меньший по объему — 49,45x49,45x178,09, где сборка компонуется «наклонно» (см. рис. 6б).

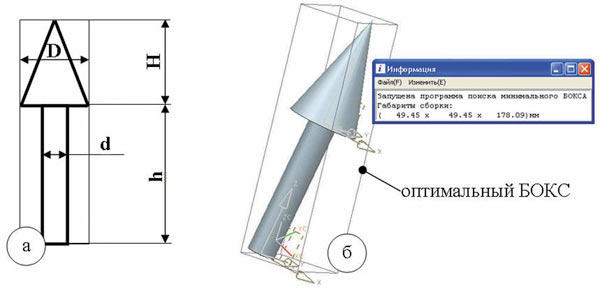
Рис. 6. Формирование габаритного БОКСа в программе

Аналогичная ситуация наблюдалась и на более сложном объекте (рис. 7). Программа определила, что наклонная упаковка исследуемого объекта занимает на 6% меньше места, чем «стандартная» прямая упаковка.

Заключение

Созданный внутренний модуль способен вычислять габариты как параметризованных, так и непараметризованных моделей. Это дает пользователю возможность измерить в CAD-системе Unigraphics габариты любой твердотельной 3D-модели, группы моделей или их сборок с минимальными затратами. Существует возможность определения габаритов отдельной грани (или нескольких граней) детали.

Модуль с успехом используется в технологических бюро Комсомольского­на-Амуре авиационного производственного объединения. Имеется акт о внедрении.

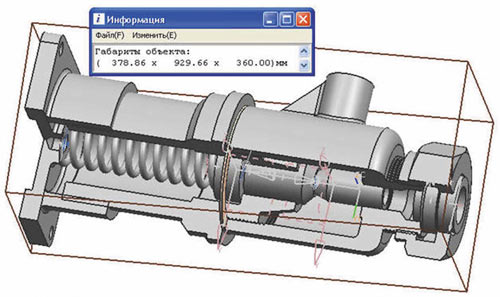
Рис. 7. Наклонная упаковка сложного объекта в минимальном БОКСе

Использованные источники

1. Краснов М. Unigraphics для профессионалов. М.: ЛОРИ, 2004. 141 с.

2. Куракин М. Повышение производительности работы с САПР// RM MAGAZINE. 2003. № 3.

3. Ермолин Е. Автоматическое определение минимальных габаритов деталей/ Е.Ермолин, М.Богданов, Р.Кусков, К.Лыков, А.Попова // САПР и графика. 2007.  № 12. С. 24-28.

4. Unigraphics NX — программирование//ESG.SPB.RU: сервер группы компаний бюро ESG. 2010. URL: http://www.esg.spb.ru/win /Pr_products/ Unigraphics/Unigraphics_NX/UG_program.htm (дата обращения: 30.03.2010).

---

Владимир Тихомиров

Канд. техн. наук, доцент, зав. кафедрой МОПЭВМ Комсомольского-на-Амуре государственного технического университета.

САПР и графика 7`2010