Оптимизация положения элементов механизированного крыла с использованием программных комплексов FlowVision-HPC и IOSO

Анастасия Шишаева (Начальник группы тестирования OOO «ТЕСИС»)
Игорь Москалёв (Инженер OOO «ТЕСИС»)
Сергей Жлуктов (Начальник группы мат. физики OOO «ТЕСИС»)
Андрей Аксёнов (Технический директор OOO «ТЕСИС»)
Юрий Бабий (Директор ЗАO «Сигма Технология»)
Игорь Егоров (Генеральный директор ЗАO «Сигма Технология»)
Виталий Судаков (Старший научный сотрудник Отделения аэродинамики ЦАГИ)

Введение

Важнейшее значение в аэродинамическом проектировании элементов летательного аппарата и всей компоновки в целом в настоящее время имеет вычислительная аэродинамика. Многие задачи, которые раньше решались только путем проведения длительных и дорогостоящих экспериментов в аэродинамических трубах, сейчас возложены на численный эксперимент. Современные достижения в развитии методов вычислительной аэродинамики позволили изменить процесс аэродинамического проектирования. За счет даже простого увеличения количества рассматриваемых альтернативных вариантов геометрии можно существенно улучшить ее характеристики, но гораздо больший эффект достигается путем использования специализированных процедур проектирования и анализа, включающих оптимизационные методы.

Решение задачи численной оптимизации базируется на интеграции двух компонентов: аэродинамического расчета и инструментария оптимизации. В настоящей работе описан разработанный программный продукт, который позволяет проводить оптимизацию различных конфигураций. При этом прямой аэродинамический расчет осуществляется в программном комплексе FlowVision-HPC, решающем задачи турбулентного течения жидкостей и газов в рамках осредненных по Рейнольдсу уравнений Навье — Стокса. Краткое описание этого комплекса дано в п. 1. Тестирование FlowVision-HPC на известном примере обтекания механизированного крыла с фюзеляжем (рис. 1) и сравнение с экспериментальными данными [1] приведено в п. 3. Форма крыла и экспериментальные данные взяты на сайте http://hiliftpw.larc.nasa.gov/index.html [1]. Сайт был специально создан для того, чтобы разработчики программ вычислительной аэродинамики могли сравнивать результаты своих расчетов с экспериментальными данными.

Рис. 1. Механизированное крыло в аэродинамической трубе [1]

Для решения дальнейшей задачи оптимизации аэродинамической формы используется программный комплекс IOSO, описание которого приведено в п. 2. В данной статье в качестве примера функционирования разработанного программного комплекса решается оптимизационная задача, цель которой — найти положения предкрылка и закрылка механизированного крыла [1], дающие максимальную подъемную силу и максимальное аэродинамическое качество при фиксированном положении центральной части крыла.

Работа выполнена при поддержке Министерства образования и науки Российской Федерации.

1. Программный комплекс FlowVision-HPC

В основу программного комплекса FlowVision положен метод конечных объемов. Расчетная сетка FlowVision — декартова, локально адаптивная. Локальная динамическая адаптация начальной сетки производится в соответствии с заданными пользователем критериями. Начальная сетка состоит из прямоугольных ячеек, но вблизи границы расчетной области происходит булево вычитание нерасчетных объемов из прямоугольных ячеек и образование произвольных расчетных многогранников [2]. При этом граница может иметь сложную криволинейную форму. Авторы работы [2] дали такой сетке название «сетка с подсеточным разрешением», поскольку никакого упрощения приграничных ячеек-многогранников не производится. Это кардинально отличает технологию FlowVision от технологии генерации расчетной сетки, известной как метод cut-cell, которая заменяет границу в ячейке плоским многоугольником. Несмотря на геометрическую сложность расчетной сетки FlowVision, порядок аппроксимации решаемых уравнений по пространству — второй. Это достигается использованием высокоточной расчетной схемы с реконструкцией решения внутри ячейки [3]. Уравнения движения жидкости решаются с помощью неявной схемы расщепления [2]. Алгебраические уравнения, возникающие при аппроксимации уравнений движения жидкости, энергии, переноса контактной поверхности, переноса турбулентных характеристик и пр., решаются методами крыловского типа. Программный комплекс FlowVision-HPC работает на компьютерах, имеющих смешанную архитектуру, совмещая межузловое MPI-распараллеливание с распараллеливанием по потокам в узле, как на компьютере с общей памятью. Применение смешанного распараллеливания позволяет добиться высококачественного масштабирования программного комплекса при работе на большом числе процессоров [4 и 5].

Все представленные результаты получены с использованием стандартной k-e-модели турбулентности [6] и новой подсеточной модели турбулентности для пристенных ячеек, недавно реализованной в FlowVision-HPC.

2. Программный комплекс IOSO

Программный комплекс многокритериальной оптимизации IOSO предназначен для решения сложных задач поиска оптимума при большом количестве критериев (при многокритериальной постановке), варьируемых переменных и ограничений, а также при сложной топологии целевой функции и при наличии областей невычисляемости [7].

Алгоритмы оптимизации IOSO базируются на новой эволюционной технологии построения поверхности отклика. Поэтому стратегия решения оптимизационных задач в IOSO существенно отличается от известных подходов нелинейного программирования: она обладает более высокой эффективностью и обеспечивает гораздо более широкие возможности [8 и 9].

В соответствии с логикой работы алгоритмов IOSO на каждой итерации осуществляется построение поверхностей отклика критериев оптимизации и ограничиваемых параметров. В процессе оптимизации используется информация, получаемая при исследовании поверхностей отклика, и накапливается информация об исследуемой системе в окрестностях оптимального решения. Это повышает адекватность (точность) поверхностей отклика в области экстремума.

Для построения поверхности отклика применяются различные высокоэффективные алгоритмы:

• адаптивные алгоритмы регрессионного анализа;
• эволюционные алгоритмы самоорганизации со структурно-параметрической аппроксимацией;
• алгоритмы нейронной сети.

При переходе от итерации к итерации используются процедуры изменения стратегии, которые осуществляют адаптацию параметров и структуры алгоритмов оптимизации применительно к конкретной решаемой оптимизационной задаче. В процессе оптимизации осуществляется следующая последовательность шагов:

1. Модификация плана эксперимента.
2. Адаптивное изменение текущей области поиска как по расположению в пространстве, так и по величине (moving strategy).
3. Адаптивный (без вмешательства пользователя) выбор типа (глобальная или локальная) и структуры поверхности отклика.
4. Уточнение поверхности отклика в текущей области экстремума.
5. Модификация параметров и структуры алгоритма оптимизации.

В отличие от известных технологий построения поверхности отклика, алгоритмы IOSO-технологии относятся к классу эволюционных процедур, которые адаптированы к проведению оптимизационных исследований и позволяют с высокой точностью предсказывать расположение эктремума в пространстве.

Таким образом, гибкая адаптивная структура эволюционного базового алгоритма технологии оптимизации IOSO обеспечивает существенное сокращение общего времени, необходимого для решения практических задач нелинейного программирования.

Проведенные исследования позволяют утверждать, что алгоритмы технологии оптимизации IOSO обладает следующими преимуществами:

• уверенно конкурируют с известными высокоэффективными методами оптимизации на классе гладких одноэкстремальных функций;
• инвариантны к различным классам задач оптимизации и могут использоваться при решении проблем условной и безусловной нелинейной оптимизации в однокритериальной и многокритериальной постановках с целевыми функциями различных типов;
• обладают хорошими глобальными свойствами и в большинстве случаев позволяют найти глобальный экстремум с высокой степенью вероятности;
• имеют высокую скорость сходимости и позволяют быстро и эффективно определять область экстремума в многомерных многоэкстремальных проблемах оптимизации;
• позволяют решать задачи стохастической оптимизации при высоком уровне шума/помех на критерий оптимизации и ограничения;
• являются чрезвычайно простыми в использовании при постановке и решении сложных практических проблем нелинейной оптимизации;
• имеют явное преимущество при решении других классов задач, часто встречающихся на практике: задач с недифференцируемой целевой функцией, многоэкстремальных задач, многоэкстремальных задач с невычисляемыми критериями оптимизации и ограничениями.

Программный продукт многокритериальной оптимизации IOSO NM работает под управлением OC Windows 2000/XP/7 и позволяет управлять расчетными моделями на удаленных компьютерах, работающих под управлением ОС Windows 2000/XP/7 и ОС семейства UNIX/Linux.

3. Сравнение с экспериментом

Рассматривается обтекание модели механизированного трехзвенного крыла с фюзеляжем (см. рис. 1) при следующих параметрах набегающего потока.

Условия:

α = 13°;

Re = 4 300 000;

М = 0,2;

T = 288,9 K.

Соответственно

V = 68,3 м с^-1;

p = 93 400 Па;

ρ = 1,12 кг м^-3;

m = 1,79·10^-5 кг м^-1 с^-1;

где:

α — угол атаки;

Re — число Рейнольдса;

М — число Маха;

T — температура;

V — скорость;

p — статическое давление;

ρ — плотность;

m — динамический коэффициент молекулярной вязкости.

Расчетная область показана на рис. 2. Рассматривается симмет-ричная постановка задачи. Детали модели представлены на рис. 3.

Рис. 2. Расчетная область

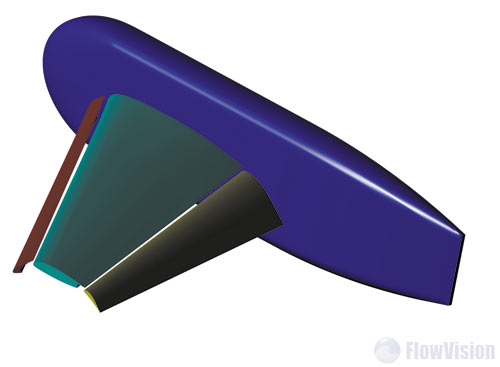
Рис. 3. Трехмерная модель обтекаемого крыла и фюзеляжа

Расчеты проводятся на двух сетках. В обоих проектах начальная сетка насчитывает около миллиона ячеек. Адаптация задается в объеме — внутри двух усеченных конусов до 1-го и 2-го уровней соответственно. Конусы охватывают предкрылок, основной элемент и закрылок (рис. 4 и 5). Кроме того, задается адаптация около поверхности трехзвенного крыла: в проекте с «Сеткой 1» — до 3-го уровня, в проекте с «Сеткой 2» — такая же адаптация до 3-го уровня и дополнительная адаптация до 4-го уровня. В процессе адаптации исходная ячейка разбивается на восемь равных частей, процедура повторяется до заданного уровня.

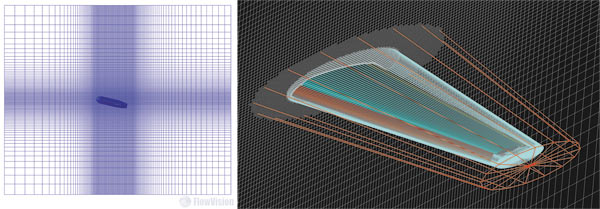
Рис. 4. Начальная сетка и объекты (усеченные конусы), в которых производится адаптация сетки

Рис. 5. Адаптация в проектах с «Сеткой 1» (слева) и «Сеткой 2» (справа)

В табл. 1 представлены значения коэффициентов сопротивления и подъемной силы, полученные в ходе расчетов, которые сравниваются с экспериментальными данными [1].

На рис. 6 можно видеть распределение предельных линий тока около поверхности модели, а на рис. 7 — распределение давления.

Полученное хорошее совпадение с экспериментальными данными говорит о том, что FlowVision-HPC можно использовать для решения прямых задач (расчета течения около фиксированной геометрической модели) в процессе решения задачи поиска оптимальной геометрической формы объекта.

Рис. 6. Распределение скорости по поверхности модели

Рис. 7. Распределение давления по поверхности модели

4. Решение оптимизационной задачи

Рассматривается компоновка самолета, состоящая из фюзеляжа и трехзвенного крыла. Механизация крыла состоит из выдвижного предкрылка и однощелевого выдвижного закрылка. В задаче фиксированными являются:

• форма фюзеляжа;
• положение и форма центральной (неподвижной) части механизированного крыла;
• форма крыла (с прижатой механизацией);
• формы сечений предкрылка и закрылка;
• угол атаки.

Переменными оптимизации являются положения предкрылка и закрылка относительно профиля крыла. Необходимо найти следующие шесть оптимальных параметров (рис. 8):

• угол отклонения предкрылка δ_S;
• горизонтальное смещение предкрылка x_S;
• вертикальное смещение предкрылка y_S;
• угол отклонения закрылка δ_F;
• горизонтальное смещение закрылка x_F;
• вертикальное смещение закрылка y_F.

Критериями оптимизации являются коэффициент подъемной силы Cy (необходимо найти его максимальное значение) и аэродинамическое качество профиля  Cy/Cx (необходимо найти его максимальное значение).

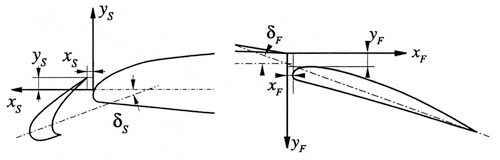
Рис. 8. Параметры оптимизации трехзвенного крыла

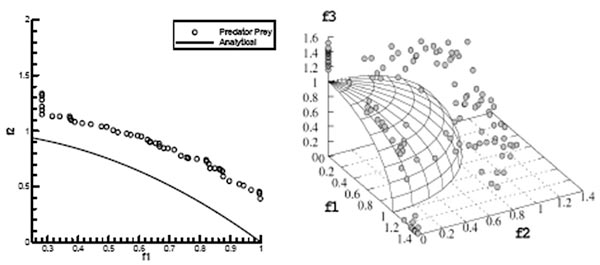
Рис. 9. Примеры Парето-множества для двухкритериальной и трехкритериальной задач (все критерии минимизируются)

Парето­множество — это множество неулучшаемых (по критериям) решений, каждому из которых соответствует свой набор оптимизационных (проектных) параметров. Парето­множество обеспечивает компромисс между критериями для недоминантного решения: один критерий улучшается, другой ухудшается. Для двухкритериальной задачи Парето­множество может быть представлено в виде двумерной зависимости, показывающей компромисс между критериями (по оси абсцисс — один критерий, по оси ординат — другой). Если критериев три, то Парето­множество может быть представлено в виде трехмерной поверхности в координатах критериев, которая показывает имеющийся компромисс между рассматриваемыми критериями. При этом каждой точке Парето­множества соответствует свой набор проектных (оптимизируемых) параметров. Практическая ценность Парето­множества заключается в том, что разработчик имеет объективную информацию об имеющемся компромиссе между критериями (рис. 9). На основе этой информации он может сделать обоснованный выбор оптимального проекта с учетом характера взаимного изменения критериев.

Таблица 1. Коэффициенты сопротивления и подъемной силы трехзвенного крыла

От аналогов программный комплекс IOSO отличает то, что в результате решения задачи оптимизации в многокритериальной постановке пользователь получает заданное им число Парето­оптимальных решений, равномерно распределенных в пространстве критериев. При решении поставленной оптимизационной задачи с использованием программных комплексов FlowVision-HPC и IOSO потребовалось всего лишь 350 различных вариантов положений предкрылка и закрылка для решения задачи оптимизации. В результате было определено 20 Парето­оптимальных точек — проектов системы «крыло­предкрылок-закрылок», различающихся конфигурацией. Это наглядно демонстрирует высокую эффективность инструментария IOSO NM, поскольку в случае применения известных технологий многокритериальной оптимизации для решения подобной задачи нужно решить тысячи прямых задач [10 и 11]. На рис. 10 полученное Парето­множество представлено в виде графика. Точка 1 соответствует максимуму аэродинамического качества, точка 3 — максимуму коэффициента подъемной силы, а точка 2 — максимальному значению аэродинамического качества при фиксированном значении коэффициента подъемной силы 1,65. Положения предкрылка и закрылка для точек 1, 2 и 3 представлены на рис. 11. Значения параметров оптимизации в этих точках приведены в табл. 2.

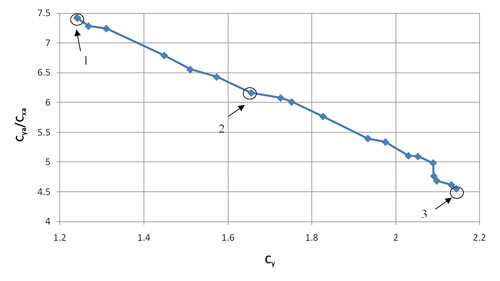
Рис. 10. Парето-множество: 1 — максимум аэродинамического качества; 2 — максимальное значение аэродинамического качества при коэффициенте подъемной силы 1,65; 3 — максимум коэффициента подъемной силы

Рис. 11. Конфигурации механизированного крыла: 1 — максимум аэродинамического качества; 2 — максимальное значение аэродинамического качества при коэффициенте подъемной силы 1,65; 3 — максимум коэффициента подъемной силы

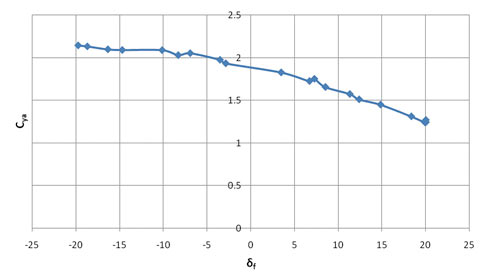
Рис. 12. Зависимость коэффициента подъемной силы Cya от угла отклонения закрылка δF

Из шести параметров наибольшее влияние на коэффициент подъемной силы и аэродинамическое качество оказывает угол отклонения закрылка dF (рис. 12 и 13). Влияние остальных параметров менее существенно.

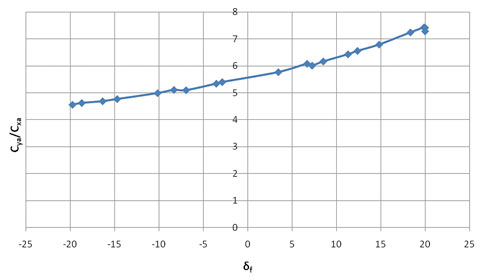
Рис. 13. Зависимость аэродинамического качества Cya/Cxa от угла отклонения закрылка δF

Заключение

Программный комплекс FlowVision-HPC был протестирован на известной задаче, опубликованной на сайте [1] . Расчеты течения воздуха около трехзвенного крыла показали хорошее совпадение с экспериментальными данными: на сетке из 3,7 млн ячеек расхождение с экспериментом по коэффициенту сопротивления получилось +1,8%, по коэффициенту подъемной силы — –2,6%. Это говорит о достоверности результатов, получаемых в FlowVision-HPC, и целесообразности его применения для решения прямых аэродинамических задач в процессе поиска оптимальной формы проектируемого объекта.

Создана связка программных комплексов FlowVision-HPC и IOSO NM, которая была использована для определения оптимального положения предкрылка и закрылка механизированного крыла. Получено Парето­множество оптимальных конфигураций механизированного крыла. Результаты решения оптимизационной задачи в многокритериальной постановке демонстрируют высокую эффективность программного продукта IOSO NM для данного класса задач.

Расчеты показали, что наибольшее влияние на подъемную силу и силу сопротивления оказывает угол отклонения закрылка.

Литература

1. http://hiliftpw.larc.nasa.gov/index.html.
2. Aksenov A.A., Dyadkin A.A., Pokhilko V.I. Overcoming of Barrier between CAD and CFD by Modified Finite Volume Method // Proc. of «1998 ASME Pressure Vessels and Piping Division Conference», San Diego, ASME PVP — 1998. V. 377­1.
3. Aksenov A.A., Gudzovsky A.V., Serebrov A.A. Electrohydrodynamic Instability of Fluid Jet in Microgravity // Proc. of 5th Int. Symposium on Computational Fluid Dynamics (ISCFD), Aug. 31 — Sept. 3, 1993, Sendai, Japan, Japan Society of Computational Fluid Dynamics — 1993. V. 1. p. 19­24.
4. Сушко Г.Б., Харченко С.А. Экспериментальное исследование на СКИФ МГУ «Чебышев» комбинированной MPI+threads реализации алгоритма решения систем линейных уравнений, возникающих во FlowVision при моделировании задач вычислительной гидродинамики // Труды международной научной конференции «Параллельные вычислительные технологии» (ПаВТ’2009), Нижний Новгород, 30 марта — 3 апреля 2009 г. Челябинск: Изд. ЮУрГУ, 2009. С. 316­324.
5. Харченко С.А. Влияние распараллеливания вычислений с поверхностными межпроцессорными границами на масштабируемость параллельного итерационного алгоритма решения систем линейных уравнений на примере уравнений вычислительной гидродинамики // Труды Международной научной конференции «Параллельные вычислительные технологии», Санкт­Петербург, 28 января — 1 февраля 2008 г. Челябинск: Изд­во ЮУрГУ, 2008. С. 494­499.
6. Wilcox D.C. Turbulence modeling for CFD // DCW Industries, Inc., 1994. 460 p.
7. Egorov I.N. Indirect Optimization Method on the Basis of Self­Organization // Curtin University of Technology, Optimization Techniques and Applications (ICOTA’98), Perth, Australia. 1998. V. 2. p. 683­691.
8. Egorov I.N., Kretinin G.V., Leshchenko I.A., Kuptzov S.V. IOSO Optimization Toolkit — Novel Software to Create Better Design // AIAA paper AIAA­2002­5514, 9th AIAA/ISSMO Symposium and Exibit on Multidisciplinary Analysis and Optimization, Atlanta, GA, 4­6 September 2002.
9. Egorov I.N., Kretinin G.V., Leshchenko I.A., Kuptzov S.V. Multi­Objective Robust Optimization Using IOSO Technology. Part I: Main Features // EUROGEN 2003, Barcelona, Spain, 15­17 September 2003.
10.  Akira Oyama, Meng­Sing Liou. A Multi­Stage Compressor Design Optimization Using CFD // The 8th Japan­Russia Joint Symposium on Computational Fluid Dynamics, 25 September 2003.
11. Kipouros T., Jaeggi D., Dawes B., Parks G. and Savill M. Multi­objective Optimisation of Turbomachinery Blades Using Tabu Search // Evolutionary Multi­Criterion Optimization, Third International Conference, EMO 2005, Guanajuato, Mexico, 9­11 March, Proceedings. 2005.

САПР и графика 9`2010