Компактное представление KD-дерева в системах трехмерной визуализации

Дмитрий Котов, Владимир Ланцов

В системах трехмерной визуализации, используемых в САПР, для повышения скорости визуализации применяется ряд различных способов, в том числе структуры пространственного разбиения и сортировки. Разновидностью таких структур является KD­дерево. В большинстве случаев это одна из наиболее эффективных структур пространственного разбиения и сортировки. Среди подходов представления KD­дерева в памяти ЭВМ стоит выделить метод, предложенный Ingo Wald [1], и метод, разработанный М. Шевцовым, А. Супиковым и А. Решетовым [2]. В методе [1] для представления узла KD­дерева требуется 64 бита информации. В методе [2] представлено расширение данного метода для реализации на x64­ платформе, а объем памяти для представления узла KD­дерева также равен 64 битам (или 8 байт на узел).

В методе [1] представление узла KD­дерева имеет следующий вид:

/* basic 8­byte layout for a kd­tree node */

struct KDTreeNode {

union{

//position of axis­aligned split plane

float split_position;

// or number of leaf primitives

unsigned int items;

}

unsigned int dim_offset_flag;

//’dim_offset_flag’ bits encode multiple data:

// bits[0..1]: encode the split plane dimension

// bits[2..30]: encode an unsigned address offset

// bit[31]: encodes whether node is an inner node or leaf

};

// macros for extracting node information

#define DIMENSION(n) (n­>dim_offset_flag & 0x3)

#define ISLEAF(n) (n­>dim_offset_flag & (UINT)(1<<31))

#define OFFSET(n) (n­>dim_offset_flag & 0x7FFFFFFC)

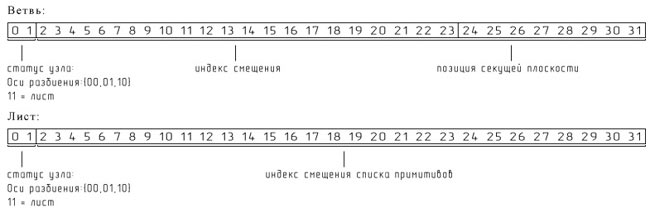
В предлагаемом в данной статье подходе для представления узла KD­дерева требуется 32 бита данных:

/* basic 4­byte layout for a kd­tree node */

struct KDTreeNode

{

 unsigned int dim_offset_split;

 //’dim_offset_split’ bits encode multiple data:

 // bits[0..1] : split plane dimension{00,01,10}, or leaf{11}

 // bits[2..24] : encode an unsigned address offset

 // bits[25­31] : encodes split plane position relative percentage

};

// macros for extracting node information

#define STATE (n) (n­>dim_offset_split & 0x3)

#define OFFSET(n) (n­>dim_offset_split & 0x3FFFFF80)

#define SPLIT (n) (n­>dim_offset_split & (UINT)(7<<31))

В рамках описания данного подхода будем условно называть неконечные узлы KD­дерева ветвями, а конечные узлы — листьями, тогда образ хранения информации об узле KD­дерева можно представить в таком виде, как показано на рисунке.

Количество битов для хранения смещения узла в глобальном массиве узлов KD­дерева равно значению максимальной глубины данного дерева. В ходе исследований было обнаружено, что максимальная скорость прохода луча по ускоряющей структуре достигается при глубине KD­дерева в 22­23 уровня, то есть 22­23 бита на индекс смещения узла KD­дерева. В ходе тестирования на проектах сцен, содержащих от нескольких тысяч до 11 млн примитивов (треугольников), было обнаружено, что дальнейшее увеличение глубины KD­дерева не дает существенного роста производительности (как в предлагаемом подходе, так и с использованием представления узла KD­дерева, как в подходе [1]) — он может составлять от 1 до 3%. При чрезмерно больших значениях глубины KD­дерева скорость визуализации имела тенденцию к снижению. Следует отметить, что размер значительного количества сцен, создаваемых при работе над проектом в САПР в направлениях архитектуры, дизайна, а также при создании трехмерных моделей инженерных и конструкторских разработок, находится ниже отметки 10 млн примитивов. Однако встречаются и проекты, содержащие от 100 млн до нескольких миллиардов примитивов, и с развитием той или иной отрасли, где применяются САПР, увеличивается и количество примитивов в проекте.

При глубине дерева, равной 23, на адресование листа в глобальном массиве листов требуется 22 разряда, что позволяет адресовать 4 194 304 листа. В хорошо сбалансированном KD­дереве лист содержит в среднем 2­4 примитива, следовательно, дерево с максимальной глубиной 23 примерно будет содержать до 16 777 000 примитивов. При необходимости дальнейшего увеличения максимальной емкости KD­дерева можно применять иерархию kd­поддеревьев. При 22­битном индексе листа остается 8 бит, которые можно использовать на адресацию новых поддеревьев, что позволяет адресовать свыше 273 млрд листов с сохранением возможности дальнейшего наращивания количества поддеревьев.

При прохождении по KD­дереву, построенному в соответствии с предложенным методом, размеры узлов дерева вычисляются итеративно, где значение позиции секущей плоскости, хранящееся в 7 битах при глубине дерева 23, указано в процентах относительно родительского узла, стоящего уровнем выше. При реализации данного метода прохождения по KD­дереву затраты на вычисление конкретных размеров узла можно сократить, используя опережающее вычисление размеров дочерних ячеек средствами блока потоковых вычислений (SIMD).

Таким образом, данный подход позволяет сократить объем памяти, занимаемой KD­деревом, на величину до 50%. Это позволит избежать обращения к файлу подкачки в отдельных случаях и разместить всю структуру KD­дерева в ОЗУ. Экономия затрат памяти является основной отличительной особенностью данного подхода. В случае его применения при визуализации проектов, созданных в САПР, в направлениях архитектуры, дизайна, а также инженерных и конструкторских разработок в условиях острой нехватки информационной емкости ОЗУ возможна ситуация, когда размещение всей структуры KD­дерева в памяти ОЗУ позволяет избежать значительного падения производительности по отношению к случаю, когда при нехватке памяти ОЗУ используется файл подкачки.

Библиография

1. Wald I. Realtime ray tracing and interactive global illumination: PhD thesis. Saarland University, 2004.
2. Shevtsov M., Soupikov A., Reshetov A. Efficient acceleration structures layout for rendering on 32­ and 64­bit many­core architectures. Intel Corp., Graphicon’2009.
3. Havran V. Heuristic Ray Shooting Algorithms: PhD thesis. Czech Technical University in Prague, 2001.

САПР и графика 11`2010