Конечно-элементный анализ для всех. Часть 2

Путем анализа вибраций конструкции можно детально проиллюстрировать поведение изделия под воздействием динамических нагрузок

Джордж Лайрд (George Laird)

В первой части статьи мы объяснили, что любая конструкция имеет нормальные частоты колебаний (собственные частоты колебаний) и что у этих нормальных частот, в свою очередь, есть специфические формы деформации (собственные формы, или нормальные формы колебаний). Мы также указали на то, как можно применять эту информацию в сфере проектирования, отметив, что несовпадение частот возбуждения с первыми двумя собственными частотами колебаний структуры обусловливает ее стабильность, как при статическом нагружении. Теперь мы хотели бы пойти дальше и продемонстрировать, как такую простую форму анализа можно эффективно использовать для выяснения поведения структуры при динамическом нагружении.

Доминанта: участие массы

Интересный факт: при анализе собственных форм колебаний мы можем сопоставить (увязать) процентную долю массы конструкции, колеблющейся по каждой из форм. Имея достаточное количество форм, вы задействуете 100% массы, однако для сложных конструкций понадобятся сотни форм. Принято считать, что если вам удастся задействовать 90% массы конструкции, то это уже хорошо. Сначала мы рассмотрим классический пример, а затем продемонстрируем, какое значение данная идея имеет для реального конструкторского мира.

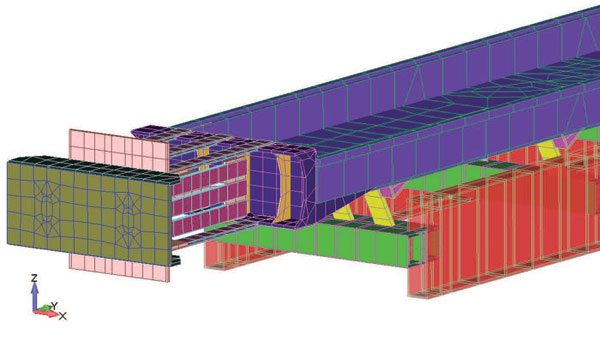
Рис. 1. Монтажные опоры двигателя виброконтейнера представляют собой массу гибких металлических пластин, выступающих за край конвейера. Желтым выделены пружины из стекловолокна, мотор не виден

Мы используем свободно опертую балку, так как ее легко изобразить, легко выразить в виде формул и, что самое главное — ее легко нарисовать на белой доске. На рис. 2 приведен небольшой пример первых трех форм колебаний свободно опертой балки и процентные доли ее массы, принимающие каждую из этих форм. Первая форма образуется чаще всего, ее формируют 82% массы балки, колеблющейся вверх и вниз. Лишь небольшая часть массы балки принимает вторую и третью формы, что абсолютно несущественно по сравнению с первой формой.

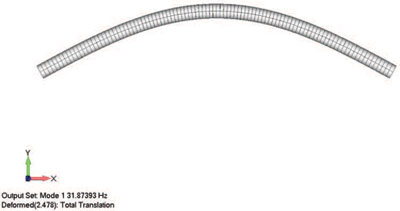
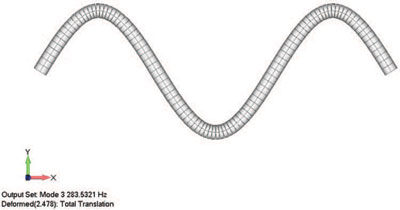
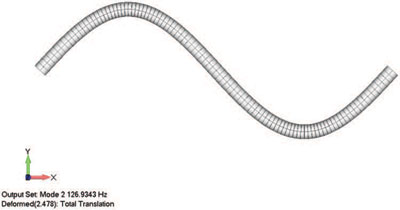
Рис. 2. Иллюстрация анализа вибраций опертой балки. Слева направо: первая форма собственных колебаний — форма деформации, в которой участвует 82% массы балки, двигаясь вверх и вниз; вторая и третья формы образуются только при гораздо больших частотах колебаний. Во второй форме участвует только 10% массы, в третьей — всего 3%. Эти формы практически не влияют на общее поведение структуры

Все перечисленные формы колебаний — однонаправленные. В реальности массовая доля обладает шестью степенями свободы в каждой конкретной собственной частоте. Это означает, что если мы окажем воздействие на первую форму в вертикальном направлении (направлении деления массы), то 82% массы структуры переместится вслед за этой формой. Если мыслить, как Ньютон, и исходить из того, что F = m·a, то мы сможем визуально представить преобладание данной формы и те огромные силы, которые могут возникнуть как отклик.

Транспортировка гороха

Давайте воспользуемся данной информацией для решения нескольких типичных технических задач. В промышленности используются вибрационные конвейеры для транспортировки сырья, начиная от стручков гороха и заканчивая древесным углем. Пример такого вибрационного конвейера показан на рис. 1. Он транспортирует стручки гороха по территории перерабатывающего предприятия. Движение происходит благодаря работе вибродвигателя, который создает синусоидально меняющуюся силу, ориентированную по продольной оси конвейера (оси Y). Эта сила заставляет конвейер скользить вперед и вверх по стекловолоконным рессорам.

Работая на своей резонансной частоте, конвейер подает горох вперед и вверх очень плавными толчками. Скорость транспортировки сырья определяется рабочей частотой, длиной и углом расположения стекловолоконного покрытия пружин.

Основной проблемой данного типа конвейера является то, что во время разогрева, когда вибромоторы набирают обороты, активизируются побочные формы колебаний, часто вызывая поломку конвейера до того, как он достигает требуемой рабочей частоты. Наш анализ собственных частот и форм колебаний показывает, что конвейер проходит три формы колебаний, прежде чем достигает рабочей частоты в 18 Гц. В таблице приведена краткая сводка данных, полученных в результате такого анализа.

Помимо этих числовых данных на рис. 3 показаны формы четырех колебаний. Теперь мы имеем полную картину поведения конвейерной системы в динамических условиях.

Хотя вибромотору и требуется пройти три формы колебаний для достижения требуемой рабочей частоты в 18 Гц, для него есть три благоприятных фактора: прикладываемая сила направлена по оси Y; доли массы, приходящиеся на первые три формы колебаний, очень малы (менее 6%); основные направления первых трех форм не совпадают с силовой (возмущающей) функцией. Таким образом, при помощи базового анализа собственных форм и частот колебаний можно протестировать конструкцию очень сложной инженерной системы.

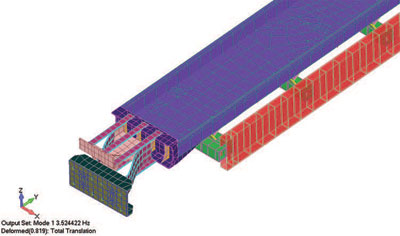
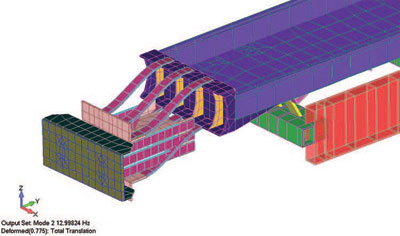
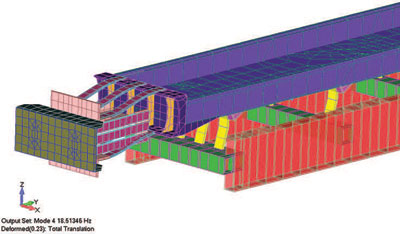
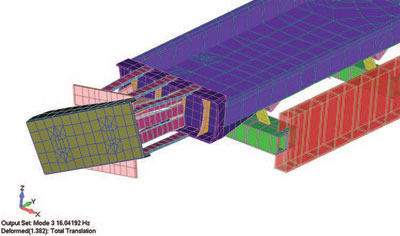
Рис. 3. Четыре формы собственных колебаний конвейерной ленты (слева направо, в порядке повышения частоты до достижения рабочего значения). На форму колебаний 1 при частоте 3,5 Гц приходится 5% массы по оси Х; на форму 2 — 5,8% по оси Z, третья форма на частоте 16 Гц имеет долю массы 1% по вращению оси Y, а на 4-ю форму, образующуюся на частоте 18 Гц, приходится 60% массы по оси Y

Результаты анализа собственных частот и форм колебаний

Что делает поездку в автомобиле плавной

Вы никогда не задумывались о том, что делает поездку в автомобиле такой плавной и приятной? Этот эффект связан с исключением форм колебаний, которые могут привести к резонансу, то есть с сохранением динамической устойчивости механических характеристик изделия.

Проводя анализ современного трейлера, представьте себе конечно-элементную модель с высокой степенью идеализации за счет использования балочных элементов для небольших трубок в конструкции, пластинчатых элементов для основных продольных трубок и множества массовых элементов для имитации двигателя, кондиционеров, топливных и водяных баков и пассажиров. По итогам анализа естественных форм колебаний мы получаем 45 частот в диапазоне от 2,3 до 15 Гц.

Не стоит пытаться понять, какая из форм колебаний может вызвать проблемы, не зная, какая доля массы приходится на каждую из этих форм. Чтобы всё упорядочить и избежать хаоса, мы можем графически изобразить суммарное распределение масс по осям Х, Y и Z.

Плавность движения зачастую представляет собой не что иное, как «прыжок» структуры, или скачок по оси Y. Самый большой интересующий нас скачок происходит в форме колебаний 21, когда доля массы, участвующая в образовании данной формы, резко возрастает с 21 до 43% (20% массы движется вперед в форме колебаний 21). Если мы исследуем эту форму колебаний более детально, то обнаружим, что весь корпус автомобиля движется вперед с частотой около 10 Гц. Теперь ясно, что частот порядка 10 Гц следует избегать.

К счастью, стандартный дорожный шум при движении автомобиля редко превышает частоту в 5 Гц. С учетом полученных знаний о поведении собственных форм колебаний и долях участия массы структуры в них мы можем рассчитывать на плавную и спокойную поездку.

Как проектировать более прочные конструкции

Одной из данностей анализа собственных форм колебаний является то, что вы не получаете никакой информации о масштабе произошедшего в реальности отклика (деформации или сжатия). Дело в том, что вы не прикладываете к структуре никакой нагрузки. Хотя это и налагает некоторые ограничения, мы можем использовать так называемую плотность энергии деформации, чтобы оценить, в каком месте структура наиболее податлива и уязвима.

Собственная форма колебаний конструкции представляет собой допустимую форму деформации, которая напрямую связана с моделью энергии деформации. Элементы со значительными показателями деформации — это те элементы, которые напрямую влияют на собственную частоту колебаний данной формы. Если вы сможете уменьшить энергию деформации, тогда вам удастся повысить эту частоту.

На рис. 4 показан корпус для электронного изделия, к которому крепится пара монтажных кронштейнов. Плотность энергии деформации для первой формы сосредоточена вокруг кронштейнов. В данной конструкции кронштейны закреплены болтами в С-каналах, которые служат для прикрепления к стене здания. Конструкторская задача состоит в том, чтобы изделие могло выдержать довольно сильное землетрясение (GR-63-Core спецификация зоны 4).

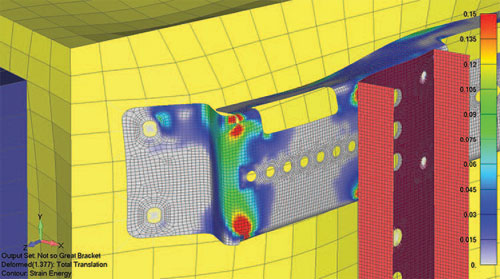
Рис. 4. Корпус для электронного изделия: а — плотность энергии деформации исходной конструкции монтажных кронштейнов корпуса для электроники, показывающая те области, которые, вероятнее всего, будут влиять на собственную частоту колебаний первой формы; б — кронштейн под воздействием имитации землетрясения (GR-63-Core спецификация зоны 4), показывающий высокую энергию деформации первой формы при частоте 7 Гц в точках перегиба кронштейна; в — измененная конструкция кронштейна с закрепленными концами имеет гораздо более низкую энергию деформации и повышает первую собственную частоту колебаний до 10 Гц

Для имитации землетрясения конструкцию раскачивают во всех трех направлениях. Первая форма колебаний при частоте 7 Гц имеет долю массы 45%, раскачивающуюся вперед-назад по оси Z, что соответствует высокой энергии деформации в точках перегиба кронштейна, как показано на рис. 4. Для того чтобы усовершенствовать данную конструкцию, нам нужно работать только над зонами с высокой энергией деформации. Работа заключается в заделывании концов кронштейна. Когда кронштейн укреплен таким образом, энергия деформации уменьшается (как показано на рис. 3), а частота колебаний возрастает до 10 Гц.

Основы проведения углубленного анализа собственных форм колебаний

Не паникуйте, если полученные вами собственные частоты колебаний примерно равны рабочим частотам. Значение имеют только те собственные частоты, на которые приходятся значительные доли массы структуры. Собственные формы колебаний имеют направления, так же как и участвующие доли массы. Внимательно изучите эти направления и проверьте, соответствуют ли они направлению вашей силовой функции. Если не соответствуют (допустим, они ортогональны), тогда структура останется динамически устойчивой.

Если вам требуется усилить вашу конструкцию, взгляните на те формы, в которых участвует больше массы, а затем вычислите плотность энергии их деформации. Измените вашу конструкцию так, чтобы снизить плотность энергии деформации в зонах повышенной энергии деформации, и вы получите значительное повышение частот собственных колебаний вашей конструкции.

Будьте методичны и рассматривайте вашу конструкцию со всех сторон. Секрет создания динамически стабильной структуры состоит в том, чтобы учесть и собрать всё воедино: собственные частоты (частоты колебаний), формы колебаний (то есть формы деформации), доли участия массы в них; направления участвующей массы; плотность энергии деформации. Если вы будете осведомлены обо всех этих факторах, то, скорее всего, избежите неприятных сюрпризов в виде аномального поведения или разрушения вашей конструкции в условиях действия динамических нагрузок.

Продолжение в следующем номере.

www.siemens.ru/plm

Copyright © by Level 5 Communications, Inc., 1283 Main St., Dublin, NH 03444, All Rights Reserved. www.deskeng.com

САПР и графика 1`2011