Применение SYSWELD для исследования сварочных деформаций

Георгий Биленко
Инженер технической поддержки (отдел инженерного анализа), ООО «Делкам-Урал», Екатеринбург

Вступление

В настоящее время, вследствие постоянного прогресса в области автоматизированных вычислительных средств, численных методов и программных алгоритмов, в результате приближения мощных коммерческих программных комплексов к нуждам рядовых пользователей, компьютерный инженерный анализ (computer aided engineering, CAE) становится важной и неотъемлемой частью технологических процессов производства. В данной статье мы рассмотрим типичный случай применения программного комплекса SYSWELD от ESI Group для исследования сварочных деформаций в зависимости от закрепления конструкции.

При сварке деталей возникает напряженно-деформированное состояние (НДС), которое, как правило, изменяет исходные размеры конструкции, что в ряде случаев приводит к несоответствию с требованиями конструкторской документации (КД). Такие конструкции отправляются на доработку, требующую дополнительных слесарных операций, или просто выбраковываются. Чтобы уменьшить процент брака, проводят ряд экспериментов, в результате которых выявляется наиболее выгодная позиция закрепления конструкции с точки зрения сокращения деформаций. Достойной альтернативой этого дорогостоящего способа являются инженерные расчеты механики деформированного твердого тела. В этом случае расчет нескольких вариантов позволяет выбрать оптимальное размещение зажимов, обеспечивающее коробление заданных КД допусков.

Качество и быстрота компьютерного расчета во многом определяются выбором программы. В нашем случае осознанно применялся SYSWELD, поскольку этот уникальный программный продукт специально предназначен для моделирования процессов сварки различных типов.

Краткая справка о программном обеспечении

Данный пример показывает, как с помощью решений от компании ESI Group можно оптимизировать технологию. В качестве решателя и препроцессора применялся комплекс SYSWELD, в качестве постпроцессора — программа Visual Viewer.

Программа SYSWELD была разработана в 1970-х годах в недрах Министерства атомной промышленности Франции, а затем передана для коммерциализации французской фирме FRAMASOFT S.A., подразделению компании FRAMATOME, которая является известным разработчиком технологий, применяемых в атомной энергетике. Фирма FRAMASOFT S.A. сделала из SYSWELD мощный пакет программ виртуального моделирования сварки и термообработки для самых разных областей применения (рис. 1).

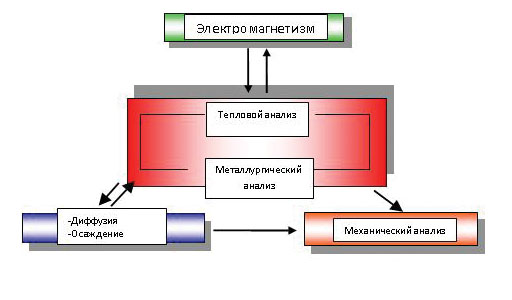
Рис. 1. Принципиальная схема работы SYSWELD

SYSWELD — мощный комплекс программ, содержащий несколько модулей:

• Welding Wizard — моделирует все физические процессы, происходящие во время сварки;
• Heat treatment — моделирует все физические процессы, происходящие во время термообработки;
• Sysweld Assembly — модуль сборки, используемый для моделирования сборки и сварки больших конструкций. Он оперирует переданными из предыдущих модулей величинами (поля напряжений и деформаций) для создания единого НДС всей конструкции.

Описание задачи

Наша задача состоит в том, чтобы провести исследование влияния условий закрепления на НДС после сварки. Сварка конструкции выполняется в трех возможных позициях, результаты по которым качественно и количественно различаются. Требуется выбрать вариант, при котором коробления и остаточные напряжения будут минимальны. Если такой вариант не будет найден, оптимальным вариантом будет считаться тот, где коробления будут минимальны.

CAD-модель конструкции представлена на рис. 2.

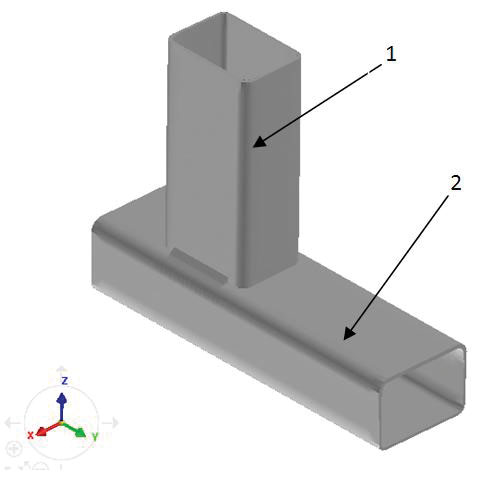
Рис. 2. CAD-модель изделия: 1 — верхний профиль; 2 — нижний профиль

Конструкция представляет собой два алюминиевых профиля, соединяемых между собой сваркой.

Используется алюминиевый сплав системы AlMnSi.

Для решения этой задачи применяется программный модуль Welding Wizard. Он содержит удобные пользовательские оболочки препроцессора и постпроцессора, с помощью которых можно относительно быстро поставить задачу сварки.

В Welding Wizard доступно несколько вариантов моделирования:

• расчетная модель объекта, построенная на основе как трех-, так и двумерных конечных элементов;
• модель объекта, построенная на основе только трехмерных конечных элементов;
• модель на основе только двумерных элементов.

В нашей задаче используется первый вариант моделирования.

На первом этапе выполняется решение тепло-металлургической задачи. В ее рамках требуется определить теплофизические характеристики стали, а также задать термокинетическую диаграмму зависимости металлургических фаз от скоростей охлаждения образца данного сплава.

С помощью программного кода происходит связывание точек выпадения фаз с температурой нагрева и скоростью охлаждения. Далее по данным тепло-металлургической задачи решается задача механики.

Исходными технологическими данными для решения тепловой задачи стали:

• порядок выполнения швов (рис. 3);
• свойства материалов.

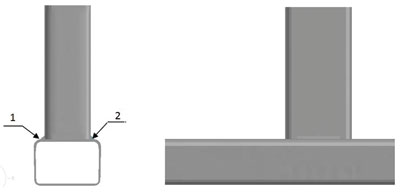
Рис. 3. Схема выполнения швов (цифры показывают очередность швов)

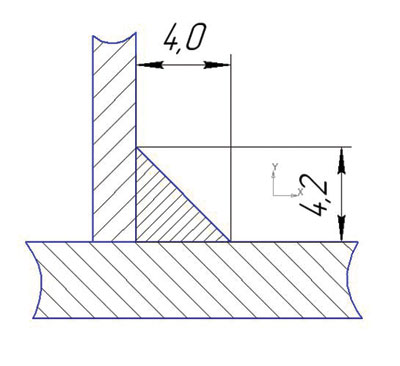
Рис. 4. Геометрические размеры сварного шва

Режим сварки выбирается исходя из геометрии сварного шва, которая была задана конструктором. Геометрия представлена на рис. 4.

Сначала требуется определить сварочный ток, напряжение, скорость сварки, которые обеспечат равномерное плавление и отсутствие прожога основного металла. Для этого используется специальный инструмент, встроенный в SYSWELD, — heat input fitting (рис. 5). В частности, он позволяет задать граничные условия для тепловой задачи, а также аналитическую модель распределения тепловой мощности источника.

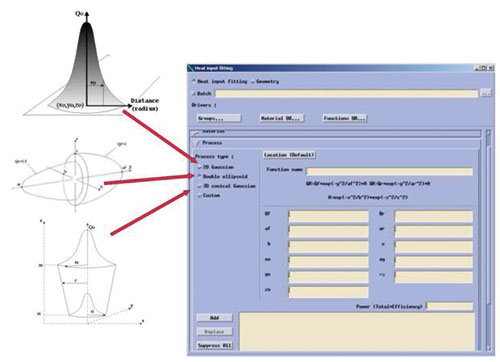
Рис. 5. Встроенный инструмент heat input fitting

По умолчанию нам доступно несколько аналитических моделей нагрева для описания сварочной ванны, а также граничных условий (ГУ). ГУ может быть задано изотермической или адиабатической границей, а также условием полного теплообмена: конвекцией и излучением из сварочной ванны расплавленного металла.

В данном случае используется аналитическая модель объемного тепловыделения двойного эллипсоида Голдака. Вот ее уравнения:

,

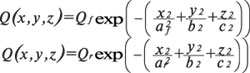где Qf,r — объемное тепловыделение, Вт/мм3, аf, ar, b, с — геометрические характеристики модели, мм.

Полезная мощность определяется как тройной интеграл по объему фигуры:

.

После того как определены геометрические параметры модели нагрева и задана величина максимального объемного тепловыделения, производится приближенный расчет при постоянных теплофизических характеристиках.

Далее задаются граничные условия теплообмена. В данном случае это условие третьего рода — полный теплообмен: конвекция и лучистый теплообмен.

Коэффициент лучистого теплообмена задается выражением:

f(t) = sigxex(t + to)(t² + to²),

где e = 0,8 — коэффициент излучения (степень черноты поверхности детали), sig = = 5,67x10^-8 — постоянная Стефана Больцмана; to = 20 °С — начальная температура среды (в нашем случае на поверхности тела), t — температура тела, °С.

Коэффициент конвективного теплообмена задается постоянным значением 2,5x10 ^-5 Вт/мм2.

Для решения задачи теплопроводности также требуется ввод необходимых данных для используемого материала: теплопроводность, l, Вт/ммxК; плотность, r, кг/мм3; теплоемкость, с, Дж/кгxК.

Все необходимые для моделирования свойства материала задаются в виде кусочно-линейных функций, показанных на рис. 6.

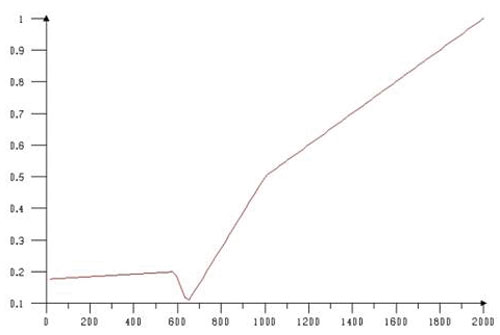
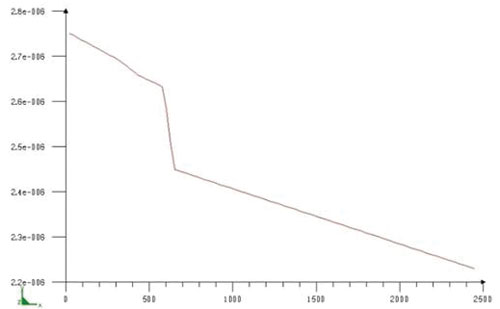
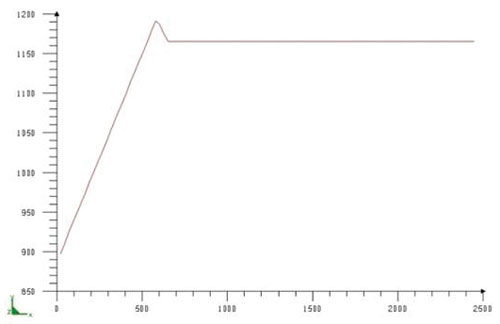
Рис. 6. Теплофизические характеристики: а — функция теплопроводности в зависимости от температуры; б — функция плотности в зависимости от температуры; в — функция теплоемкости в зависимости от температуры

Результатом вышеописанных операций является определение требуемой мощности источника, скорости его передвижения и формы сварочной ванны. Зная мощность, мы легко найдем сварочный ток и напряжение. Эти величины связаны следующей формулой:

Q = IxUxn,

где I — сварочный ток, I = 120 А; U — напряжение дуги, U = 30 В; n — КПД источника, n = 0,75.

По результатам решения стационарной тепловой задачи скорость сварки составила 12 мм/с.

После того как определены скорость сварки, ток и напряжение, переходим к расчету нестационарной тепловой задачи.

Результаты по распределениям тепловых полей показаны на рис. 7 и 8.

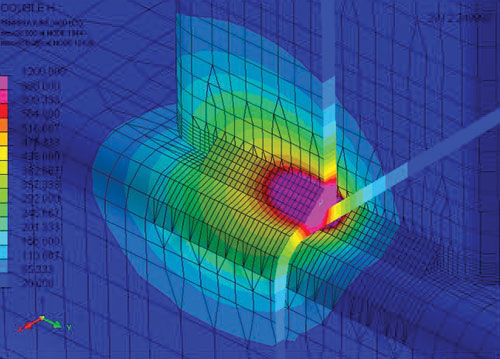
Рис. 7. Распределение тепловых полей для первого прохода на 3-й секунде

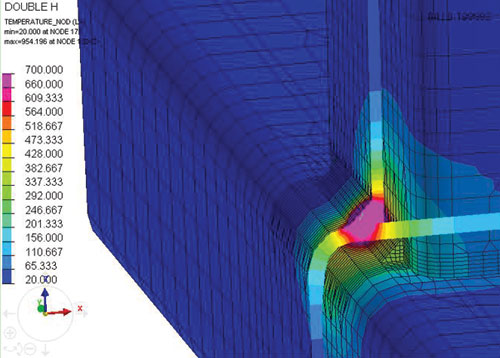
Рис. 8. Распределение тепловых полей для второго прохода на 8-й секунде

1-й проход: t нач = 0 с, t кон = 4,5 с, Vсв = 12 мм/с, Q = 3000 Вт.

2-й проход: t нач = 6 с, t кон = 11 с, Vсв = 12 мм/с, Q = 3000 Вт.

Одновременно с тепловой задачей решается и металлургическая задача. Решение металлургической задачи основано на модели Леблонда. Данная модель описывает процесс металлургического превращения одной фазы в другую. Процесс зависит от времени фазового превращения и скорости охлаждения или нагрева материала. Модель подходит для описания любого диффузионного металлургического процесса:

,

где t(T) — функция времени превращения одной фазы в другую в зависимости от температуры; F(Vохл) — функция скорости охлаждения/нагрева; Peq — доля исчезающей фазы; P — доля появляющейся фазы; Т — температура среды, С°.

В нашей задаче есть три металлургических фазы. В зависимости от скорости охлаждения/нагрева возможно шесть металлургических процессов, которым соответствуют шесть моделей Леблонда. Мы считаем фазовые процессы в данной задаче обратимыми, поэтому ограничиваемся тремя моделями Леблонда.

Модели представлены в виде графиков на рис. 9.

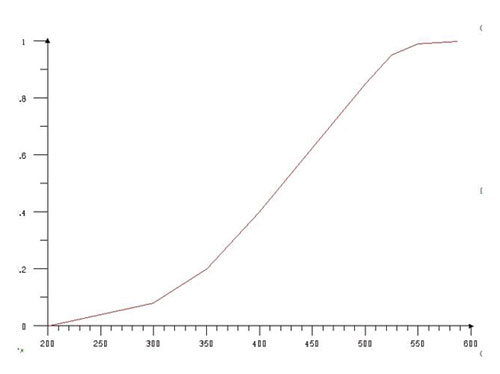
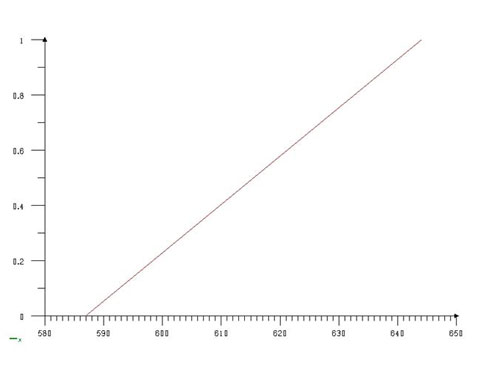
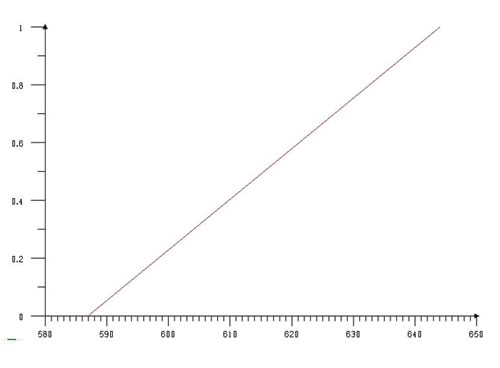
Рис. 9. Графики трансформаций: а — 1-й фазы во 2-ю; б — 1-й фазы в 3-ю; в — 2-й фазы в 3-ю

На рис. 10 показана схема решения металлургической задачи при охлаждении.

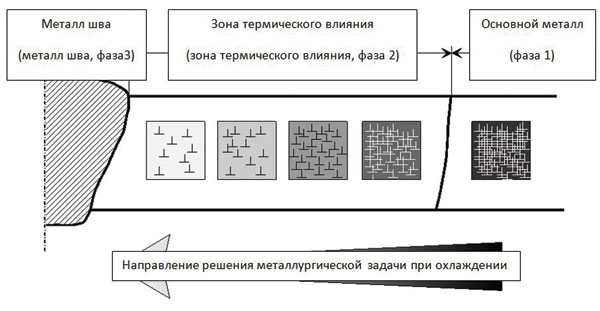
Рис. 10. Схема решения металлургической задачи

В результате расчетов мы получаем поля распределения металлургических фаз (рис. 11).

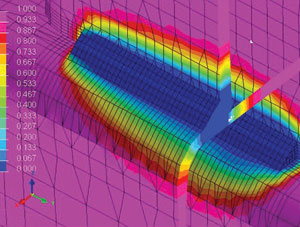
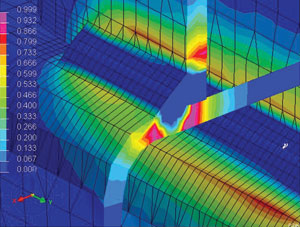
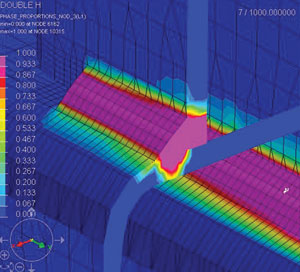
Рис. 11. Результаты металлургической задачи: а — поля распределения фазы 3 после сварки; б — поля распределения фазы 2 после сварки; в — поля распределения фазы 1

Теперь, когда тепловая и металлургическая задачи решены, приступаем к решению задачи механики. Решение этой задачи сводится к определению термических деформаций. Для этого требуется задать: модуль упругости первого рода, коэффициент Пуассона, коэффициент теплового расширения, а также кривые упрочнения для металлургических фаз, которые мы описали ранее. Все данные представляются в виде зависимости от температуры: от 0 или 20 °С до температуры плавления материала (рис. 12).

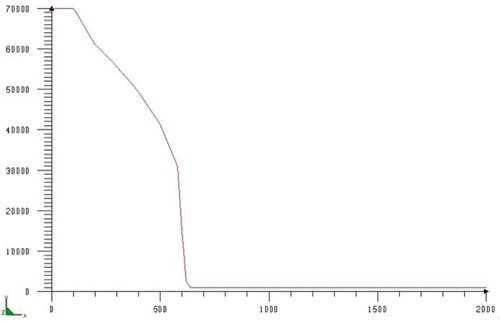
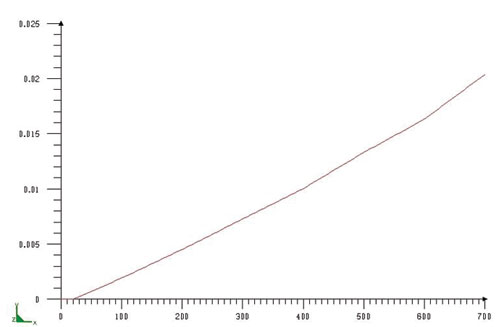
Рис. 12. Результаты металлургической задачи: а — Е — модуль упругости первого рода, Н/мм2; б — L — коэффициент теплового расширения, К-1

Также требуется задать граничные условия. Выбираем три варианта закрепления, которые могут быть реализованы на практике (рис. 13).

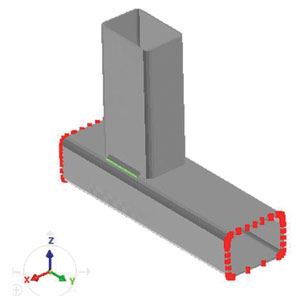
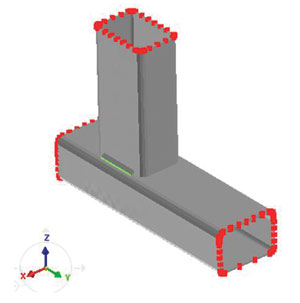
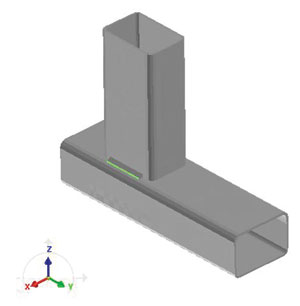
Рис. 13. Граничные условия механической задачи: а — конструкция закреплена с двух сторон; б — конструкция закреплена с трех сторон; в — конструкция не закреплена

Узлы, которые выделены красным цветом, не могут перемещаться по осям координат.

Решая задачу механики, программа использует данные ранее рассчитанных температурных полей и данные решения металлургической задачи. Результаты распределения полей деформаций и изменения деформаций в течение сварки в точке приведены на рис. 14.

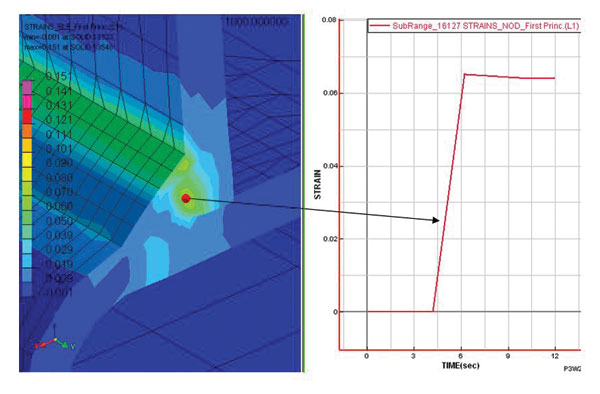
Рис. 14. Термические деформации в точке: а — поля деформаций по первым главным деформациям, мм; б — график зависимости деформаций от времени в точке по первым главным деформациям

Следствием влияния термических деформаций является общее коробление конструкции. Результаты коробления конструкции представлены в трех вариантах (рис. 15-17).

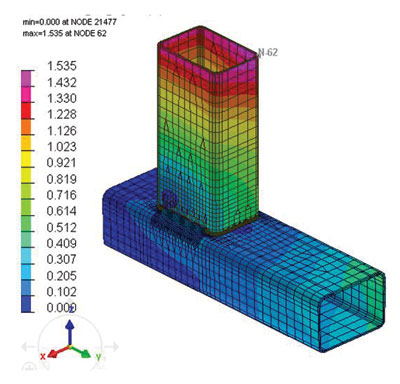
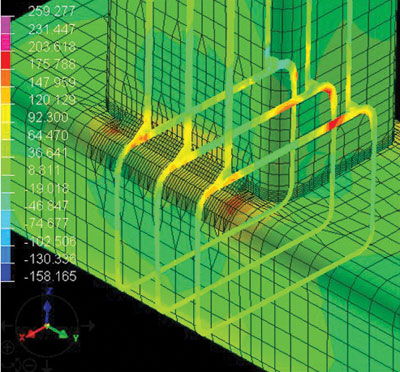
Рис. 15. Распределение деформаций и напряжений по конструкции для варианта 1: а — деформации в случае, когда конструкция закреплена; б — деформации в случае, когда конструкция в свободном состоянии; в — напряжения в сечениях по первой главной площадке напряжения

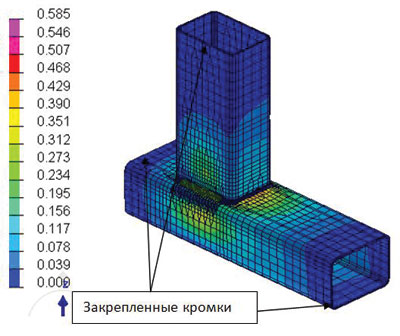
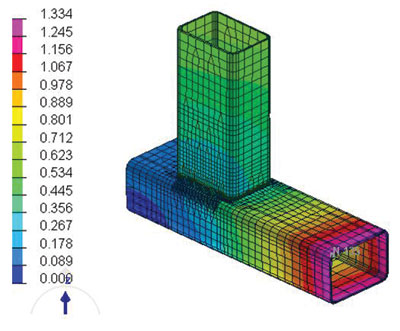
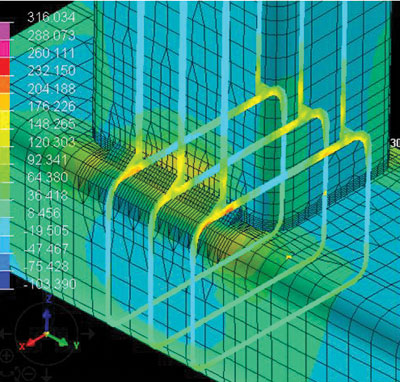
Рис. 16. Распределение деформаций и напряжений по конструкции для варианта 2: а — деформации в случае, когда конструкция закреплена; б — деформации в случае, когда конструкция в свободном состоянии; в — напряжения в сечениях согласно первой главной площадке напряжения

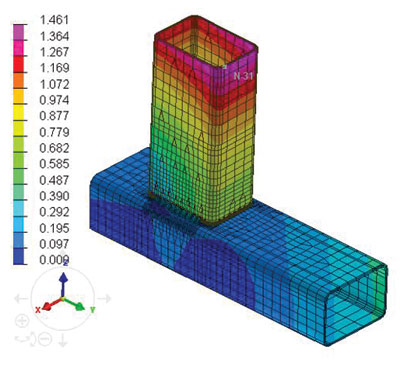
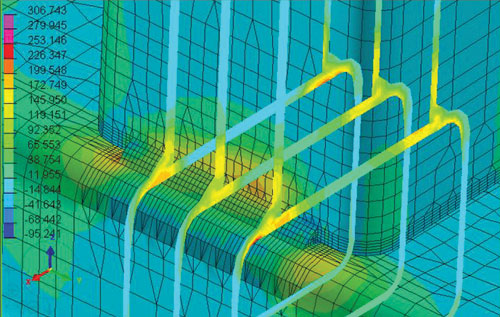
Рис. 17. Распределение деформаций и напряжений по конструкции для варианта 3: а — деформации в случае, когда конструкция в свободном состоянии; б — напряжения в сечениях согласно первой главной площадке напряжения

Анализ результатов расчетов показывает, что минимальное коробление наблюдается в варианте 2 (см. таблицу).

Таким образом, задача оптимизации технологии по выбору условий закрепления с целью снижения коробления решена.

Результаты расчета по трем вариантам

Заключение

Внедрение математического моделирования процессов сварки с помощью SYSWELD позволит значительно сократить затраты на опытное производство, повысить качество выпускаемой продукции, решать сложные технологические задачи, на преодоление которых, как правило, уходит много времени. Численное моделирование процессов сварки поможет сделать продукцию намного более технологичной, поскольку все варианты технологии можно оценить предварительно, до воплощения конструкции в металле. Качественная отработка технологии с помощью SYSWELD обеспечит изделию длительную безаварийную эксплуатацию, что, безусловно, повышает репутацию производителя.

Все это наряду с повышением производительности труда дает производственнику неоспоримые конкурентные преимущества, что очень важно в условиях современного российского рынка.

САПР и графика 1`2011