Конечно-элементный анализ для всех. Часть 3. Получение реальных численных данных для моделирования любого процесса — от землетрясения до запуска ракет
Если вы ознакомились с первыми двумя частями данной статьи, то уже знаете о динамическом поведении конструкций гораздо больше, чем 95% ваших коллег — инженеров и конструкторов. После прочтения статьи о том, как расчет колебаний дает ключевую информацию о прочностных свойствах конструкции (см. «САПР и графика» № 1'2011), термины «собственные частоты», «формы колебаний», «коэффициент участия массы», «энергия деформации» уже прочно вошли в ваш лексикон.
До сих пор разговор фокусировался вокруг качественных составляющих механического поведения конструкций, вызванного динамическим нагружением. В этой последней части статьи мы продемонстрируем, как получить реальные количественные данные (то есть смещение и нагрузки) при помощи обычного анализа собственных частот колебаний.
Расчеты с минимальными временными затратами
Динамическая реакция структуры обусловлена ее собственными формами колебаний. Если вы нанесете по конструкции удар, ее динамическая реакция будет состоять из совокупности индивидуальных колебаний. Мы знаем, что с математической точки зрения каждое колебание имеет свою частоту, форму и некоторую долю массы, приходящуюся на эту форму (коэффициент участия массы). Все эти данные выводятся из базового уравнения движения:
ma+kx = 0.
Из этого уравнения можно вывести стандартное линейное решение уравнения динамики в виде:
ω = √K/m,
где ω — собственная частота колебаний системы. Поскольку в уравнении не используется переменная силы, мы не можем рассчитать реальные показатели смещения и нагрузок.
Для получения реальных данных потребуется ввести параметр силы: ma+kx=F.
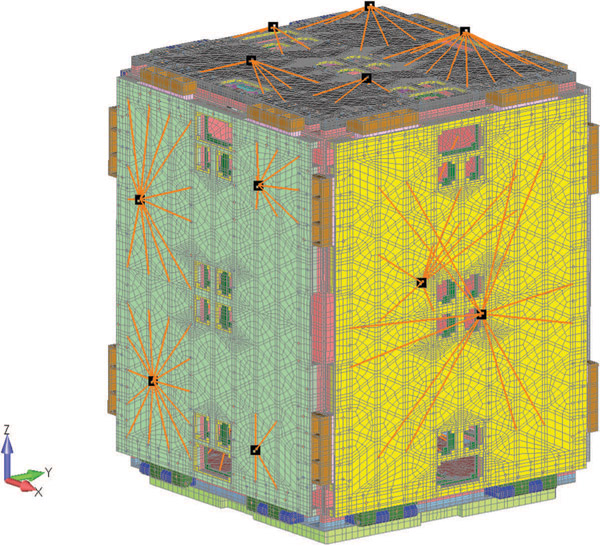
Конечно-элементная модель спутника, на которой изображены точки крепления аппаратуры (черные квадраты), представляющие собой идеальные элементы с массовыми характеристиками в центре тяжести и соединенные жесткими связями с корпусом. В качестве воздействия использована функция спектральной плотности мощности
Грубый подход к решению задачи состоит в расчете модели во временном интервале. В модели задаются смещение, сила, инерционная нагрузка в зависимости от времени, а в результате компьютер выдает несколько тысяч решений. Позже мы будем вынуждены рассмотреть огромное количество выходных данных (не забывайте, что мы проводим полный расчет по каждому временному отрезку), для того чтобы понять, что, где и когда пошло не так. Это может оказаться очень сложной, а порой и практически бесполезной задачей.
Задав нагружение в зависимости от частоты (смещение, сила или ускорение как функции от частоты), можно получить массу возможностей для самых разных стратегий решения, очень эффективных в численном отношении. Сначала вы проводите анализ свободных колебаний, а затем прикладываете нагрузку, зависящую от частоты. Линейный расчет в этом случае производится только по каждому типу свободных колебаний. Результирующие смещения и нагрузки могут рассматриваться индивидуально или совокупно — так, чтобы отразить общую реакцию системы на воздействия, вызванные нагружением. Данная технология очень эффективна, поскольку позволяет сократить количество решений с нескольких тысяч до единиц. И хотя данный вариант подходит не для всех типов конструкций (только для линейных), в тех случаях, когда вы сможете им воспользоваться, вы получите возможность быстро собрать все необходимые данные для понимания динамических характеристик изделия с минимальными временными затратами (потратив несколько минут, а не дней).
Разложение по частотам
Вибрационные нагрузки встречаются гораздо чаще, чем может показаться. В предыдущей части статьи мы рассматривали весьма простой пример вибрационного конвейера. Теперь давайте разберем более сложную конструкцию.
На рис. 1 показана высокоточная зеркальная оптическая система, используемая в конструкции самолетов или вертолетов. Воздухоплавательные конструкции создают насыщенную вибрациями среду за счет работы своих высокоскоростных турбореактивных двигателей, поворотных лопастей и т.п. Для оценки надежности конструкции можно провести виртуальный динамический эксперимент. В качестве цели нам требуется получить данные о деформациях при динамическом нагружении в фокусной точке зеркала под воздействием сильной вибрации.
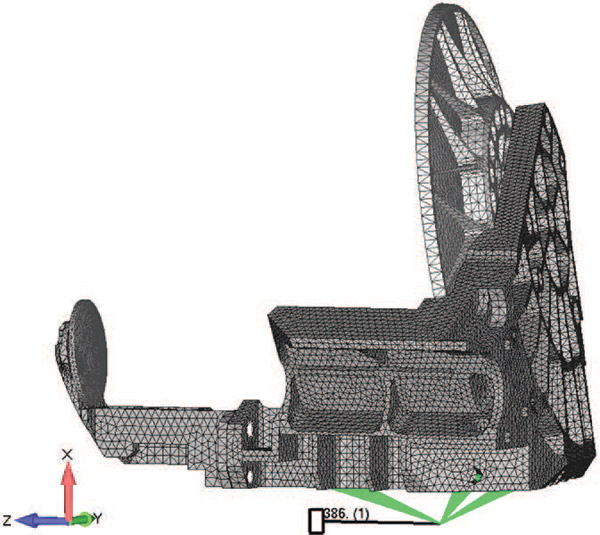
Рис. 1. Изображение усовершенствованной оптической установки для воздухоплавательных систем, размещенной на виртуальном вибростенде
Не изготавливая физический прототип зеркала, можно приложить к модели синусоидальную развертку ускорения от 200 Гц до 3 кГц и посмотреть, какие изменения они вызовут в конструкции. На рис. 2а и б изображены результирующие графики ускорения и смещения как функции частоты для синусоидальной развертки.
Система зеркал имеет собственные частоты 710, 1292, 1570, 1996 Гц и т.д. Но, как видно из рис. 2а и б, только колебание на частоте 710 Гц вызывает действительно значимые индуцированные ускорения и смещения. Это объясняется тем, что данная форма колебаний совпадает с силовой функцией и коэффициент участия массы в ней равен 35 % в направлении силовой функции. В принципе, мы предвидели результат еще до проведения анализа, но теперь получили точные цифры.
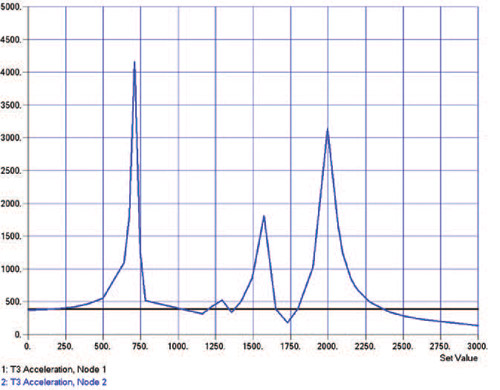
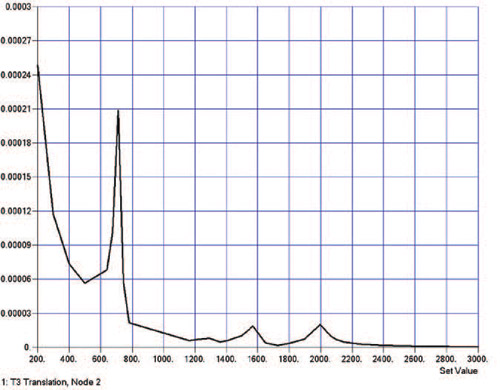
Рис. 2. Полученные в результате виртуального моделирования воздействия вибрации значения ускорения и смещения фокуса крупного зеркала, устанавливаемого на летательном аппарате. Ускорение показано в сантиметрах в секунду по оси y (а), а смещение — в сантиметрах по оси y (б)
Анализ спектральной плотности мощности (СПМ)
Производство спутников — дорогостоящий процесс, ошибки в нем оказываются еще более дорогостоящими. Во время запуска (рис. 3) они подвергаются воздействию широкого спектра хаотических вибраций (ускорений) от ракетного двигателя, отделения ступеней, акустического шума и т.п. Ни одна из частот воздействия не преобладает над остальными, имеет место множество наслоений шумовых явлений, происходящих хаотично.

Рис. 3. Запуск ракеты и прочие хаотические явления создают спектры вибрации (ускорения), которые лучше всего моделировать статистическим методом при помощи функций спектральной плотности мощности
Для числового моделирования подобной нагрузки применяется статистический подход, при котором результаты измерения ускорения переводятся в функцию спектральной плотности мощности (СПМ), где единицы ускорения сбалансированы по частоте (рис. 4). Мы снова получили кривую нагружения, в которой приложенная нагрузка зависит от частоты.
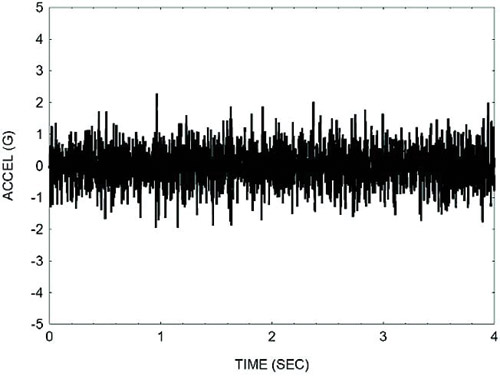
Рис. 4. Значения ускорений ракеты преобразованы в функции спектральной мощности, единицы ускорения возведены в квадрат. Прикладываемая нагрузка зависит от частоты
Перед тем как начинать считать…
|
Статистическая сущность данных расчетов состоит в переводе данных об общем времени действия ускорений в функцию спектральной плотности мощности (СПМ). Амплитуды СПМ по сути являются среднеквадратичными действующими значениями ускорения, которые соответствуют нормальному статистическому распределению, где среднее значение равно нулю, а на графике отображается среднеквадратичное отклонение в зависимости от частоты. Звучит парадоксально, но это весьма эффективный способ преобразовать хаотические случайные шумовые явления в удобную для расчетов функцию нагружения.
Еще один уникальный аспект СПМ-анализа: предполагается, что все собственные формы конструкции колеблются и приводятся в возбужденное состояние функцией СПМ одновременно. По аналогии с колокольным звоном результирующий отклик является совокупностью диапазонов всех частот структуры в интересующих исследователя рамках.
Например, конечно-элементная модель спутника включает элементы полезной нагрузки, смоделированные в виде элементов сосредоточенных масс. Эти полезные нагрузки прикрепляются к корпусу модели посредством жестких связей. Зачастую задачей анализа СПМ становится определение передаточной функции конструкции, то есть того, как нагрузки при ускорении будут передаваться через каркас спутника на контрольно-измерительные приборы.
Итоговая передаточная функция — это не что иное, как еще одна спектральная плотность мощности. Получив ее, мы задействуем этот результат для дальнейшего, более подробного СПМ-анализа контрольно-измерительных приборов, чтобы понять, выдержат ли они запуск спутника.
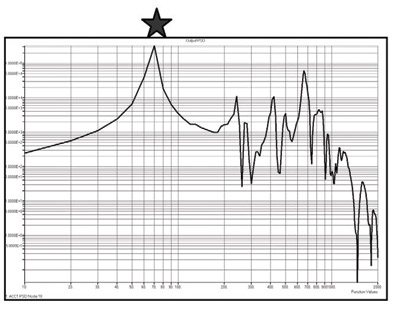
Рис. 5. Итоговый график анализа спектральной плотности спутника указывает расположение первой формы собственных колебаний (отмечено звездочкой) на уровне 70 Гц. На графике частота откладывается по оси x, спектральная плотность мощности g,
равная 2/Гц, — по оси y
Преобладающая частота колебаний спутника — около 70 Гц (рис. 5); на графике результирующей функции спектральной плотности мощности это отражено в виде резкого скачка вверх на этой частоте (отмечено звездочкой). Зная, что наши контрольно-измерительные приборы подвергнутся воздействию частот в 70 Гц, мы изменили бы конструкцию таким образом, чтобы каркас спутника стал жестче, а преобладающая частота его собственных колебаний не равнялась 70 Гц. Однако даже без анализа спектральной плотности мощности четкое представление о частотах собственных колебаний, их формах и соответствующих им коэффициентах участия массы позволяет вам делать надежные прогнозы.
Итак, теперь вы владеете основными понятиями, терминологией и общей схемой работы в сфере линейной динамики. Обычный анализ форм колебаний может стать отличным стартом для успешного решения ваших задач проектирования. Почему бы не попробовать?
![]()
Copyright © by Level 5 Communications, Inc., 1283 Main St., Dublin, NH 03444, All Rights Reserved. www.deskeng.com


