Расчет аэродинамических характеристик крыла с использованием программного комплекса ANSYS CFX

Валерий Вождаев

Создание летательного аппарата нового поколения невозможно без анализа его аэродинамических характеристик еще на ранних стадиях проектирования. От глубины исследования формы несущих поверхностей и обводов планера напрямую зависят летно­технические характеристики разрабатываемого самолета. Развитие теоретических основ численных методик расчета аэродинамических характеристик летательных аппаратов можно разделить на несколько этапов:

• линейная теория (60­е годы);
• нелинейная теория полного потенциала скорости (70­е годы);
• уравнения Эйлера (80­е годы);
• уравнения Навье — Стокса, осредненные по Рейнольдсу (90­е годы).

Физику процесса обтекания тела произвольной формы потоком газа наилучшим образом отражают методики, основанные на решениях уравнений Навье — Стокса. С появлением программных средств, базирующихся на численных решениях уравнений Навье — Стокса, стало возможно получить расчетным путем ряд важных аэродинамических характеристик самолета, в частности вычислить максимальное значение коэффициента подъемной силы Cy max. При расчетах аэродинамических характеристик объектов сложной пространственной конфигурации с использованием такого подхода требуются большие объемы оперативной памяти компьютера, поскольку допустимые размеры расчетной сетки пропорциональны объему оперативной памяти компьютера. Рост возможностей вычислительной техники, наблюдаемый в последние годы, позволяет применять программы, основанные на численных решениях уравнений Навье — Стокса, для расчета характеристик обтекания таких объектов, как самолет. Одной из популярных коммерческих программ в этой области является ANSYS CFX (лицензия ЦАГИ № 501024).

Использование CFX в области авиастроения является рациональным, поскольку пакет ANSYS, помимо аэродинамического модуля CFX, содержит ряд других вычислительных модулей (STRUCTURAL, FATIQUE и д.р.), что обеспечивает возможность совместного решения задач аэродинамики, аэроупругости и прочности.

Рассмотрим особенности расчета обтекания прямого крыла бесконечного размаха с профилем GA(W)­1. Этот профиль был создан известным американским аэродинамиком Уиткомбом для применения на дозвуковых скоростях полета.

Комплекс ANSYS оснащен встроенными интерфейсами ряда основных CAD­программ. Геометрическая модель, созданная в программе трехмерного графического моделирования, считывается любой из программ комплекса. Твердотельная геометрическая модель отсека крыла, сохраненная в формате Parasolid, была импортирована в профессиональный сеточный генератор ANSYS ICEM, где методом Octree была построена неструктурированная расчетная сетка, состоящая из 3 млн объемных тетраэдрических элементов (рис. 1). Вблизи поверхности крыла параметры Tetra Size Ratio и Height Ratio были равны 1.2. Максимальный размер элементов на передней кромке крыла составил 1 мм. Для обеспечения нужной точности решения и сходимости расчета элементы расчетной сетки имели Aspect Ratio более 0.3 и Min Angle более 20°. Кроме того, необходимо, чтобы габаритные размеры расчетной области многократно превышали характерный размер исследуемого объекта. В данном случае использовалась прямоугольная расчетная область длиной 35 и высотой 30 м. Размах крыла равен 4 м, а хорда крыла — 3,3 м. Моделирование крыла бесконечного размаха осуществлялось путем задания в препроцессоре CFX­PRE справа и слева от крыла граничных условий типа Symmetry. Типы граничных условий, используемых в данной задаче, показаны на рис. 2.

Рис. 1. Фрагмент расчетной области

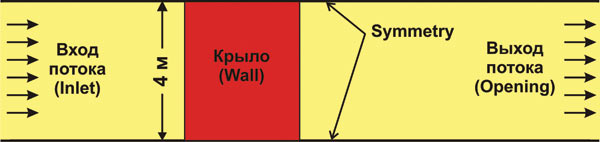
Рис. 2. Схема обтекания отсека крыла при виде сверху

В пристеночных областях при построении расчетной сетки для наилучшего моделирования пограничного слоя образованы слои призматических элементов (см. рис. 1). При решении задачи обтекания крыла (где одной из расчетных величин является касательное напряжение) очень важно контролировать величину Y+. Значение Y+ характеризует относительную высоту первой ячейки пограничного слоя, которая задается в ICEM при построении призматических элементов. После окончания вычислений в среде постпроцессора CFX­POST можно визуализировать Y+ на расчетной модели (рис. 3).

Рис. 3. Распределение Y+ на модели крыла

При использовании методик, основанных на численных решениях уравнений Навье — Стокса, качество полученного результата во многом зависит от выбора модели турбулентности. В программном комплексе ANSYS CFX реализовано достаточно большое число моделей турбулентности. Однако ни одна из них не является универсальной для всех существующих классов задач. Из многообразия моделей турбулентности, используемых при расчетах аэродинамических характеристик, можно выделить известные модели турбулентности k-ε и k-ω. Они являются двупараметрическими моделями турбулентности, которые базируются на рассмотрении кинетической энергии турбулентных пульсаций k. В качестве второго уравнения применяют уравнение либо переноса скорости диссипации турбулентной энергии ε, либо удельной скорости диссипации энергии ω. Модель переноса касательных напряжений SST (двухслойная модель Ментера) использует модель k-ω в пристеночной области и преобразованную модель k-ε вдали от стенки. В новые версии программы CFX включен бета­вариант модели турбулентности Spalart­Allmaras (S­A). Эта модель является однопараметрической, использующей одно дифференциальное уравнение переноса.

Расчеты с применением программного комплекса ANSYS CFX проводились на сервере с 8­ядерным процессором Intel Xeon 2,83 ГГц и 16 Гбайт ОЗУ. Для получения стационарного решения в зависимости от типа модели турбулентности и угла атаки крыла потребовалось осуществить 40­60 итераций.

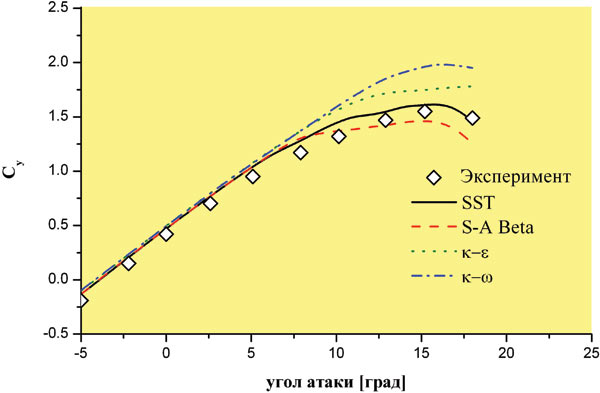
Рис. 4. Зависимость коэффициента подъемной силы от угла атаки

Вычисления проводились при числе Маха 0,2 и числе Рейнольдса 2,2Ѕ106. В препроцессоре ANSYS CFX отсутствует возможность напрямую задавать число Рейнольдса. В связи с этим число Рейнольдса вычислялось в CFX­PRE по величине статического давления, соответствующего определенному коэффициенту кинематической вязкости.

В результате проведенных расчетов были получены величины сил и моментов, действующих на отсек крыла на заданных углах атаки. Зависимость коэффициента подъемной силы Сy от угла атаки сравнивалась с аналогичными экспериментальными данными, полученными американскими специалистами NASA Венцем и Ситхарамом (SAE Paper 740365). На линейном участке все рассмотренные модели турбулентности продемонстрировали удовлетворительное совпадение расчетных и экспериментальных данных. В зоне Сy max максимальное соответствие с экспериментальными данными показала модель турбулентности SST (рис. 4). С использованием постпроцессора CFX­POST файл с результатами расчета позволяет визуализировать картину обтекания крыла. Линии тока и поле скоростей хорошо иллюстрируют отрывное течение, соответствующее углу атаки, при котором достигается Cy max крыла (рис. 5).

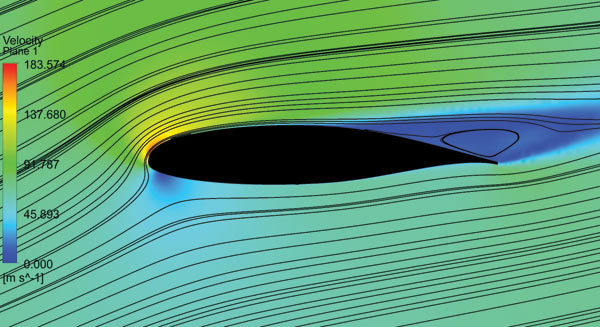
Рис. 5. Визуализация обтекания отсека крыла

Таким образом, в результате выполненной работы показано, что при расчетах характеристик обтекания аэродинамических поверхностей использование модели турбулентности SST приводит к более высокому результату. 

САПР и графика 2`2011