Использование САПР для решения прикладных задач
При проектировании современных технологий наиболее эффективным инструментом, позволяющим существенно сэкономить энергетические и интеллектуальные ресурсы, служат различные виды моделирования: математическое, аналоговое, физическое, компьютерное, графическое (рис. 1).
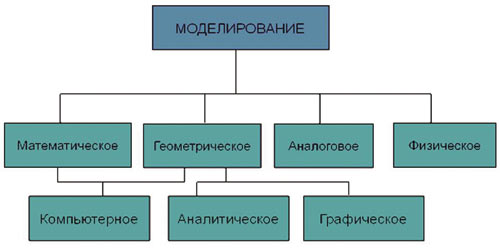
Рис. 1. Классификация видов моделирования
Иногда трудно отделить один вид моделирования от другого. Так, аналоговое моделирование можно считать разновидностью физического моделирования, а компьютерное моделирование базируется на математических моделях процессов или объектов. В то же время геометрическое моделирование является, строго говоря, частью математического моделирования, но вместе с тем может рассматриваться как самостоятельный вид, поскольку использует мощный аппарат аналитической, дифференциальной и графической (то есть начертательной) геометрии. Такое разделение геометрии весьма условно и сложилось исторически, в ходе развития математики и приложения ее к решению практических задач. Тенденции современного научнотехнического прогресса требуют интеграции отдельных наук, в частности объединения геометрии в единую область знаний, что приводит к необходимости учета этого требования в учебных программах технических вузов.
В последнее время действенным средством решения множества прикладных задач становится графическое компьютерное моделирование, что связано с совершенствованием CAD/САМсистем и графических пакетов программ, а также повышением возможностей компьютерной техники.
Некоторые из них допускают использование «поверхностных» аналогий, когда распределение какоголибо параметра по площади (или объему) тела представляется в виде поверхности некоторой пространственной эпюры. При моделировании реальных процессов такие поверхности представляют собой весьма сложные геометрические объекты, изображение которых на плоскости сопряжено с существенными затруднениями. Вместе с тем задача зачастую состоит не только в том, чтобы показать контуры подобной поверхности, но и, что гораздо важнее, построить линию пересечения ее отдельных участков.
В процессах обработки давлением тонкого слоя металла пространственную эпюру контактных давлений можно моделировать предельной песчаной насыпью, образованной на пластине, сходной по форме с контуром заготовки. Очевидно, что такая насыпь является поверхностью одинакового ската. Поскольку любой многосвязный контур с достаточной степенью точности можно аппроксимировать отрезками прямых и дугами окружностей, можно считать, что указанная поверхность состоит из плоских и конических участков. Линии их пересечения образуют ребра (так называемые гребни).
Проекции этих ребер на плоскость контакта инструмента и заготовки дают возможность решать некоторые задачи пластического формоизменения материала, а именно:
- фронтальная и профильная проекции позволяют определять объем эпюры контактных давлений, а значит, и силы, необходимые для деформирования слоя металла;
- горизонтальная проекция представляет собой линию раздела течения металла (ЛРТМ), которая характеризует распределение потоков металла на контактной поверхности. Очевидно, что ЛРТМ представляет собой эквидистанту, то есть геометрическое место точек, равноудаленных от контура заготовки.
Следовательно, решая графическими методами задачу о построении линии пересечения поверхностей многогранников и тел вращения, можно определить некоторые параметры процессов обработки металлов давлением.
Для управления потоками металла по полотну поковки в процессах обработки давлением используют технологические вырезы или технологические выемки, которые позволяют предотвращать ряд дефектов («прострел», неудовлетворительная завязка волокон, «утяжина»), а также регулировать распределение объемов металла по площади заготовки. Обычно такие вырезы (выемки) выполняются в форме круга. В этом случае всё многообразие построений пространственной эпюры контактных давлений (ПЭКД) можно свести в основном к трем чисто геометрическим задачам.
1. Пересечение пирамиды и конуса
Пусть деформированию между жесткими плитами подвергается квадратная пластина с круглым вырезом (рис. 2а).
В соответствии с вышеприведенными рассуждениями задача сводится к построению проекций линии пересечения поверхности многогранника (пирамиды) и кругового конуса (рис. 2б). Рассмотрим случай, когда оси обеих поверхностей совпадают. Тогда точка 8 является точкой пересечения образующих (рис. 2в). Конус при этом перевернутый, то есть его вершина расположена ниже основания.
Для решения поставленной задачи должны быть заданы контур пластины, который определяется ее размерами, и угол наклона образующей (линии ската) к горизонтальной плоскости, который зависит от физических характеристик материала пластины.
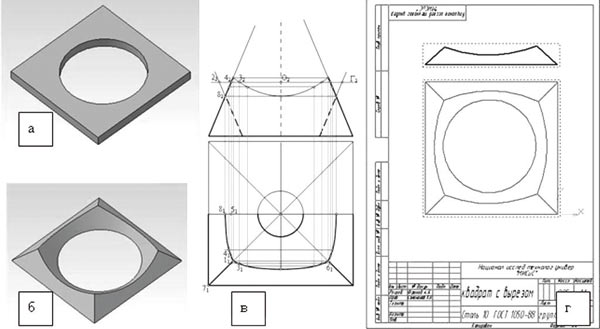
Рис. 2. Построение линии пересечения пирамиды и конуса
Последовательность графических построений эпюры, выполненных вручную с использованием способа вспомогательных секущих плоскостей, вполне очевидна. Кривые линии пересечения конуса и пирамиды являются отрезками параболы, поскольку грани пирамиды наклонены к основанию под тем же углом, что и образующие конуса, то есть параллельны друг другу. Горизонтальная проекция линии пересечения в силу свойств поверхности одинакового ската представляет собой эквидистанту, расстояния от которой до точек контура попарно равны, в чем легко убедиться на рис. 2в.
Для моделирования поверхностей одинакового ската весьма удобен графический пакет КОМПАС3D, который позволяет сначала создавать 3Dмодели пространственных объектов (рис. 2б), а затем получать по ним чертежи в проекционном виде (рис. 2г). Из сравнения изображений в и г на рис. 2 очевидно их почти полное совпадение. Удобство КОМПАСа для решения подобных задач заключается в том, что выдавливание поверхностей в нем производится под одинаковым углом к основанию, что и требуется для создания поверхностей одинакового ската. Разумеется, компьютерное решение, даже с учетом построения твердотельной модели, гораздо быстрее «ручного».
Следует заметить, что в общем случае, когда в основании лежит какойлибо многоугольник, поверхность одинакового ската представляет собой многогранник довольно сложной конфигурации, что усложняет как автоматизированное, так и «ручное» решение задачи.
2. Пересечение двух конусов и «крыши»
Пусть деформированию между жесткими плитами подвергается прямоугольная пластина с двумя круглыми вырезами разного радиуса.
В данной задаче, где внутренний контур состоит из двух окружностей, нас интересует лишь частный вопрос построения линии пересечения двух перевернутых конусов и определения формы этой линии, поскольку задача о пересечении конуса плоскостью нами решена ранее.
Очевидно, что кривая, равноудаленная от двух окружностей, не что иное, как гипербола, так как представляет собой проекцию линии пересечения двух конусов, что и подтверждает рис. 3.
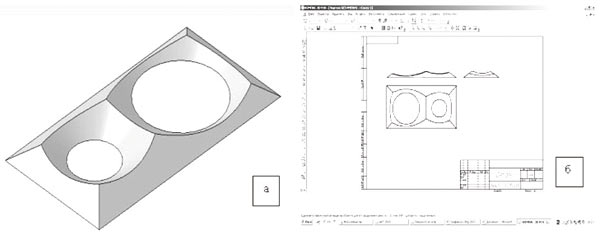
Рис. 3. Прямоугольная пластина с двумя вырезами: а — твердотельная модель ПЭКД; б — проекционный чертеж ПЭКД
3. Пересечение двух разнонаправленных конусов
Пусть деформированию между жесткими плитами подвергается круглая пластина с круглым нецентральным вырезом.
Задача сводится к построению линии пересечения двух конусов, один из которых является перевернутым (рис. 4). Анализ формы линии пересечения двух разнонаправленных конусов позволяет сделать вывод, что это эллипс. Проекция эллипса на горизонтальную плоскость также представляет собой эллипс.
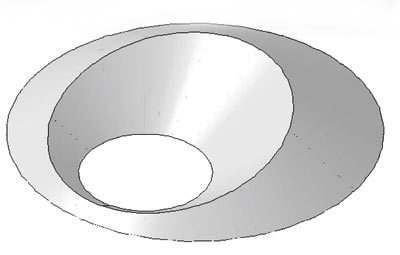
Рис. 4. Поверхность одинакового ската для круглой пластины с вырезом
В случае если центр выреза расположен за пределами контура пластины, то есть вырез представляет собой не полный круг, а усеченный, решение принципиально не отличается от предыдущего, разница лишь в том, что ребро является дугой эллипса. При этом указанное ребро упирается в основание конуса в точках границы выреза.
Другие случаи пересечения поверхностей одинакового ската, не рассмотренные здесь, составляют лишь комбинации представленных построений.
Таким образом, с помощью КОМПАСа можно получить решение для сложных контуров и поверхностей (рис. 5а). Однако это удается не всегда. Для целого класса контуров выдавить поверхность до конца, то есть получить предельную насыпь, невозможно. Например, нельзя построить (выдавить) поверхность одинакового ската для сравнительно простого контура, изображенного на рис. 5б.
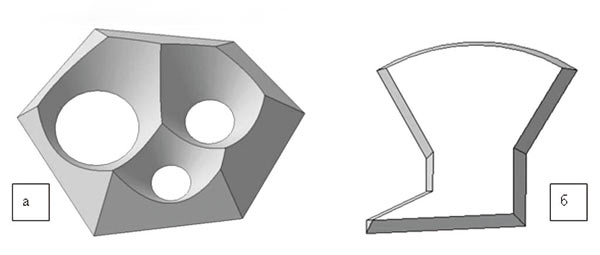
Рис. 5. Возможности моделирования поверхностей одинакового ската
В тех случаях, когда какаялибо САПР не в состоянии решить поставленную задачу, целесообразно использование универсальных пакетов программ либо специализированных для узкого круга задач. Таким специализированным программным комплексом можно считать PARSHTAMP, разработанный для моделирования процессов объемной штамповки и ковки и позволяющий строить ЛРТМ для весьма сложных контуров. Чтобы сравнить результаты компьютерного моделирования в обоих пакетах, рассмотрим относительно простую задачу о протяжке полосы в процессе ковки. Нас интересует, как будет выглядеть ПЭКД, моделируемая поверхностью одинакового ската в той части заготовки, которая подвержена деформированию. Очевидно, что она представляет собой «крышу» (рис. 6а). Из технологических соображений для уменьшения силы, необходимой для осадки заготовки, и выпучивания сторон поковки целесообразно применение технологической выемки. Тогда ПЭКД значительно уменьшится в размерах (рис. 6б) и течение металла в сторону края заготовки несколько выровняется, о чем свидетельствует картина течения металла, соответствующая расположению ЛРТМ в плоскости контакта инструмента и заготовки (рис. 6в). Аналогичные результаты получены с помощью PARSHTAMP (рис. 6ге). При этом программный комплекс PARSHTAMP позволяет путем варьирования размеров и положения технологической выемки получать различные варианты картины течения. Сравнение моделей в и е на рис. 6 доказывает хорошее совпадение результатов построений в представленных САПР.
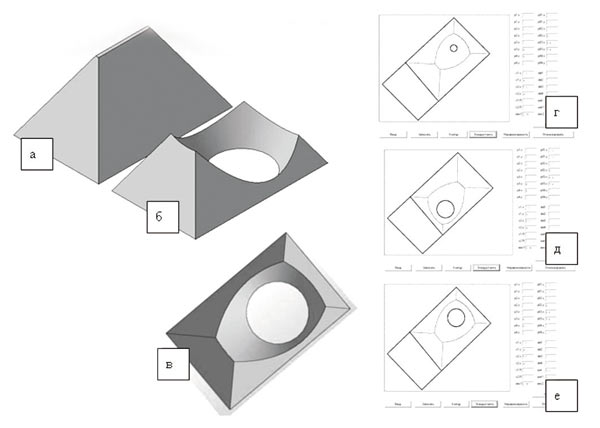
Рис. 6. Комплексное моделирование прикладных задач
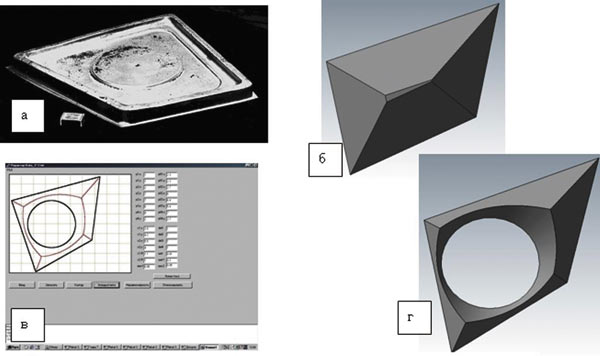
Рис. 7. Пример промышленного использования САПР
Внедрение компьютерных разработок в промышленность оказывает помощь при решении практических задач. Так, при подготовке на одном из российских заводов серийного производства поковки (рис. 7а) возник ряд трудностей: оказалось, что мощностей оборудования не хватает для штамповки изделия и она оформляется неравномерно. Анализ картины течения металла, произведенный с помощью компьютерного моделирования (рис. 7б), подтвердил результаты промышленного эксперимента, а также позволил предложить рациональный вариант решения поставленной задачи. Для улучшения макроструктуры подреберных зон и обеспечения полного формирования поковки в плоской заготовке до начала штамповки на основе результатов виртуального эксперимента (рис. 7в, г) было выполнено круглое отверстие. Это позволило отштамповать поковку в соответствии с требованиями заказчика. При этом не пришлось переделывать дорогостоящий инструмент изза изменения технологии производства, а также передавать заказ на сторону ввиду отсутствия мощного оборудования.
Таким образом, активное применение графических методов и CAD/CAMсистем для решения прикладных задач позволяет получать хорошие результаты.


