Спиральные, спиральные составные и спиралевидные (квазиспиральные) компенсаторы трубопроводов

Виктор Чебыкин (Инженер-конструктор, ЗАО «Строительно-монтажная лаборатория» (Новосибирск))

Спиральные компенсаторы

Спиральные составные компенсаторы

Спиралевидные (квазиспиральные) компенсаторы

Выводы

Библиографический список

Пружина — деталь машины или механизма, служащая для временного накопления энергии под влиянием нагрузки за счет упругой деформации и, по прекращении действия нагрузки, восстанавливающая свою первоначальную форму, отдавая накопленную энергию. Пружины широко применяются в технике для поглощения энергии удара и смягчения его действия, виброизоляции и т.д. [1].

Отличные упругие свойства винтовых спиральных пружин, простота изготовления и долговечность позволяют применять их в качестве упругих элементов различных устройств, например в подвесках автомобилей.

Спиральные компенсаторы

Можно ли использовать упругие свойства винтовой спиральной пружины в конструкции трубопровода (например, выполнив температурный компенсатор в виде винтовой спиральной пружины)?

3D­моделирование спиральных компенсаторов, расчеты и построения разверток их элементов проводились в конструкторской программе КОМПАС­3D.

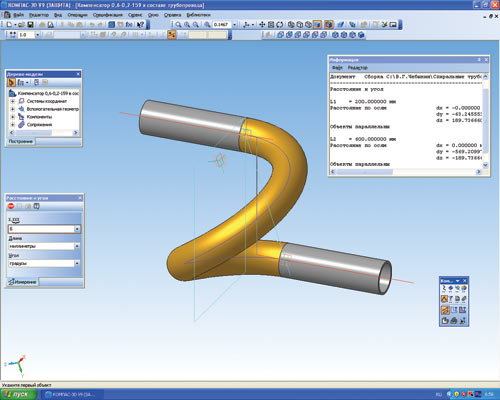
На рис. 1 показана 3D­модель такого компенсатора, имеющего одновитковую спиральную траекторию и соединяющего два параллельных ствола трубопровода. Оси стволов при этом касательны к спирали в точках соединения. С большой долей уверенности можно утверждать, что этот компенсатор более эффективен по упругим свойствам, способности гасить гидравлические удары, компенсировать температурные изменения длины трубопровода, чем, например, П­образный (Г­образный). В связи с равномерным распределением нагрузки по длине спирального компенсатора ресурс его работы будет больше по сравнению с ресурсом П­образного компенсатора.

Расчет траектории спирального компенсатора сводится к определению диаметра спирали, если известны межосевое расстояние между стволами трубопровода и расстояние между торцами стволов.

Диаметр спирали компенсатора определялся по формуле:

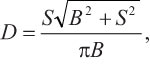 (1)

где D — диаметр спирали компенсатора; S — межосевое расстояние между стволами трубопровода; B — расстояние между соединяемыми торцами стволов.

Трансформируя формулу, можно получить формулы для вычисления B и S для заданного значения D:

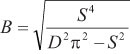 (2)

и

 .(3)

Как видно на информационной таблице измерений рис. 1, точность расчета и построения 3D­модели компенсатора может быть очень высокой: на примере показанного компенсатора погрешность не превышает 1 нм.

Рис. 1. Спиральный компенсатор в составе трубопровода. Экранный снимок

Для создания 3D­модели спирального компенсатора в Дереве модели выбираем плоскость основания спирали, на Компактной панели нажимаем кнопку Спираль цилиндрическая, на Панели свойств указываем число витков — 1;
шаг t, определяемый по формуле:

 , (4)

и диаметр, определенный по формуле (1); нажимаем кнопку Создать объект. Спираль отрисовывается в поле модели. Далее, используя вкладку Вспомогательная геометрия, создаем плоскость, перпендикулярную траектории спирали в одной из ее конечных точек, на ней располагаем эскиз сечения трубы нужного размера и Кинематической операцией создаем 3D­модель компенсатора (термины, выделенные курсивом, здесь и далее — из программы КОМПАС­3D).

Для соединения двух соосных между собой стволов трубопровода компенсатор должен состоять как минимум из двух витков с противоположным направлением завивки спирали (рисунок не показан).

Способов изготовления спиральных компенсаторов может быть несколько: навивка труб в холодном или горячем состоянии с заданными диаметром и шагом; протягивание труб через специальные фильеры и т.п.

Спиральные составные компенсаторы

В статьях [2] и [3] описан метод расчета и трехмерного моделирования витка спирального составного трубопровода, который заключается, в частности, в расчете радиуса расположения вершин Ломаной спирали Rв и определении координат Xi; Yi; Zi вершин. В отличие от расчета витка спирального составного трубопровода, для построения модели спирального составного компенсатора потребуется дополнительно рассчитать (а не задать, как исходный параметр) высоту спирали H:

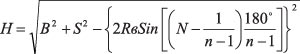, (5)

расшифровка параметров приведена далее по тексту.

Кроме того, отличием спирального составного компенсатора от витка спирального составного трубопровода, описанного в статьях [2] и [3], является наличие двух концевых элементов, имеющих геометрию, отличную от геометрии типовых (промежуточных) элементов. Различие также состоит в том, что внешние грани концевых элементов имеют круглую форму, а оси этих элементов параллельны.

Характерной особенностью такого спирального компенсатора является следующая закономерность — каждому сочетанию исходных параметров:

B — расстояние между торцевыми плоскостями стволов трубопровода;

S — расстояние между осями стволов трубопровода;

n — количество элементов компенсатора;

N — число витков компенсатора

соответствует только одно сочетание полученных данных:

Rв — радиус расположения вершин Ломаной спирали;

H — высота спирали;

М — суммарная длина Ломаной спирали.

Поэтому использование произвольного радиуса Rв для определения координат Xi, Yi, Zi Ломаной не позволит получить траекторию спирали компенсатора, необходимую для соединения стволов трубопровода с заданными параметрами их расположения.

Число витков спирали компенсатора N выбираем из следующего ряда:

 и т.д.,

где n — суммарное количество элементов компенсатора. 

После определения координат вершин составляем таблицу Ломаной и создаем трехмерную модель спирального составного компенсатора. Пример такого компенсатора в составе трубопровода показан на рис. 2.

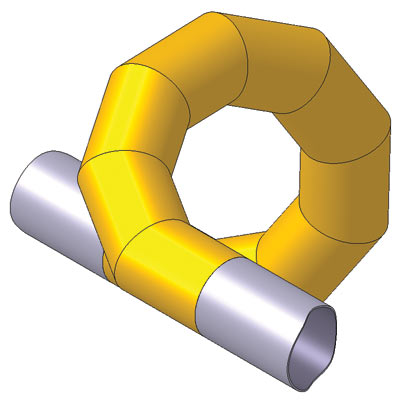
Рис. 2. Спиральный составной компенсатор в составе трубопровода

Используя полученную модель компенсатора, применяя метод веерных сечений его элементов, выполняем построение разверток типового (промежуточного) и концевого элементов. Для получения разверток можно использовать функцию КОМПАС­3D — Листовое тело. С подробным описанием расчета и построения развертки типового элемента с вариантами выполнения можно ознакомиться в статье [3].

По полученным разверткам производят раскрой листовых или трубных заготовок, после чего собирают компенсатор. Развертки листовых и трубных заготовок должны иметь различие в геометрии, если они строятся с учетом толщины материала. Статья [4] посвящена учету толщины материала при расчете разверток соединяемых патрубков.

На рис. 3 показаны спиральные составные компенсаторы, имеющие разное количество витков и элементов и предназначенные для соединения одной и той же пары стволов трубопровода.

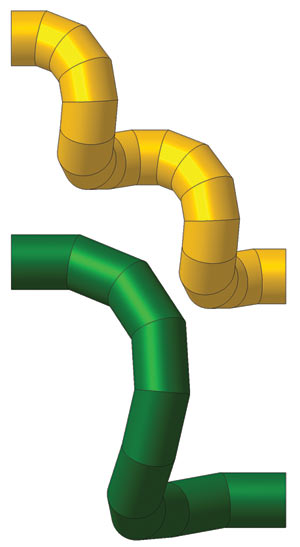
Рис. 3. Спиральные составные компенсаторы (варианты)

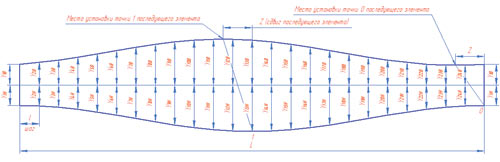
На рис. 4 изображена развертка типового элемента спирального составного компенсатора.

Рис. 4. Развертка типового элемента спирального составного компенсатора

Спиралевидные (квазиспиральные) компенсаторы

Используя широкий спектр выпускаемых промышленностью отводов (сварных, цельных, крутоизогнутых и т.п.), иногда в сочетании с прямыми участками (отрезками) труб, можно выполнить различные по размерам и форме спиралевидные компенсаторы для соединения частей трубопроводов. 3D­модели таких компенсаторов показаны на рис. 5.

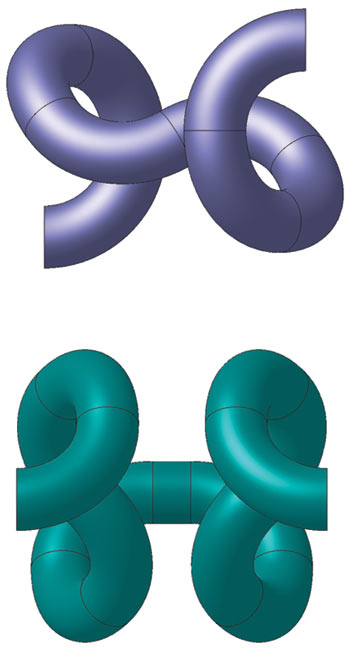
Рис. 5. Квазиспиральные компенсаторы (варианты): а — компенсатор для соединения параллельных стволов трубопровода; б — компенсатор для соединения соосных стволов трубопровода

Моделирование спиралевидных компенсаторов заключается в сборке с необходимыми сопряжениями моделей отводов между собой с определенным (заданным) углом разворота один относительно другого. При этом можно получить бесчисленное множество различных по форме компенсаторов, конфигурация которых определяется расположением соединяемых частей трубопровода.

Спиралевидные компенсаторы просты и недороги в изготовлении.

Выводы

1. Предложена спиральная конструкция компенсатора трубопровода. Приведены формулы для его расчета. Траекторию спирального компенсатора трубопровода рассчитали и построили, используя исходные данные трубопровода. По этой траектории и заданным параметрам компенсатора создали 3D­модель компенсатора. Учитывая положительные свойства спиральных компенсаторов, следует рекомендовать их к использованию наряду с другими видами компенсаторов.
2. Предложена спиральная составная конструкция компенсатора трубопровода. Выведена формула для определения высоты спирального составного компенсатора. Определен ряд выбора числа витков данного вида компенсаторов. Определены особенности их конструкции и расчета. Методом сечений элементов компенсатора получили их развертки. Этот вид компенсаторов также может быть использован для термокомпенсации трубопроводов.
3. Отличаясь простотой моделирования и сборки (изготовления), а также большим спектром формы и размеров, квазиспиральные компенсаторы трубопроводов также могут быть рекомендованы к применению.  

Библиографический список

1. Большая советская энциклопедия. 2­е изд. Т. 35. 1955. 672 с.
2. Чебыкин В.Г. Метод трехмерного моделирования спиральных трубопроводов // Химическое и нефтегазовое машиностроение. 2009. № 10. С. 35­36.
3. Чебыкин В.Г. Спиральные трубопроводы: Справ. // Инженерный журнал. 2010. № 2. С 48­53.
4. Чебыкин В.Г. Беззазорные развертки патрубков: Справ. // Инженерный журнал. 2006. № 9. С. 23­26.

САПР и графика 3`2011