Исследования шарнира шарового шпинделя стана 250
Развитие металлургии тонколистового проката требует повышения эффективности использования технологических машин при высоком качестве листа. Любой механизм или его звено может сыграть существенную роль в обеспечении качества продукции или надежности технологических машин. При эксплуатации стана 250 на ОАО «Северсталь» (г.Череповец) выявилась следующая его особенность: при увеличенных углах перекоса шарового шпинделя наблюдалось увеличение волнистости листа, а также повышение случаев поломки обоймы шпинделя. Потребовалось определить опасные режимы работы шпинделя и предоставить для инженерных сотрудников простые инструменты, которые позволят принять технические решения и планировать технологические операции. Целью исследований ставилось определение безопасных режимов работы шпинделя прокатного стана по параметру плавности движения и безопасного напряженнодеформированного состояния обоймы шпинделя.
Современное развитие вычислительных средств позволяет исследовать поведение механизмов на основе их электронных аналогов (3Dмоделей). Одним из таких инструментов является программный комплекс TFLEX, который среди прочих содержит в своем составе три необходимых для выполняемых работ модуля: TFLEX CAD, TFLEX Динамика и TFLEX Анализ. Зачастую полученные в подобных системах результаты дают более широкую картину происходящих процессов, чем натурный эксперимент. Это обеспечивает получение большего количества инструментов для оптимизации конструкций и в целом более ясное представление об их состоянии и критических параметрах эксплуатации. Проведение натурного эксперимента позволяет получить «точку достоверности», то есть некоторые возможные для натурного эксперимента результаты. При комплексном подходе к исследованиям стало возможно получать необходимую «точку достоверности» не по результатам специально планируемых экспериментов, а по измеренным параметрам текущих технологических процессов. При типовых исследованиях, когда достоверность модели не вызывает сомнений, численные методы позволяют отразить более детальную и плавную картину работы механизмов по всему исследуемому диапазону параметров. При этом экономятся значительные средства и время.

Рис. 1. Пространственная параметрическая модель шпинделя
Для проведения исследований была использована пространственная параметрическая модель шпинделя (рис. 1). Предварительные расчеты показали, что в условиях равномерного распределения сил между шарами шпинделя его обойма имеет многократный запас прочности при заданной нагрузке. Поломка шпинделя была явной причиной неравномерной работы шариков в зацеплении, а возможно, и их подклинивания. Для выяснения картины происходящих процессов необходимо было определить возникающую неравномерность нагружения. Поэтому потребовалось трехэтапное моделирование, включающее геометрический, динамический и прочностной анализ модели шпинделя. Для этой цели оптимально подходил проверенный временем комплекс систем TFLEX, имеющий необходимые приложения. Кроме того, комплекс прост в применении, что обусловлено модульным разделением приложений по задачам, но при этом сохраняется общий формат данных и их ассоциативность. Это оказалось определяющим при выборе. Рассматривались и другие системы, но по параметрам простоты и ассоциативности они оказались неудовлетворительными. Смысл этапов расчета заключался в следующем:
- Построение трехмерной модели шпинделя и определение возможных углов перекоса обоймы относительно вала шпинделя при геометрическом (без нагрузки) замыкании в системе TFLEX CAD.
- В системе TFLEX Динамика для различных углов перекоса определялись силы контактного взаимодействия шаров с пазами обоймы и схема нагружения обоймы для расчета напряженнодеформированного состояния, то есть с какой силой, в какой точке и в каком направлении действует каждый шар. Также в этом модуле определялась неравномерность движения шпинделя при различных углах перекоса.
- В системе конечноэлементного анализа TFLEX Анализ по найденной в TFLEX Динамике схеме нагружения определялись напряженнодеформированное состояние и максимально допустимый крутящий момент.
При исследованиях определялись динамика и напряжения в материале обоймы при различных углах перекоса. Расчет напряженнодеформированного состояния проведен из условия передачи максимального крутящего момента Мкр = 36 кН·м. Для этих условий эквивалентные допускаемые напряжения для материала обоймы «сталь 40ХН» составляют [σэ] = 256 Н/м2 (2560 кГ/см2).
В соосном положении обоймы и вала шпинделя (угол перекоса α = 0°) нагружение шаров является равномерным по окружности зацепления. В этом положении прочность шпинделя ограничивается прочностью трефов втулки, соответствующей ранее определенному максимально допустимому крутящему моменту 86,2 кН·м. Цветовая эпюра распределения напряжений по объему обоймы, построенная системой TFlex Анализ, представлена на рис. 2. Видно, что шаровое зацепление в соосном положении удовлетворяет условиям прочности обоймы с многократным запасом.
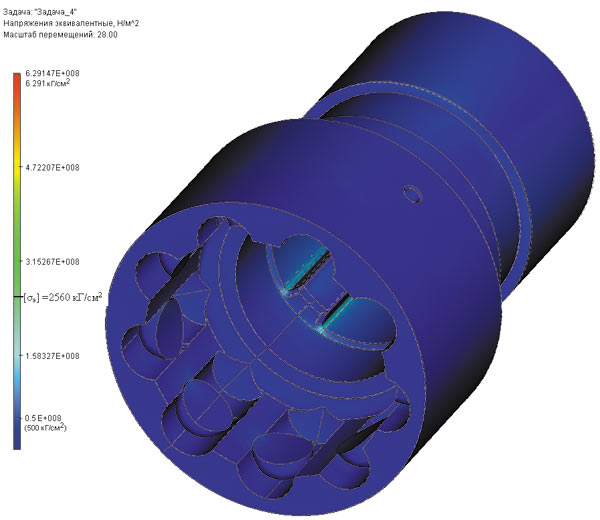
Рис. 2. Распределение напряжений в обойме при ее соосном положении с валом шпинделя и номинальном крутящем моменте 36 кН·м (слева цветовая шкала напряжений; справа — распределение напряжений в обойме)
При геометрическом замыкании шаров с пазами обоймы и втулки с перекосом обоймы относительно вала шпинделя геометрические условия зацепления в шаровой муфте с прямыми цилиндрическими пазами обеспечивают постоянство контакта между нагруженными звеньями (между шарами и пазами обоймы и головки вала). Это условие выполняется благодаря перекатыванию шаров без скольжения вдоль пазов до угла перекоса в 4,5°. При этом положение центров шаров определяется пересечением биссектрисы угла между осями пазов обоймы и вала и биссектрисы угла между нормалью к оси вала в соосном положении и в состоянии перекоса.
Изза больших крутящих моментов, передаваемых шарниром, он выполнен без сепаратора, поэтому при передаче крутящего момента с перекосом обоймы относительно вала на некоторый угол, больший угла трения, под действием выталкивающих сил P от реакций Ro со стороны пазов обоймы и Rв со стороны головки вала происходит скольжение шаров (рис. 3). Скольжение возможно вплоть до упора шара в ограничительную сферическую поверхность паза головки вала. В результате происходит нарушение геометрического условия постоянства контакта шаров с пазами. Нагрузка на шары становится неравномерной, поскольку часть шаров может выйти из зацепления. Определить это состояние какойлибо аналитической системой практически невозможно, а для ручного расчета пришлось бы привлечь целый НИИ. С задачей достаточно просто справилась система TFLEX Динамика. Правда, при построении расчетной и верификационной моделей приходилось активно консультироваться с разработчиками, но результата удалось добиться малыми силами и в короткий срок.
Динамический анализ показал, что при угле перекоса свыше некоторого значения наступает резкое увеличение нагрузок на шары и напряжений в материале обоймы, которое может привести к ее разрушению. Поэтому при исследованиях определяли критический угол перекоса, увеличение которого приводит к превышению допустимых нагрузок (для материала обоймы [σэ] = 2560 кГ/см2).
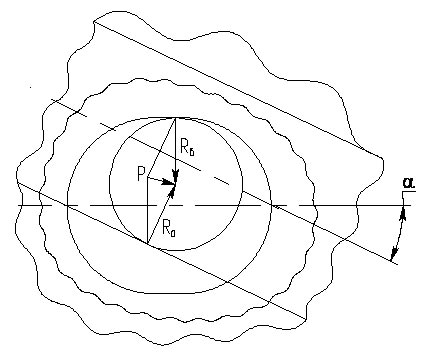
Рис. 3. Положение шара между пазами обоймы и втулки при перемещении со скольжением под действием выталкивающих сил (реакций Ro и Rв)
Для выполнения расчетов в условиях неравномерного нагружения шаров была разработана схема нагружения обоймы, с помощью которой проводились исследования ее напряженнодеформированного состояния, определялись напряжения в материале обоймы и критические (допустимые) углы перекоса α при максимальном крутящем моменте, равном 36 кН·м (3,6 Т·м).
Динамический анализ шарнира шпинделя, состоящего из обоймы, вала и расположенных между ними шаров, был также проведен на построенной трехмерной модели TFLEX.
Исходные данные для расчета: крутящий момент на валу шпинделя, скорость вращения шпинделя, диапазон углов перекоса α (17°), коэффициент трения/скольжения в парах шар — обойма и шар — вал (0,01).
В результате динамического анализа в системе TFLEX Динамика были определены силы, действующие на шары и соответственно на пазы обоймы по окружности зацепления за один оборот шпинделя. На рис. 4 представлены графики нагрузок от шара на паз обоймы за один оборот шпинделя (от 0 до 360°) при углах перекоса обоймы относительно шпинделя 3, 5 и 7°. На графиках также указаны численные значения максимальных нагрузок. Такой характер нагружения пазов обоймы создают последовательно все девять шаров шарнира при работе шпинделя.
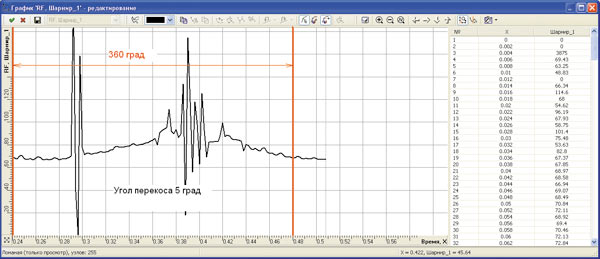
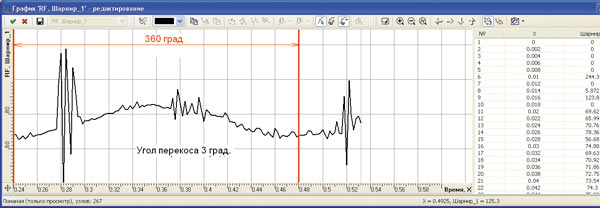
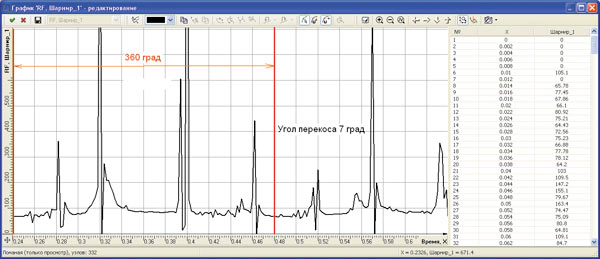
Рис. 4. Распределение нагрузки, действующей на шар за один оборот шпинделя от 0 до 360° (масштаб величин разный — см. на шкалу справа)
На рис. 5 показаны круговые диаграммы распределения этих нагрузок. На диаграмме в виде окружностей представлены значения максимально допустимой нагрузки на шары 175 кН, соответствующей области допустимых нагрузок при работе шарового шпинделя, и нулевой нагрузки. Нагрузка в 175 кН является оценочной и соответствует [σэ] = 2560 кГ/см2. Диаграмма для каждого виртуального испытания автоматически строилась в TFLEX CAD по графикам TFLEX Динамики, для чего использовался специальный индикатор, дающий отсечку графика в исходной точке каждого оборота.
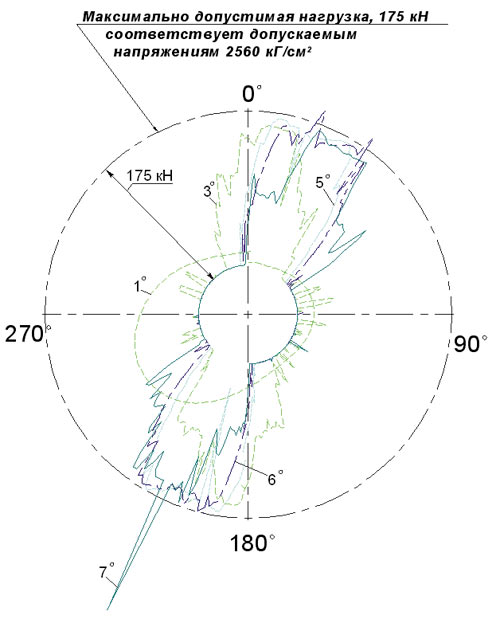
Рис. 5. Круговая диаграмма сил, действующих на шар за один оборот шпинделя при углах перекоса α, равных 1, 4, 5, 6 и 7°
Из рис. 5 следует, что при увеличенных углах перекоса нагружение пазов обоймы каждым шаром на окружности зацепления имеет два явно выраженных периода нагружения в пределах углов поворота шпинделя 1550° и 192220°. В других положениях шары нагружены мало. Следовательно, при работе шпинделя крутящий момент от вала к обойме передается в основном двумя шарами, периодически входящими в пределы указанных углов нагружения и расположенными примерно на центральном диаметре в пределах этих углов со смещением диаметра приблизительно на 1520° от исходного (вертикального) положения при 0° по окружности зацепления.
На основании анализа динамики работы шпинделя были получены графики распределения динамических нагрузок на шары и соответственно на пазы обоймы при заданных углах перекоса. Было показано, что конструкция шарового шпинделя не позволяет достичь равномерной передачи крутящего момента через все шары и пазы обоймы по окружности зацепления при углах перекоса больше 2,5°.
На основании диаграммы для каждого угла перекоса определялось положение обоймы для анализа прочности, исходя из максимальной нагрузки на паз № 1. Для других шаров в найденном положении нагрузка определялась по диаграмме. Так, для угла перекоса в 3° максимальная нагрузка на паз составляет 148 кН, для угла 5° — 170 кН, для угла 7° — 267 кН. На больших углах перекоса подклинивание шпинделя было видно по направлению векторов действия нагрузок при «прокрутке» результатов расчета TFLEX Динамики. Вообще наглядность происходящих процессов является неоспоримым преимуществом систем.
На основании результатов расчета в модуле TFLEX Анализ напряженнодеформированного состояния обоймы для углов перекоса от 1 до 7° были получены: цветовые эпюры распределения напряжений (для углов перекоса 5 и 7° см. рис. 6 и 7), распределения коэффициента запаса прочности, распределения деформаций обоймы.
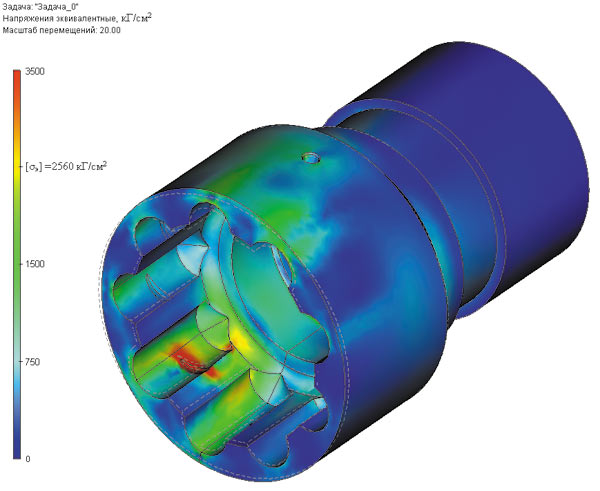
Рис. 6. Распределение напряжений в обойме при угле перекоса относительно вала шпинделя в 5°
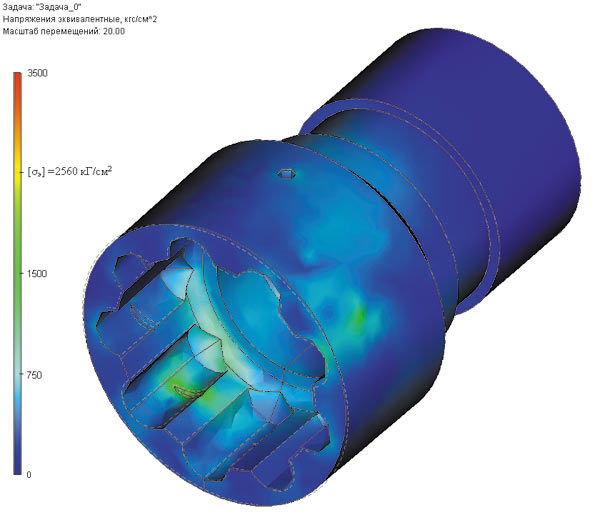
Рис. 7. Распределение напряжений в обойме при угле перекоса относительно вала шпинделя в 7°
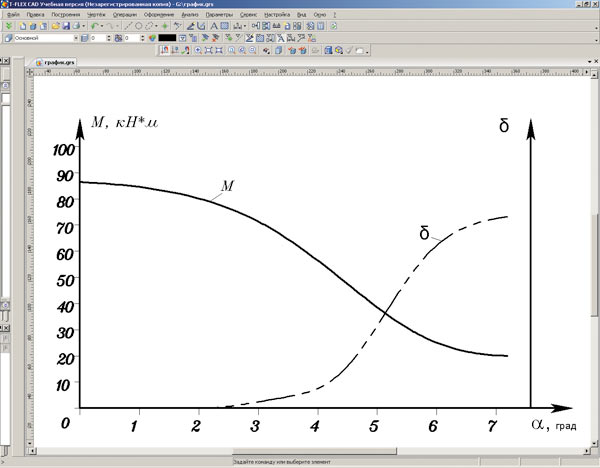
Рис. 8. График нагрузочной способности шарнира М и коэффициента неравномерности вращения δ от угла перекоса α
Благодаря проведенным исследованиям был создан простой инструмент для принятия решений при эксплуатации стана и разработке технологических процессов, что позволило оптимизировать переналадки и повысить эффективность использования оборудования. По сути, результаты исследований свелись к простым графикам: нагрузочной способности шарнира от угла перекоса и коэффициента неравномерности вращения от угла перекоса (рис. 8). При кажущейся простоте этих графиков их параметры определены с достаточной надежностью для принятия технических решений. Определить их на основе только результатов промышленных наблюдений проблематично. А что будет происходить при изменении используемой смазки и ином коэффициенте трения скольжения? Возможно ли применять смазку, отличную от рекомендуемой зарубежными компаниями, без опаски? Очевидно, что натурные исследования обойдутся многократно дороже экономии на смазке и сроках поставки. Однако на эти непростые вопросы можно получить ответ достаточно быстро, используя комплексные инструменты исследования механизмов на базе систем TFLEX.


