Численное моделирование ламинарно-турбулентного перехода на профиле крыла, выполненное в программном комплексе ANSYS CFX

Валерий Вождаев
К. т. н, старший научный сотрудник ЦАГИ им. проф. Н.Е. Жуковского, окончил Московский авиационный институт по специальности «гидроаэродинамика». Работает в направлении, связанном с многодисциплинарным проектированием летательных аппаратов
на основе численных решений уравнений Навье — Стокса и метода конечных элементов

Аэродинамическое качество летательного аппарата, характеризующее его совершенство, определяется как отношение подъемной силы к лобовому сопротивлению. При малом аэродинамическом качестве для летательного аппарата с определенной массой необходима более мощная силовая установка, и для транспортировки той же полезной нагрузки на заданное расстояние потребуется больше топлива, что приводит к увеличению размеров и массы самолета. Чтобы повысить аэродинамическое качество самолета, необходимо при постоянной подъемной силе уменьшить лобовое сопротивление крыла. Одним из способов достижения этого является применение специальных профилей крыла, благодаря которым осуществляется поддержание ламинарного течения в пограничном слое.

Для проектирования ламинаризованных профилей требуются надежные расчетные методы, позволяющие достоверно определить положение ламинарно­турбулентного перехода, поскольку моделирование состояния пограничного слоя в значительной мере влияет на точность расчета коэффициента трения, действующих на аэродинамическую поверхность. В программном комплексе ANSYS CFX (лицензия ЦАГИ № 501024), основанном на численном решении уравнений Навье — Стокса, осредненных по методу Рейнольдса, реализована математическая модель ламинарно­турбулентного перехода, разработанная Р. Лантри и Ф. Ментером [1]. Модель включает четыре дифференциальных уравнения: уравнение переноса для турбулентной кинетической энергии, уравнение переноса для удельной скорости диссипации турбулентной энергии, уравнение переноса для перемежаемости и уравнение переноса для числа Рейнольдса начала ламинарно­турбулентного перехода.

Вышеуказанная модель турбулентности базируется на гибридной модели переноса сдвиговых напряжений (Shear Stress Transport), сформулированной Ментером на основании того, что модели турбулентности типа k­e (k — турбулентная кинетическая энергия, а e — скорость диссипации турбулентной энергии) лучше описывают свойства свободных сдвиговых течений, а модели типа k­w (w — удельная скорость диссипации турбулентной энергии) имеют преимущество при моделировании пристеночных течений [2]. Проведенный анализ показал, что по сравнению с другими используемыми в настоящее время математическими моделями пограничного слоя подход Ментера демонстрирует достаточно высокую эффективность при расчетах характеристик обтекания аэродинамических поверхностей [3].

На основе модели ламинарно­турбулентного перехода Лантри — Ментера вычислены аэродинамические характеристики профиля крыла и проведено сравнение расчетных данных с результатами экспериментальных измерений, выполненных в научно­исследовательском центре NASA [4]. Экспериментальные исследования проводились на модели прямого крыла с профилем GA(W)­1. Модель крыла имеет следующие геометрические параметры: относительная толщина профиля — 17%, размах 0,914 м, хорда — 0,584 м.

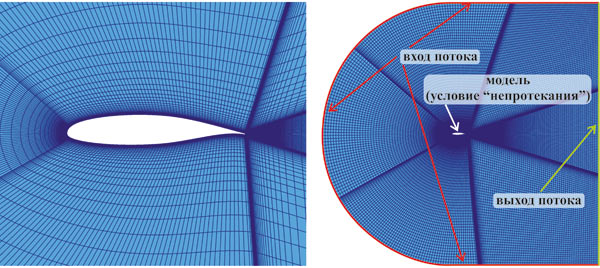
Рис. 1. Структура расчетной сетки вблизи профиля крыла (слева) и на общем виде (справа)

Модуль программы CFX, выполняющий вычисления, базируется на методе конечного объема. При таком подходе для достижения требуемой точности одним из ключевых моментов является построение рациональной расчетной сетки. Высота ячеек в окрестности модели должна быть очень малой (рис. 1), поскольку при недостаточно густой сетке в зоне пограничного слоя расчетное положение ламинарно­турбулентного перехода может смещаться в сторону передней кромки крыла. Расчетная сетка, построенная для рассматриваемого профиля крыла в программе ANSYS ICEM, состоит из 826 800 узлов и 777 024 гексагональных элементов. Высота первой ячейки сетки не превышает 0,01 мм. Для исключения влияния границ расчетной области на точность результатов расчетов эти границы должны быть расположены достаточно далеко от исследуемой модели (см. рис. 1). Высота расчетной области, созданной для проведения представленных в настоящей работе расчетов, равна 10 м, а длина — 11 м.

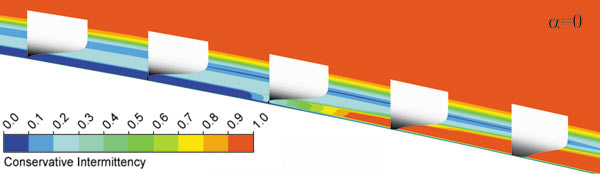
Рис. 2. Профили скоростей и перемежаемость в пограничном слое

Вычисления аэродинамических характеристик профиля крыла выполнялись при числе Рейнольдса 1,9x106 и числе Маха 0,15, что соответствовало условиям, при которых проводились экспериментальные измерения. Следует отметить, что в работе [4], описывающей экспериментальные измерения, отсутствовали данные о степени турбулизации потока в аэродинамической трубе. В связи с этим при проведении расчетов были установлены параметры, соответствующие среднему уровню интенсивности турбулентности потока. В граничном условии на входе потока задана степень турбулентности 5% при отношении динамического коэффициента вихревой вязкости к динамическому коэффициенту вязкости равном 10. В граничном условии на выходе потока использовано среднее статическое давление. Для моделирования двумерного течения на боковых границах расчетной области ставилось граничное условие симметрии. Вычисления проводились в диапазоне углов атаки a от –10° до 15°. Расчеты выполнялись в стационарном режиме (Steady­State). Критерием сходимости являлось достижение величиной среднеквадратичной невязки уровня 10­4.

На рис. 2 показана картина течения в пограничном слое в зоне ламинарно­турбулентного перехода. Коэффициент перемежаемости, равный 0, соответствует ламинарному течению, а коэффициент перемежаемости, равный 1, турбулентному течению. Расчетные профили скоростей показывают, что по мере роста коэффициента перемежаемости профиль скорости в пограничном слое меняет характер от ламинарного (плавное нарастание скорости от нулевого значения) к турбулентному (скачкообразное изменение скорости), что является причиной резкого роста сопротивления трения.

Для сравнения был проведен расчет как при полностью турбулентном течении, так и в условиях свободного ламинарно­турбулентного перехода. Как и следовало ожидать, наибольшее влияние состояние пограничного слоя оказывает на коэффициент сопротивления cx (рис. 3). Следует отметить, что для визуализации коэффициента трения на поверхности модели в CFX­Post необходимо создать выражение, вычисляющее скоростной напор (q), а затем создать переменную, равную Wall Shear X/q.

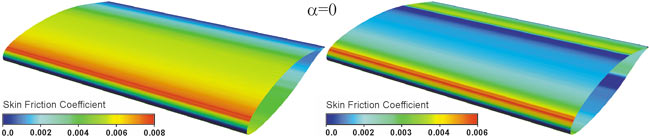
Рис. 3. Распределение коэффициента трения по поверхности крыла при полностью турбулентном течении (слева) и в условиях естественного ламинарно-турбулентного перехода (справа)

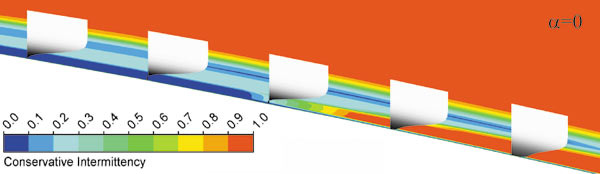
Рис. 4. Интенсивность турбулентности вокруг профиля при полностью турбулентном течении и в условиях естественного ламинарно-турбулентного перехода

Влияние учета ламинарно­турбулентного перехода на характеристики обтекания крыла хорошо видно при сравнении распределения турбулентной энергии, вычисленной при полностью турбулентном течении и с учетом ламинарно­турбулентного перехода (рис. 4). Так же как в случае с коэффициентом трения, для визуализации степени турбулентности в CFX­Post необходимо создать переменную с выражением:

100 x sqrt(2/3 x Turbulence Kinetic Energy)/V,

где V — среднее значение скорости набегающего потока.

Как уже отмечалось, значения коэффициента сопротивления, полученные по программе CFX при полностью турбулентном течении, завышены по отношению к экспериментальным данным (рис. 5). В результате величина аэродинамического качества K в этом случае существенно занижается. Аэродинамическое качество, вычисленное по программе CFX с использованием модели ламинарно­турбулентного перехода, удовлетворительно согласуется с экспериментальными данными (см. рис. 5).

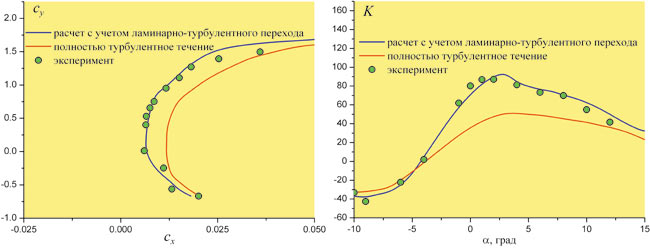
Рис. 5. Поляра профиля крыла (слева) и его аэродинамическое качество (справа)

Таким образом, в результате выполненной работы подробно рассмотрены особенности моделирования процесса ламинарно­турбулентного перехода с использованием программы CFX. Установлено, что расчетные значения аэродинамического качества профиля крыла, вычисленные на основе данной модели, достаточно хорошо согласуются с экспериментальными данными.  

Литература

1. Langtry R.B., Menter F.R. Transition Modeling for General CFD Applications in Aeronautics // AIAA 2005­522, 2005. 14 p.
2. Menter F.R. Two­Equation Eddy­Viscosity Turbulence Models for Engineering Applications // AIAA Journal. Vol. 32. 1994. № 8. P. 1598­1605.
3. Вождаев В.В. Влияние модели турбулентности на точность расчета аэродинамических характеристик механизированного крыла // Техника воздушного флота. 2011. № 3. C. 16­22.
4. McGhee R.J., Beasley W.C. Low­speed aerodynamic characteristics of a 17 percent thick airfoil section designed for general aviation applications // NASA­TN­D­7428. 1973. 69 p.

САПР и графика 6`2012