Оценка прочности и усталостной долговечности конструктивных элементов автомобиля

Алексей Савкин
Д.т.н., профессор; Волгоградский государственный технический университет, декан факультета повышения инженерной квалификации, профессор кафедры сопротивления материалов
Александр Горобцов
Д.т.н., профессор; Волгоградский государственный технический университет, декан факультета электроники и вычислительной техники, профессор кафедры высшей математики
Артем Андроник
Волгоградский государственный технический университет, предполагаемый год защиты магистерской диссертации — 2012

При проектировании конструкций экономически целесообразно использовать САПР. С их помощью можно проверять свойства конструкции до начала производства, повышая ее шансы быть удачной [1 и 2]. Сегодня относительно дешевым, многофункциональным, простым в освоении, обеспечивающим поддержку изделия на всех этапах его жизни — от эскиза до разрушения, обладающим дружелюбным к пользователю интерфейсом программным комплексом является SolidWorks [3], использованный в настоящей работе.

В качестве объекта исследования в данной работе был выбран верхний рычаг подвески автомобиля­внедорожника (рис. 1). В процессе эксплуатации рычаг подвергается воздействию переменных нагрузок, поэтому возникла необходимость провести его прочностной и усталостный анализ c целью выявления областей с наибольшей концентрацией напряжений, а также проверить на предмет возможности образования усталостных трещин и последующего разрушения.

В настоящей работе исследование ограничено стационарными нагружениями. Стационарным случаем нагружения автомобиля считают прямолинейное движение с постоянной скоростью по дороге определенного типа и постоянным коэффициентом сопротивления движению.

Рис. 1. Месторасположение некоторых элементов передней подвески автомобиля: 1 — верхний рычаг подвески; 2 — телескопический амортизатор; 3 — поворотный рычаг; 4 — привод колеса; 5 — балансир; 6 — нижний рычаг подвески

Дальнейшие расчеты связаны с работой в программном комплексе SolidWorks, который является довольно закрытым с точки зрения прозрачности происходящих в нем вычислительных процессов, поэтому следует описать особенности реализации метода конечных элементов в SolidWorks:

• деформации — упруго малые, граничные условия — неизменные в процессе нагружения по величине и по направлению, а жесткость  не зависит от деформаций;
• производится дискретизация объема, занимаемого телом, на элементарные области — конечные элементы;
• узлы конечных элементов располагаются в их вершинах, а также около середин сторон;
• степенями свободы являются перемещения в направлении осей общей для всех узлов в теле системы координат;
• перемещение в пределах каждого элемента аппроксимируется параболической функцией;
• в результате приложения кинематических (перемещений) и статических (усилий) граничных условий тело деформируется, причем нагрузки приводятся к сосредоточенным в узлах; 
• в формулы для расчета компонентов матриц жесткости конечных элементов входят модули упругости и коэффициенты Пуассона;
• матрицы жесткости элементов объединяются в глобальную матрицу жесткости [K]. Столбцы перемещений u, v, w в узлах 1, 2… i… объединяются в общий столбец перемещений [D]. Усилия в направлении осей x, y, z в узлах отдельных элементов суммируются в глобальный столбец усилий [p]. В результате образуется система линейных уравнений, в которой неизвестными являются перемещения: [K][D]=[p];
• глобальная матрица жесткости является разреженной;
• решение соответствует минимуму потенциальной энергии деформированной упругой системы;
• для каждого конечного элемента при наличии перемещений в узлах и аппроксимирующей функции рассчитываются деформации;
• на основе компонентов напряженно­деформированного состояния и параметров прочности вычисляются эквивалентные напряжения по критерию прочности. [3]

Статический анализ в SolidWorks основан на следующих допущениях:

• статическом — нагрузки прикладываются медленно и постепенно, пока не достигнут своих полных величин, поэтому пренебрегают инерционными силами и силами демпфирования;
• допущении линейности —взаимоотношения между нагрузками и вызванными реакциями предполагаются линейными.

В настоящей работе модель верхнего рычага была импортирована в формате STEP в SolidWorks, распознана и преобразована в файл детали.

По всему объему рычага была разбита равномерная сетка из 153 920 тетраэдральных элементов c гранями, аппроксимируемыми параболическими функциями координат, в общей сложности 229 792 узлов. Из двух методов автоматического разбиения сетки, основанных на алгоритмах Делано­Вороного и Форчуна, применен рекомендуемый для несложных конструкций — первый.

Материал исследуемого конструктивного элемента — сталь 40Х [4].

Неотъемлемым элементом конечно­элементного анализа является назначение критериев прочности, их использование и интерпретация результатов расчета напряженно­деформированного состояния. SolidWorks позволяет использовать следующие критерии прочности:

• максимальных эквивалентных напряжений по Мизесу;
• максимальных касательных напряжений;
• Мора­Кулона;
• максимальных нормальных напряжений [5].

Для пластичных материалов рекомендуется применять критерий максимальных эквивалентных напряжений по Мизесу (как в настоящей работе).

После постановки условий решаемой задачи необходимо выбрать решатель. В SolidWorks Simulation в версии 2010 доступны два алгоритма решения системы линейных уравнений:

• прямой метод для разреженных матриц (Direct sparse). Этот метод базируется на алгоритме Холесского с применением компактной схемы хранения матрицы жесткости;
• итерационный компактный метод (FFEPlus). Он основан на разложении Ланшоца и рекомендуется для задач с числом степеней свободы более 300 тыс. (как в настоящей работе).

Кинематические граничные условия были установлены на основе сведений о работе исследуемого элемента подвески, а статические  определены с использованием программного комплекса ФРУНД (в двух вариантах — для единичных продольного и вертикального нагружений).

После запуска и успешного решения соответствующих определенных статических анализов были получены поля напряжений по Мизесу (рис. 2).

Следует отметить, что для разной нагрузки локальные области с концентрацией напряжений различны. Для вертикальной нагрузки это область около правой проушины, а для продольной — около средней проушины. На рис. 2 эти области закрашены темным.

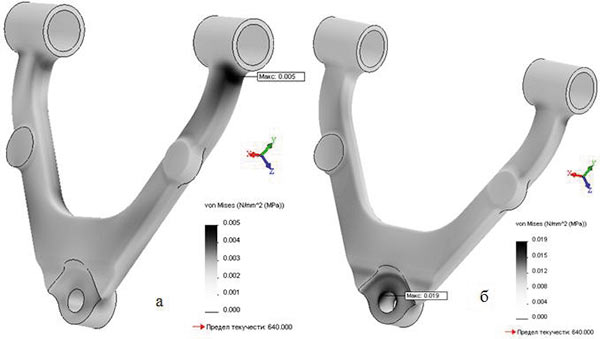
Рис. 2. Поля напряжений для соответствующих граничных условий: а — при продольном нагружении; б — при вертикальном нагружении

Далее приводится описание подготовки и выполнения усталостного анализа в SolidWorks, опирающегося на данные проведенных статических анализов.

Для определения спектров нагружения конструктивных элементов также использовалась математическая модель автомобиля­внедорожника (рис. 3), созданная в среде программного комплекса инвариантного моделирования динамики систем тел ФРУНД [6]. Модель представляет собой набор твердых тел, соединенных упругими и демпфирующими элементами, кинематическими парами. Возмущение от дороги воспринимается через шины, передающими три силы и один стабилизирующий момент.

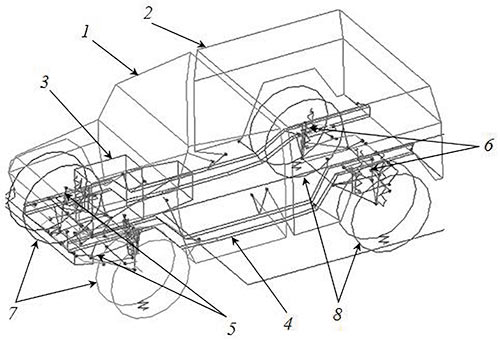
Рис. 3. Расчетная схема автомобиля, полученная в комплексе ФРУНД, с указанием основных систем тел: 1 — кабина; 2 — кузов; 3 — двигатель с коробкой передач; 4 — рама; 5 — элементы передней подвески; 6 — элементы задней подвески; 7 — колеса передней оси; 8 — колеса задней оси

Параметры типичных случайных микропрофилей дорог и методика оценки показателей плавности хода представлены по ГОСТ 12.1.012­2004 ССБТ и ОСТ 37.001.291­84 [7, 8]. Использовались микропрофили динамометрической дороги, ровного булыжника и булыжника с выбоинами автополигона НАМИ. После описания дорожного полотна было выполнено моделирование стационарных случаев нагружения для указанных выше типов дорог. Получены соответствующие спектры нагружения исследуемого рычага в файлах, которые были экспортированы из ФРУНДа в SolidWorks и Mathcad.

На рис. 4 показаны варианты случайного внешнего воздействия в точке крепления передней подвески автомобиля при движении по дорожному полотну. Они были реализованы при изучении частотного спектра в точке крепления передней подвески с помощью ФРУНД. Наибольшее воздействие было оказано дорожным полотном, представленным булыжным покрытием с выбоинами. Максимальная нагрузка за исследуемый промежуток времени — 17,8 кН.

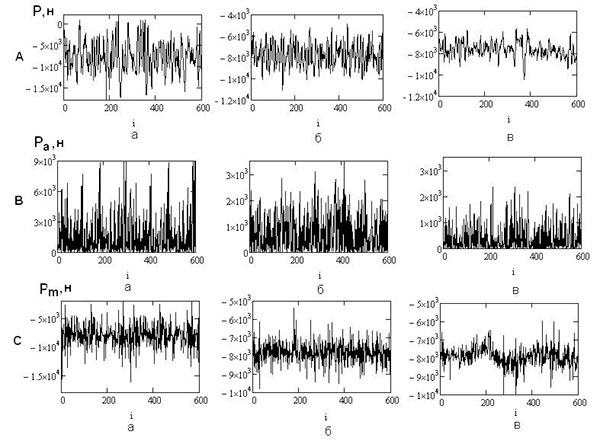
Рис. 4. Случайная выборка нагрузки передней подвески автомобиля для дорожного полотна в точке крепления передней подвески (а — булыжник с выбоинами; б — нормальный булыжник; в — шоссе): исходная нагрузка (А); схематизация по rainflow по амплитуде (В); схематизация по средней нагрузке (C)

При оценке долговечности конструкции случайную выборку внешнего нагружения схематизируют с выделением в выборке циклов, которые могут вносить необратимые усталостные повреждения в структуру металла. В последнее время при прогнозировании ресурса чаще используют метод «падающего дождя» (rainflow), обеспечивающий лучшее соответствие по долговечности для случайной выборки и его схематизированного аналога.

При схематизации случайных процессов по rainflow была получена реализация с разделением процесса по амплитуде и средней нагрузке (рис. 5), где представлены матрицы для вертикальной и продольной нагрузки подвески автомобиля. Матрицы имеют вид гистограмм и точечных матриц c координатами: Ра — амплитудная и Рm — средняя нагрузка. Характеры случайных распределений вертикальной и продольной составляющих нагружения передней подвески различаются. Выборки свидетельствуют о том, что случайное нагружение имеет большую составляющую случайного среднего нагружения, связанную с воздействием веса автомобиля, что приводит к асимметрии циклического напряжения. Таким образом, полученная схематизация описывает двухпараметрическое распределение со случайными величинами Pai и Pmi.

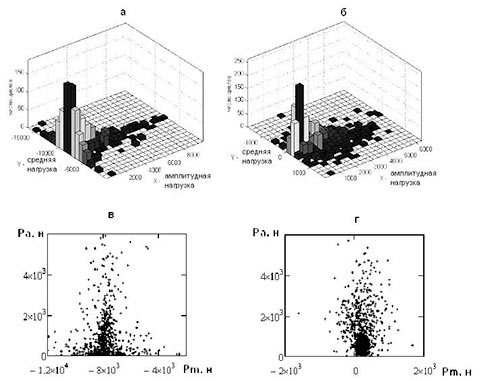
Рис. 5. rainflow-матрица для обобщенной вертикальной (а и в) и продольной (б и г) нагрузки передней подвески автомобиля

В SolidWorks имеется модуль оценки повреждаемости конструктивного элемента при переменных нагрузках от накопления усталостных повреждений. Для вычисления скорректированного переменного напряжения в SolidWorks предлагаются метод Гудмена, метод Гербера (использовался в работе) и метод Содерберга.

Для выполнения исследования на усталость необходимо получить кривую s­N, определяющую значения знакопеременного напряжения относительно количества циклов, требуемых, чтобы вызвать разрушения. В SolidWorks предусмотрена возможность получения кривой s­N на основе кривых усталости для аустенитной или углеродистой стали [9].

Для оценки жизненного цикла конструкции необходимо построение обобщенной случайной выборки нагружения в соответствии с технологическими типовыми циклами работы машины. Предполагая нормальное распределение случайных выборок, мы учли влияние дорожного полотна на обобщенный блок нагружения следующим образом:  булыжник с выбоинами — 68,3%; булыжник нормальный — 27,1%, шоссе — 4,3% [10]. Для оценки повреждаемости используется линейная модель Пальмгрена­Майнера.

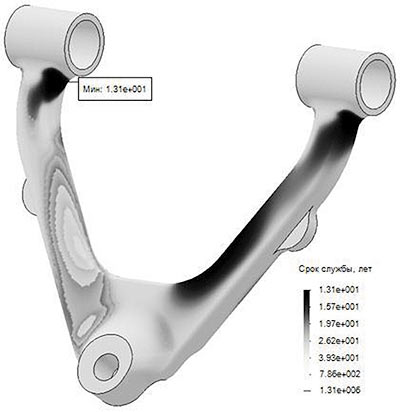
Рис. 6. Эпюра срока службы верхнего рычага передней подвески

По итогам усталостного анализа, выполненного в SolidWorks Simulation, строится эпюра срока службы (рис. 6). На рисунке темным закрашены наиболее опасные места с точки зрения усталостного разрушения. В анализе применялся спектр для вносящего наибольший вклад в усталостное разрушение типа дороги — булыжник с выбоинами. Усталостный срок службы элемента подвески ориентировочно составил 13,1 лет.

Таким образом, можно сделать следующие выводы:

• приведена методика оценки прочности конструктивных элементов транспортных средств с использованием пакетов программ ФРУНД и SolidWorks, позволяющих реализовать полноценный статический и усталостный конечно­элементный анализ конструкции;
• проведенное исследование позволило установить местоположение возможного усталостного трещинообразования и разрушения и вычислить усталостный срок службы элемента подвески транспортного средства. 

Список использованной литературы

1. Савкин А.Н., Андроник А.В. // Анализ прочностных пакетов программ для инженерного расчета конструкции. Материалы 7­й Всероссийской научно­практической конф. Инновационные технологии в обучении и производстве. Камышин.  2010. Т. 5. С. 13­16.
2. Галимянов И.Д., Лавленко А.Л., Валеев И.Д. // Подход к расчету усталостной долговечности несущих элементов конструкции грузовых автомобилей / Проектирование и исследование технических систем: Межвузовский науч. сб. Наб. Челны: ИНЭКА. 2007. С. 62­73
3. Алямовский А.А., Собачкин А.А., Одинцов Е.В. и др. SolidWorks 2007/2008. Компьютерное моделирование в инженерной практике / СПб.: БХВ­Петербург, 2008. 1040 с.
4. Марочник сталей и сплавов / В.Г. Сорокин, А.В. Волосникова, С.А. Вяткин; Под общ. ред. В.Г. Сорокина. М.: Машиностроение, 1989.  640 с.
5. Аликин В.Н., Анохин П.В., Колмогоров Г.Л. и др. Критерии прочности и расчет механической надежности конструкций / Пермский государственный технический университет.  Пермь, 1999.  158 с.
6. Горобцов А.С. Программный комплекс моделирования пространственного движения систем твердых и упругих тел // Инженерный журнал. 2004. № 9.  С. 29­36.
7. ГОСТ 12.1.012­2004 ССБТ. Вибрационная безопасность. Общие требования.  М.: Стандартинформ, 2008.  15 с.
8. ОСТ 37.001.291­84. Автотранспортные средства. Технические нормы плавности хода.  М.: Изд­во стандартов, 2000. 25 с.
9. Алямовский А.А. SolidWorks/COSMOSWorks. Инженерный анализ методом конечных элементов. М.: ДМК Пресс, 2004.  432 с.
10. Черников С.К., Черников С.К., Ашихмин А.Н. Математическая модель для анализа НДС рамы автомобиля
    КамАЗ и ее верификация / Казанский физико­технический институт // Ежегодник. Казань: ФизтехПресс, 2001. С. 187­193.

САПР и графика 8`2012