Сеточный генератор ANSYS Maxwell

Алексей Клявлин
Инженер технической поддержки отдела инженерного анализа, ГК «ПЛМ Урал»—«Делкам-Урал»

Данный материал является продолжением серии статей, посвященных программному комплексу ANSYS. На этот раз объектом внимания выступает сеточный генератор, реализованный в инструменте моделирования электромагнитного поля ANSYS Maxwell. Данный продукт более предпочтителен перед аналогами за счет сочетания широты возможностей и простоты освоения. Умение оптимально использовать минимальный набор опций сеточного генератора, предусмотренный разработчиками программного обеспечения, — залог точности полученных результатов при моделировании электромагнитного поля методом конечных элементов.

Основные сведения

Метод конечных элементов (Finite Element Method) — довольно серьезное средство, широко используемое инженерами, учеными и исследователями для решения технических задач, возникающих в электромагнитных, тепловых, прочностных, гидродинамических и акустических полях. МКЭ — явно доминирующий численный метод анализа для моделирования распределения физического поля, по успешности не сравнимый с любым другим численным методом (рис. 1).

Как правило, МКЭ находит решение для любой технической задачи, которая может быть описана конечным набором пространственных уравнений в частных производных с определенными границами и начальными условиями. Данный метод решения задач имеет твердую теоретическую основу. Она базируется на математических теоремах, гарантирующих асимптотическое стремление результата расчета поля к единственно возможному решению при уменьшении размеров конечных элементов, используемых в процессе решения. Для решений во временной области пространственная дискретизация задачи должна улучшаться пропорционально временному шагу расчета, долженствующему соответствовать предполагаемым временным константам задачи (таким как постоянная времени магнитной диффузии).

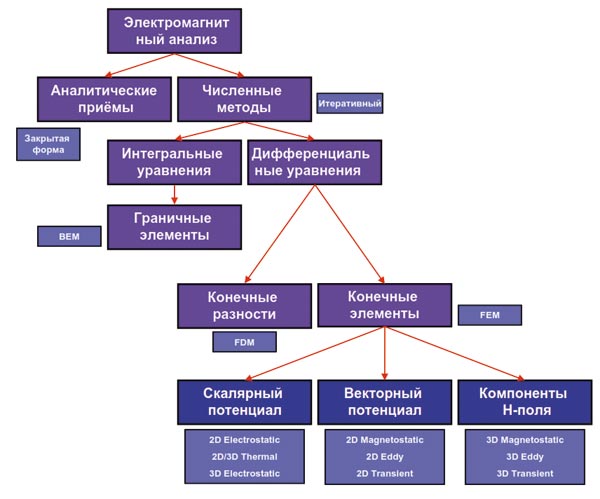
Рис. 1. Различные методы для анализа электромагнитного поля. Каждый метод имеет свои сильные и слабые стороны

Реализация решения задач в ANSYS Maxwell

ANSYS Maxwell решает задачи электромагнитного поля, используя уравнения Максвелла в конечной области пространства с соответствующими граничными условиями и определенными пользователем начальными условиями, чтобы получить гарантированно единственное решение. Проще говоря, электродинамическая задача сводится к решению системы алгебраических уравнений для определения неизвестных коэффициентов. Для этого геометрия задачи автоматически разбивается на четырехгранные и треугольные элементы для трехмерной и двухмерной задачи соответственно. Все эти объемные или плоские объекты модели автоматически объединяются в одну цельную структуру сеточным генератором (Mesher). Набор всех тетраэдров или треугольников называется сеткой конечных элементов модели или просто сеткой (рис. 2).

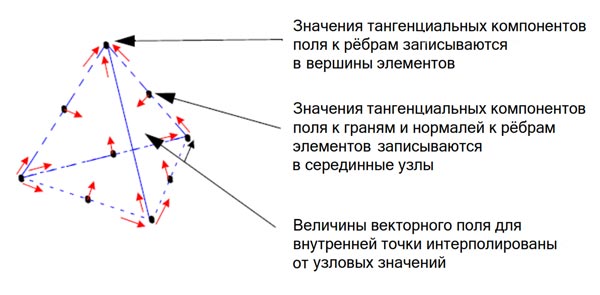
Рис. 2. Тетраэдрический 10-узловой конечный элемент

Как только генератор сетки конечных элементов дискретизирует пространство, создается большая разреженная матрица уравнений

[S][H] = [J] (SparseMatrix), где [J] — источник магнитного поля, [H] — искомое магнитное поле, [S] — значения неизвестных коэффициентов. Для решения подобных уравнений используются стандартные техники решений матриц: Sparse Gaussian Elimination (прямой решатель), Incomplete Choleski Conjugate Gradient Method (ICCG итеративный).

В результате решения воссоздается общая картина поля с помощью методов аппроксимации и с использованием квадратичной полиномиальной базисной функции второго порядка для каждого элемента

(Hx(x,y,z) = a0 + a1x + a2y + a3z + a4xy + a5yz + a6xz + a7x2 + a8y2 + a9z2).

В трехмерном моделировании для получения базисной функции для каждого тетраэдра определяются величины поля для десяти точек (узлы в вершинах и промежуточные реберные узлы).

Технология адаптивного улучшения сеточной модели

Равносторонние тетраэдры и треугольники лучше всего работают с квадратичной интерполяцией второго порядка, которая используется между узлами. Поэтому следует иметь в виду, что желательно производить расчет на относительно однородной равносторонней сеточной модели. Особое внимание необходимо уделить локальным областям с резким пространственным градиентом поля. Для повышения точности решения в данном случае пространственная дискретизация модели должна быть максимальна.

Говоря о задачах моделирования магнитного соленоидального поля, зачастую сложно предвидеть наверняка, насколько подробным и в каком именно месте должно быть локальное сгущение сетки конечных элементов. Пользователю необходимо найти допустимый компромисс между временем решения задачи и точностью полученных результатов. Данная проблема решается в технике адаптивного улучшения сеточной модели, основыванной на локальном определении ошибки вычисления.

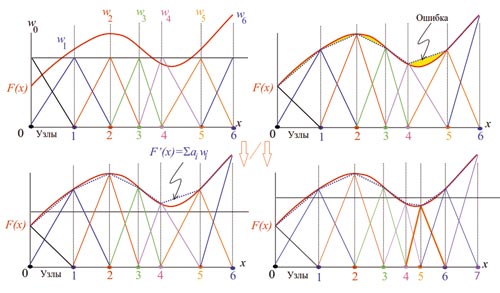
Рис. 3. Схематичное представление техники адаптивного усовершенствования сеточной модели

На рис. 3 метод конечных элементов используется для аппроксимации неизвестной кривой F(x). Модель дискредитирована 6­ю отдельными ячейками. w0­w6 являются кусочно­линейными «основными функциями», из которых будет построено приблизительное решение. В МКЭ неизвестная функция выражена как взвешенная сумма кусочно­непрерывных основных функций. Приблизительным решением МКЭ является ломаная функция F ’(x), показанная пунктиром. Главной особенностью МКЭ, реализованного в ANSYS Maxwell, является способность определить ошибку в местном масштабе. Напомним, что F(x) неизвестен, но, тем не менее, ошибка может быть определена (Cendes, Z.J., and D.N. Shenton. Adaptive mesh refinement in the finite element.; IEEE Transactions on magnetics (T­MAG), Pages 1811­1816 , Volume 21, Issue 5, Sept 1985). Далее следует увеличение плотности сетки в областях наибольшей ошибки, и решение будет выполнено на сеточной модели, обеспечивающей максимальную точность с наименьшим количеством возможных элементов.

Алгоритм адаптивного улучшения сеточной модели реализован для всех задач моделирования электромагнитного поля, кроме расчета нестационарного магнитного и электрического поля (рис. 4). Погрешности результатов в данном случае будут зависеть от качества сетки, созданной пользователем с применением сеточных опций (Mesh Operations). В большинстве случаев адаптивный, итеративный процесс расчета может быть ускорен посредством введения вышеупомянутых операций на этапе построения начальной сетки.

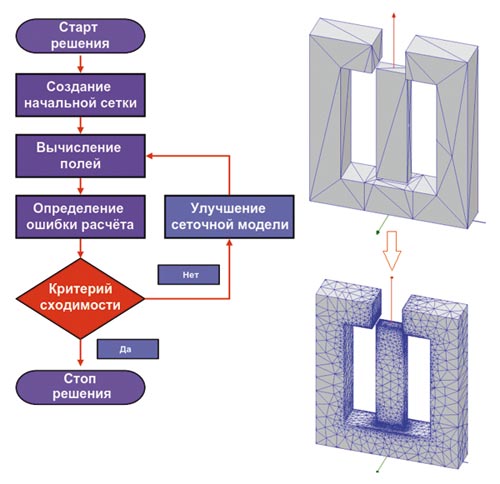
Рис. 4. Алгоритм адаптивного улучшения сеточной модели

Сеточные опции

Запуск полевого решения возможен при наличии начальной сетки в расчетной области, которая создается без каких­то инструкций от пользователя. Если какая­либо пространственная дискретизация уже существует, Maxwell не создаст начальную сетку и будет использовать существующую (рис. 5).

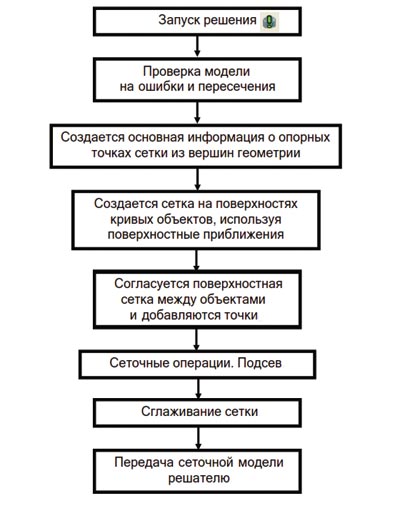
Рис. 5. Автоматический процесс создания сеточной модели

Начальная сетка создается исключительно на основании геометрии модели, и сеточный генератор не имеет представления о пространственной конфигурации поля, так как еще нет начального решения задачи. Поэтому плотности сетки в интересующих местах недостаточно для выполнения точного решения. Ручное введение сеточных операций — хороший способ избежать такой ситуации при создании начальной сетки.

Кратко опишем несколько дополнительных инструментов для работы с начальной сеткой:

• Length Based Mesh Operations — разбиение на основании длин сторон треугольного или тетраэдрического элемента. Наверное, основное базовое средство для обработки модели. Опция ограничивает длину ребер элементов и может быть применена к поверхности или ко всему объему модели. Также есть возможность указания максимального числа тетраэдров, которые будут добавлены во время уплотнения сетки разбиения;
• Skin Depth Based — разбиение на основании глубины скин­слоя. Эта опция применима как к длинам сторон элементов на поверхности, так и к уплотнению сетки в глубь выбранной поверхности. Этот метод применим в первую очередь для объектов с индуцированными вихревыми токами в пристеночной области. Удобный калькулятор расчета глубины проникновения поля автоматически определяет размер поверхностного элемента, глубину и количество слоев на основании введенных данных (частота, проводимость, относительная магнитная проницаемость);
• Surface approximation — опции настройки представления кривых поверхностей. Поверхности объектов в ANSYS Maxwell могут быть плоскими, цилиндрическими или коническими, тороидальными, сферическими или сплайнами. Сами поверхности модели называются реальными поверхностями (true surfaces). В процессе перехода от реальных поверхностей к сеточной модели сеточный генератор использует метод аппроксимации кривых поверхностей линейными отрезками. Интерфейс позволяет пользователю определять алгоритм построения сетки, используемый для начального разбиения: более новая и устойчивая технология построения объемной сетки TAU mesher (со строгой или нестрогой аппроксимацией поверхности), Ansoft Classic mesher, «Auto» (установка по умолчанию). При установке по умолчанию программное обеспечение на основе экспертизы модели решает, какой алгоритм построения сетки использовать.

Если поверхности объектов скругленные (рис. 6), то плоские стороны тетраэдра лежат на небольшом расстоянии от реальной поверхности объекта (surface deviation), и оно измеряется в единицах длины модели. Отклонение поверхности больше вблизи центра треугольника и меньше вблизи углов вертикали.

Нормаль к кривой поверхности меняется в зависимости от места приложения, но она постоянна для каждого треугольника. В этом контексте «нормаль» определяется как линия, перпендикулярная поверхности, а разность углов между нормалью кривой поверхности и соответствующей поверхности ячейки называется отклонением нормали (normal deviation) и измеряется в градусах.

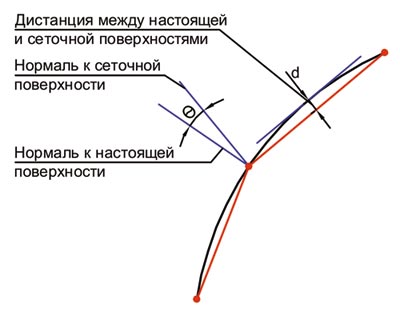
Рис. 6. Пояснения к опциям представления кривых поверхностей

Аспект отношения треугольников (aspect ratio), используемых в плоских поверхностях, равен отношению радиуса, описывающего треугольник снаружи, к радиусу вписанной окружности. Она равна единице для равностороннего треугольника и приближается к бесконечности, когда треугольник становится более тонким.

Модифицировать можно параметры отклонения поверхности, максимально разрешенное отклонение нормали и максимальный формат.

Опция Model Resolution определяет самые маленькие детали в модели, которые программа разбиения должна фиксировать и связывать сеткой. Обычно анализ начинается с уже подготовленной геометрии в сторонних CAD­редакторах, содержащей большое количество дополнительных элементов, которыми можно пренебречь в анализе поля. Данная опция хорошее средство для таких целей. Пользователю необходимо только указать объект и назначить допуски. Значение по умолчанию Model Resolution = 100?Ѕ?предел допуска ACIS (рис. 7).

Рис. 7. Результаты расчета магнитного поля в электрической модели на начальной и усовершенствованной сеточной модели

Описанная в статье техника работы с сеточной моделью активно развивается: оптимизируется сам сеточный генератор, вводятся новые функции и инструменты. Для более детального подхода к решению задач и получения актуальной информации по данным вопросам рекомендуем обращаться к специалистам группы компаний «ПЛМ Урал»—«Делкам­Урал» или задавать вопросы на форуме нашего сайта. Всегда будем рады помочь.

САПР и графика 4`2013