О методологии компьютерного проектирования трасс линейных сооружений

Валерий Струченков
Д.т.н., профессор Московского государственного технического университета радиотехники, электроники и автоматики (МГТУ МИРЭА)

Введение

Линейные сооружения (дороги, трубопроводы, каналы и др.) — это такие сооружения, положение которых на местности определяется их осью, то есть трассой. Трасса — это трехмерная кривая, которая традиционно представляется двумя плоскими кривыми: планом и продольным профилем. План трассы (часто его называют трассой) — это проекция трассы на горизонтальную плоскость, а продольный профиль — это зависимость координаты Z (s) от длины в плане. Продольный профиль получается при развертке на плоскость вертикальной поверхности, проходящей через трассу. Пересечение этой вертикальной поверхности с поверхностью земли дает продольный профиль земли по трассе (черный профиль), а трасса при развертке дает проектную линию (красный профиль).

Проектирование трассы, таким образом, сводится к двум взаимосвязанным проектным задачам: проектированию плана и продольного профиля.

На положение трассы на местности влияют различные факторы: рельеф земли, геологические, гидрологические, климатические условия, наличие других коммуникаций и запрещенных зон (например, по требованиям экологии).

В условиях равнинного рельефа особых сложностей в проектировании трасс, как правило, не возникает. Исключение могут составлять районы со сложной геологией и наличием большого числа контурных ограничений в виде запрещенных зон, развитой инфраструктуры и др. В обжитых районах положение трассы в плане  может практически однозначно определяться условиями землепользования, и задача поиска трехмерной кривой превращается в задачу проектирования плоской кривой, то есть проектирования продольного профиля по одному или нескольким возможным вариантам плана трассы.

Как правило, в условиях пересеченного рельефа задача существенно осложняется и возникает вопрос о поиске оптимального варианта трассы, то есть проектирования плана и продольного профиля в их взаимосвязи. Этот вопрос осложняется наличием целого ряда технических ограничений и нормативов, так как план и продольный профиль трассы должны состоять из элементов определенного вида, параметры которых ограниченны.

В настоящее время для таких сооружений, как железные и автомобильные дороги, не существует математических моделей и алгоритмов проектирования трассы как пространственной кривой, то есть совместного проектирования плана и продольного профиля.

Предложены различные подходы к использованию возможностей современных компьютеров для проектирования плана и продольного профиля трасс линейных сооружений.

Рассмотрение этих подходов с позиций современной теории систем и теории оптимизации является целью настоящей статьи.

Особенности поиска оптимальных трасс

Главная особенность рассматриваемой задачи применительно практически к любому из линейных сооружений — это чрезвычайная сложность ее формализации и построения математической модели, то есть сведения проектной задачи к математической задаче  оптимизации. Дело в том, что реально приходится рассматривать целый комплекс взаимосвязанных проектных задач. Так, применительно к проектированию дорог во взаимосвязи с проектированием плана и продольного профиля должны решаться задачи проектирования поперечных профилей  земляного полотна, проектирования водопропускных и других искусственных сооружений, распределения земляных масс и выбор способов производства земляных работ и др. Формализовать все это в единой математической модели крайне сложно. Практически каждая из упомянутых проектных задач, в свою очередь, является задачей оптимизации.

Следующая особенность рассматриваемой задачи состоит в том, что число элементов плана и продольного профиля неизвестно. Так, продольный профиль новой железной дороги проектируется в виде ломаной, звенья которой должны удовлетворять ограничениям по минимальной длине, уклонам и разностям уклонов смежных элементов, но число этих элементов неизвестно, равно как и число элементов плана трассы. Получается задача оптимизации неизвестной размерности. Подобные задачи не вписываются в одно из наиболее общих направлений современной теории оптимизации — нелинейное программирование.

Необходимо отметить также и взаимосвязь элементов трассы, которая, как правило, не позволяет разбить проектируемый объект на отдельные локальные участки. Например, при проектировании трасс новых железных дорог объектом проектирования является железнодорожный перегон ( 25­30 км и более).

При проектировании автодорог в условиях пересеченного рельефа также приходится рассматривать участки значительной протяженности.

Наконец, отметим и наличие неформализуемых факторов, например, оценки экологических и социальных последствий строительства.

Не приспособлена к формализации задачи и нормативная база. В строительных нормах и правилах содержатся нормы проектирования для обычных, сложных и особо сложных условий, а сами эти понятия не определены.

Различные подходы к автоматизации проектирования трасс линейных сооружений

В современных САПР линейных сооружений [1­4] проектирование трасс осуществляется в интерактивном режиме. При этом проектные решения задаются проектировщиком, а компьютер используется для решения вспомогательных задач расчетно­графического характера.

Такой подход был реализован еще в 60­х годах прошлого века в развитых странах Запада.

В то  время в СССР не было технической возможности организации интерактивного процесса проектирования плана и продольного профиля. Было избрано направление формализации проектных задач в математических моделях и разработки алгоритмов поиска проектных решений на основе математических методов оптимизации. Были решены отдельные проектные задачи, например оптимальное распределение земляных масс, на основе линейного программирования [5]. Была решена также задача проектирования продольного профиля железных и автомобильных дорог при заданном плане трассы на основе динамического программирования [6] и нелинейного программирования [7]. Однако в силу ряда причин главенствующим направлением в дальнейшем стало задание проектных решений проектировщиком в процессе интерактивного проектирования.

Известна высокая стоимость строительства таких сооружений, как дороги, в сложных условиях. Возникает вопрос, достаточно ли для поиска оптимальных решений интуиции и опыта проектировщика.

В поисках ответа на этот вопрос еще в 1976 году Ю.С. Карих организовал и осуществил уникальный эксперимент [8], проводившийся в два этапа.

На первом этапе был выбран участок продольного профиля протяженностью 5 км  по трассе автомобильной дороги, проходящей по пересеченной местности с перепадом отметок 54 м. Предлагалось запроектировать продольный профиль по нормам третьей технической категории. Преднамеренно были приняты упрощенные условия: грунт однослойный — супесь на всем протяжении, поперечный уклон местности отсутствует, поперечные профили земляного полотна — типовые, указаны пункты размещения водопропускных труб, минимальные высоты насыпей в этих пунктах, а также проектные отметки в начальной и конечной точках профиля.

В эксперименте анонимно участвовали 14 проектировщиков из различных организаций со стажем работы от 8 до 38 лет. Подробно исходные данные и количественные результаты эксперимента приведены в [8].

Характерно, что в некоторых точках профиля расхождения по вариантам превышали 8 м, отклонения по стоимости достигали 35%, а в объемах земляных работ — 40% [8].

На втором этапе продольный профиль того же участка с теми же исходными данными, но вычерченный в обратном направлении (конечная точка стала началом, а начальная конечной) через год был предложен тем же специалистам. Расхождения между полученными вариантами были примерно такими же. Варианты предоставлялись анонимно, но спустя некоторое время один из специалистов вспомнил, что год назад он проектировал этот же профиль. Расхождения между его вариантами в одних и тех же точках достигали 2 м.

Необходимость оптимизации проектных решений по таким сложным и дорогостоящим сооружениям, как железные и автомобильные дороги, не должна вызывать сомнений. Интуиции и опыта проектировщиков для этой цели явно недостаточно.

Конечно, возможность визуализации и выработки проектных решений в интерактивном режиме с использованием современных компьютеров способствует повышению качества проектирования. Но ограниченные размеры экрана и необходимость корректировки отдельных участков без учета их взаимосвязи с соседними участками создают дополнительные сложности. Как показали расчеты по различным программам решения относительно простой задачи проектирования плана реконструируемой железной дороги (выправка пути), именно локальный подбор приводит к нарушению нормативов и другим нестыковкам.

Казалось бы, для поиска оптимальной трассы, используя быстродействие современных компьютеров, достаточно рассмотреть большое число вариантов. Так, в [9] сообщается, что система Trimble Quantm определяет расходы и просчитывает миллионы возможных маршрутов в соответствии с заданными ограничениями, чтобы выбрать и представить на рассмотрение проектировщика от 10 до 50 оптимальных вариантов». Очевидно, под маршрутами в [9] понимаются  варианты положения трассы в плане. Поскольку в [9]  не упоминается проектирование продольного профиля по каждому маршруту (где, в свою очередь, есть множество вариантов), можно понять, что решается  известная «плоская» задача трассирования, в которой область поиска разбивается на элементы и в каждом из них задаются затраты на строительство дороги в расчете на единицу длины. Такая задача имеет смысл только для проектирования в  условиях равнинного рельефа. Она была решена еще в 60­х годах прошлого века с применением динамического программирования [10].

Что касается решения этой задачи перебором миллионов возможных вариантов, решающее значение имеет способ назначения этих вариантов. Очевидно, это должен делать компьютер, но полный перебор вариантов невозможен даже на мощных современных компьютерах. В реальных проектных задачах миллион рассмотренных вариантов  составляет ничтожную часть от общего числа возможных вариантов. Покажем это на примере частной задачи: проектирование продольного профиля по заданному варианту плана трассы. Очевидно, что при переборе и в плане, и в профиле число вариантов будет гораздо больше.

Проектная линия продольного профиля имеет наиболее простой вид при проектировании железной дороги. Она представляет собой ломаную, элементы которой удовлетворяют ограничениям по минимальной длине, уклонам и разностям уклонов смежных элементов.

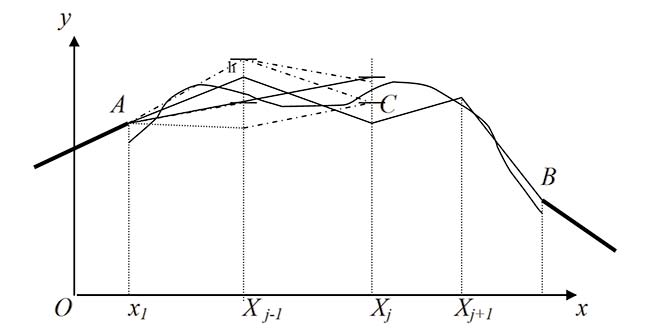
Рис. 1. К оценке числа вариантов проектной линии

Предположим, что длины элементов нам известны (рис. 1) и оценим число возможных вариантов решения задачи, то есть проектных линий.

Теоретически число вариантов бесконечно. Но при дискретном поиске по вертикали с дискретом h это число вариантов зависит от числа дискретов, то есть возможных положений конечной точки очередного элемента и числа элементов.

В реальных проектах проектные отметки определяют с точностью до 0,01 м. Возьмем
h = 0,1 м, то есть на порядок грубее. Далее, ширина области поиска, то есть разность максимальной и минимальной возможных отметок концов каждого элемента в условиях пересеченного рельефа достигает нескольких десятков метров. Примем 10 м. Получается, что на каждой вертикали рис. 1 имеем k = 100 точек. При полном переборе имеем более k^n–1 вариантов, где n — число элементов, которое при минимальной длине элемента 200 м и длине участка всего 5 км составит 25. В итоге получаем 100²⁴ или 10⁴⁸.

Если учесть, что в реальных условиях длины элементов неизвестны и будет осуществляться  перебор их значений с шагом d, то при числе шагов в пределах длины одного элемента m получаем оценку числа вариантов (mk)^n–1.  Реально d = 10 м и m > 10. В итоге получаем оценку числа вариантов 10⁷². Конечно, не все варианты допустимы по ограничениям, и число допустимых вариантов существенно зависит от предельных значений уклонов элементов и разностей смежных уклонов. Однако, учитывая только допустимые варианты, их число меньше полученной величины на несколько порядков, но по сравнению с ней миллион действительно является малым числом.  Тем более при варьировании и в плане, и в профиле. Поэтому  утверждение в [10]: «…такой подход позволяет быстро показать, что рассмотрены все приемлемые варианты, как того требуют правила проектирования и финансового менеджмента», — требует уточнений.

Характерно, что не только перебор случайно назначаемых вариантов, но и динамическое программирование при такой ширине области варьирования и дискретов поиска оказывается бесполезным из­за вычислительных сложностей. Эта ситуация известна как «проклятие размерности».

Не приводит к успеху и локальный подход, то есть поочередное варьирование отдельных элементов трассы в силу отмеченной ранее взаимосвязи элементов.

Так, в [11] рекомендуется следующее: «Для выбора оптимального радиуса кривой R в трудных топографических условиях следует протрассировать три варианта при разных радиусах, определить строительную стоимость и эксплуатационные расходы участка дороги между общими точками и подсчитать для всех вариантов приведенные строительно­эксплуатационные расходы Эпр. Построив график зависимости Эпр(R), можно найти оптимальный радиус, соответствующий минимуму показателя Эпр». В [11] приводится пример, показанный на рис. 2. Нами добавлена пунктирная линия.

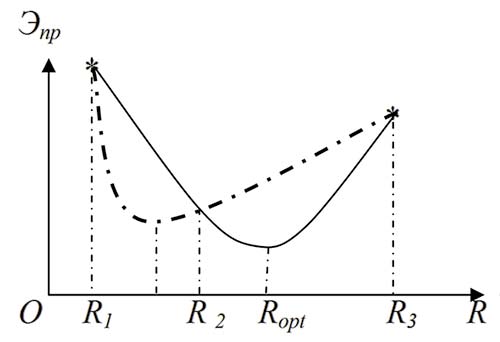
Рис. 2. Определение оптимального радиуса

Возникает вопрос, а какую кривую надо строить по трем точкам, чтобы найти минимум?  Таких кривых бесконечно много. Если строить параболу, то почему она должна иметь минимум, а не, например, максимум на рассматриваемом интервале? Вообще при увеличении радиуса приведенные затраты не обязательно уменьшаются и все три точки могут соответствовать увеличению приведенных затрат при увеличении радиуса. Неслучайно именно в сложных условиях используются минимально допустимые радиусы кривых в плане.

Далее — как выделить этот локальный участок с единственным варьируемым параметром? Если меняется радиус, то почему не меняется угол поворота и его вершина или длины переходных кривых (клотоид) слева и справа? Наконец, при изменении радиуса меняется продольный профиль. О том, как проектировать продольный профиль на компьютере, в [11] не сообщается. Рассмотренная рекомендация могла бы иметь смысл в докомпьютерную эпоху. А сейчас, если мы умеем рассмотреть и обсчитать три варианта, то почему только три, а не гораздо больше, и не выбрать лучший вариант без построения каких­либо графиков? Дело не в количестве вариантов, а в бесперспективности самой идеи локального варьирования элементами трассы, особенно в сложных условиях.

Комплексное применение математических моделей и методов оптимизации

При разработке САПР плана и профиля новых железных дорог нами был использован подход, основанный на следующих принципах:

• не имея математических моделей трехмерной задачи трассирования, следует оставить назначение вариантов плана трассы проектировщику. Лучше группе проектировщиков, так как каждый независимо от других может предложить свой вариант;
• по заданным вариантам плана трассы должно выполняться компьютерное проектирование продольного профиля во взаимной увязке с проектированием поперечных профилей земляного полотна, проектированием искусственных сооружений, распределением земляных масс и выбором способов производства работ. Соответствующая схема выполнения расчетов с их многократным повторением и компьютерной корректировкой проектной линии  описана в [12, 13];
• в этой многоэтапной схеме используется иерархия математических моделей с уточнением их параметров по мере решения смежных проектных задач. Вычисление критериальной функции и сравнение вариантов плана трассы происходит после каждого очередного этапа. Отбраковка вариантов плана трассы возможна после любого этапа, если она становится очевидной;
• в силу отмеченной неизвестной размерности задачи приходится сначала рассматривать проектную линию в виде ломаной, составленной из коротких элементов, и выполнять расчеты по ее оптимизации [13]. При этом используются методы нелинейного программирования. Затем выполняется преобразование полученной ломаной линии в проектную линию, элементы которой удовлетворяют ограничению по минимальной длине. Это делается по алгоритму динамического программирования, так как отклонения от исходной ломаной не превышают 0,5 м. Тем самым определяется размерность задачи. На заключительных этапах оптимизируется положение этой ломаной. При этом используется тот же алгоритм нелинейного программирования, что и на начальном этапе.

Наличие обратных связей, использование только математически корректных алгоритмов оптимизации — принципиальная особенность разработанной САПР.

Характерно, что при размерности задачи до 1000 переменных и 4000 ограничений алгоритм решает ее не более чем за 5000 итераций, то есть рассматриваются не миллионы, а только тысячи вариантов. 

Список литературы:

1. Shafahi Yousef, Shahbazi M.J. «Optimum railway alignment» http://www.uic.org/cdrom/2001/wcrr2001/pdf/sp/2_1_1/210.pdf.
2. CARD/1. URL: http://www.card­1.com/en/home/
3. Курилко Ю., Чешева В. Geonics ЖЕЛДОР­ САПР // CADmaster. № 1(36). 2007.
4. Тоpomatic Robur. URL: http:// www.topomatic.ru.
5. Нефедов П.П., Лопухов А.Е. Современный способ решения задачи распределения земляных масс // Транспортное строительство. 1964. № 4.
6. Михалевич В.С., Шор Н.З. Математические основы решения задачи выбора оптимального очертания продольного профиля // Труды Всесоюзного НИИ транспортного строительства. 1964. Вып. 51.
7. Использование математических методов оптимизации и ЭВМ при проектировании продольного профиля железных дорог // Труды Всесоюзного НИИ транспортного строительства. Вып. 101. — М: Транспорт. 1977.
8. Карих Ю.С. Оценка существующих методов проектирования продольного профиля. / В сб. трудов ГипродорНИИ № 17. Повышение экономической эффективности капиталовложений в строительство, ремонт и содержание автомобильных дорог. — М.: ГипродорНИИ, 1976.
9. Пархолуп С. Система проектирования транспортных магистралей Trimble Quantm // САПР и графика. 2013. № 3.
10. Вентцель Е.С. Элементы динамического программирования. — М.: Наука, 1964.
11. Кантор И.И. Изыскания и проектирование железных дорог. — М.: ИКЦ «Академкнига», 2003.
12. Struchenkov V.I.  Mathematical Models and Optimization in Line Structure Routing: Survey and Advanced Results // International Journal Communication, Network and System Sciences. Special Issue : Models and Algorithms for Application. 2012. 5.
13. Струченков В.И. Методы оптимизации в системах автоматизированного проектирования трасс линейных сооружений // САПР и графика. 2013. № 3. 

САПР и графика 7`2013