А не замахнуться ли нам на Габриеля нашего Ламе?

Виктор Чебыкин
Инженер, Новосибирск

Овалы (от фр. ovale — овал) — замкнутые выпуклые плоские кривые. При этом под выпуклостью понимают свойство кривой иметь с любой прямой не более двух (действительных) общих точек [1].

На рис. 1 изображены шесть овальных кривых, на первый взгляд очень похожих между собой (за исключением 1е).

Эллипс

Эту кривую (рис. 1а) знают практически все — это эллипс. Первые упоминания о нем датируются несколькими веками до н.э. Главные свойства эллипса: кривая имеет два фокуса; все лучи, исходящие из одного фокуса, отражаясь от кривой, собираются во втором фокусе и наоборот; сумма отрезков от любой точки кривой до фокусов есть величина постоянная. Значение эллипса трудно переоценить — его геометрия и свойства используются как природой, так и человеком.

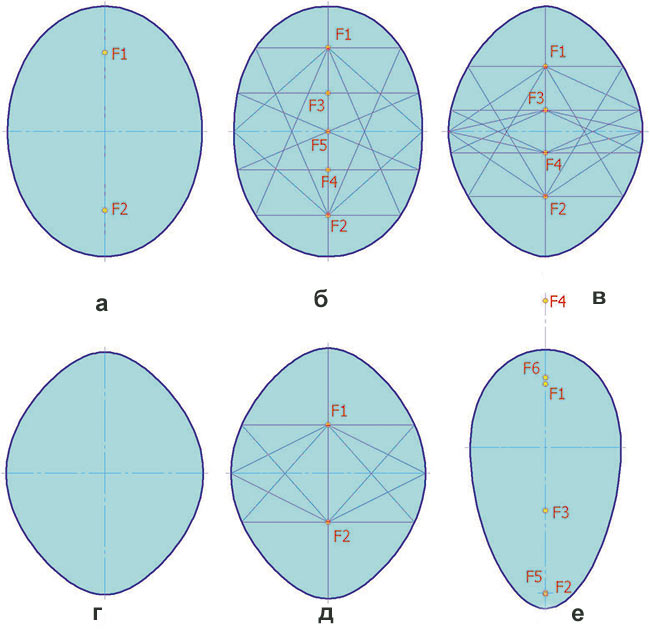
Рис. 1. Овальные кривые: а — эллипс; б — овал Кассини; в — кривая Ламе; г — кривая R-0; д — кривая R-1; е — кривая R-2

Овал Кассини

Еще одну кривую (рис. 1б) предложил астроном Джованни Кассини в XVII веке. Он полагал, что именно по такой траектории движутся планеты Солнечной системы, в чем, как выяснилось, заблуждался.

Овал Кассини — геометрическое место точек, произведение расстояний от которых до фокусов постоянно. Свойства кривой: овал Кассини не всегда имеет эллипсовидную форму и может трансформироваться в точки, совпадающие с фокусами; в два яйцевидных овала; в лемнискату; в окружность… Свойства кривой в диапазоне овалов: наличие двух основных фокусов F1 и F2, а также трех дополнительных фокусов F3, F4, F5, один из которых совпадает с  центром кривой. Две пары лучей, исходящих из фокусов F3 и F4, отраженных от кривой, проходят через центр F5, и после второго отражения от кривой попадают в противоположные фокусы. Таких дополнительных фокусов больше нет ни у одной из описываемых в статье кривых.

Овалы Кассини используются в теории упругости, в конструкциях антенн; установлено геометрическое подобие овалов с формой силовых линий некоторых электромагнитных полей.

Кривая Ламе

Кривая Ламе (рис. 1в) предложена Габриелем Ламе в XIX веке.

Формула кривой:

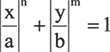 ,    (1)

Формула на вид проста, но при изменении параметров кривая может кардинально менять свою форму (рассматриваем только эллипсовидные формы овала). В отличие от овала Кассини, кривая всегда непрерывна. Еще одно свойство кривой: при разных сочетаниях m, n, a, b она может иметь два либо четыре фокуса или не иметь их вообще. Это свойство наблюдалось в диапазоне значений степеней n и m от 1,5 до 2.

Кривая Ламе (суперэллипс) используется в архитектуре (стадион в Мехико), в дорожном строительстве (площадь с фонтаном в Стокгольме), в дизайне мебели и др.

Следующие три овальные кривые не входят в линейку известных, но, поскольку имеют явное практическое значение (применение) и ряд собственных характерных свойств, также заслуживают упоминания (кривая R­0) или описания и сравнения с известными (кривые R­1 и R­2). Геометрия кривых определена с помощью трехмерных сборок обечайка — люк, выполненных в КОМПАС­3D.

Кривая R­0

Овальная кривая R­0 (рис. 1г) получена в результате разворачивания на плоскость фигуры пересечения круглого цилиндрического люка с круглой цилиндрической обечайкой резервуара при S ® 0, где S — толщина стенки обечайки, определяющая геометрию отверстия. Люк установлен перпендикулярно продольной оси резервуара без смещения. Поскольку  применимость ее незначительна, ограничимся лишь определением: плоская гладкая замкнутая эллипсовидная бесфокусная овальная кривая. 

Кривая R­1

Кривая R­1 (резервуарный овал 1­го рода) (рис. 1д и рис. 2) предложена и описана впервые в статье [2].

Кривая R­1 — это плоская гладкая замкнутая эллипсовидная двухфокусная овальная кривая. Кривая получена в результате разворачивания на плоскость фигуры пересечения круглого цилиндрического люка (патрубка) с круглой цилиндрической обечайкой толщиной S -> 0 с учетом гарантированного зазора D и определяет геометрию отверстия в обечайке. Люк установлен перпендикулярно продольной оси резервуара без смещения от нее.

Следует обратить внимание на большую схожесть кривой R­1 с кривой Ламе (рис. 1в). Эта схожесть не случайна. Автор пытался подогнать кривую Ламе к кривой R­1 методом последовательного приближения. Попытка не удалась — кривые не сходились, кроме того, имели разное  количество фокусов. Вывод — кривая R­1 не является частным случаем кривой Ламе.

Одним из важных свойств овальных кривых R­1 является наличие двух (и только двух) фокусов во всем возможном диапазоне сочетаний параметров: диаметр обечайки, диаметр люка, толщина обечайки, гарантированный зазор. «Гуттаперчевая» кривая Ламе таким свойством не обладает, обращаясь с фокусами более вольно.

Фокусы кривой R­1 могут обменяться между собой восемью парами лучей, отраженных от кривой, и парой прямых лучей. У эллипса, как известно, все лучи от одного фокуса собираются в противоположном.

Овал R­1 обладает еще одним свойством: вышеупомянутые  лучи делят кривую овала на восемь частей. Точки падения этих лучей на кривую являются характерными точками, в которых меняется знак роста суммы пары отрезков от точки кривой до фокусов на противоположный (см. рис. 2). Интервалы кривой с положительными и отрицательными знаками чередуются. У эллипса, как известно, сумма отрезков от любой точки контура до фокусов есть величина постоянная.

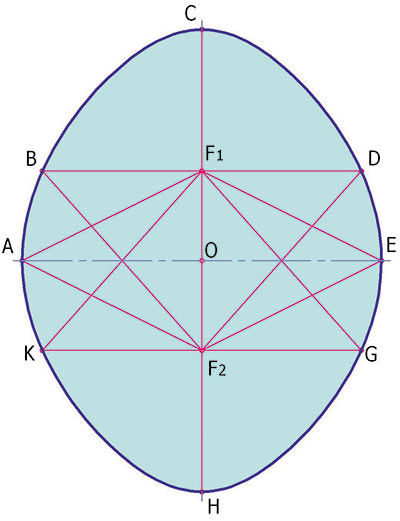
Рис. 2. Овальная кривая R-1

Приведеные здесь формулы* служат для определения большой и малой осей этой овальной кривой:

;   (2)

Xсмз = d + 2△,   (3)

где: Yсмз — большая ось овала (смз  здесь и далее — соединение с минимальными зазорами);

Rвн — внутренний радиус обечайки резервуара;

S — толщина стенки обечайки резервуара;

d — наружный диаметр люка;

△ — гарантированный зазор между обечайкой и люком в любой точке сопряжения (периметральный зазор);

Xсмз — малая ось овала.

Кривая R­2

Кривая R­2 (резервуарный овал 2­го рода) (рис. 1е, рис. 3 и 4) предложена и описана в статье [2].

Кривая R­2 —это плоская  замкнутая яйцевидная шестифокусная овальная кривая. Кривая получена в результате разворачивания на плоскость фигуры пересечения круглого цилиндрического люка (патрубка) с круглой цилиндрической обечайкой резервуара с толщиной стенки S>0 с учетом гарантированного зазора △ и определяет геометрию отверстия в обечайке. Ось люка перпендикулярна продольной оси резервуара. Люк установлен со смещением от этой оси.

Овал R­2 имеет яйцевидную форму. Характерным свойством овала R­2 является наличие шести фокусов (см. рис. 3).

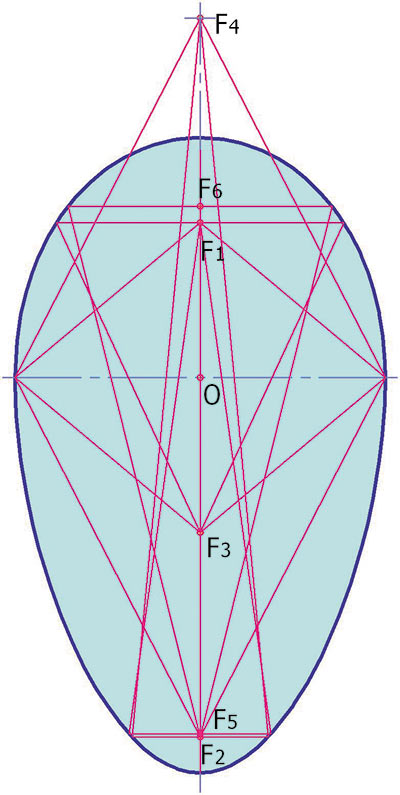
Рис. 3. Овальная кривая R-2

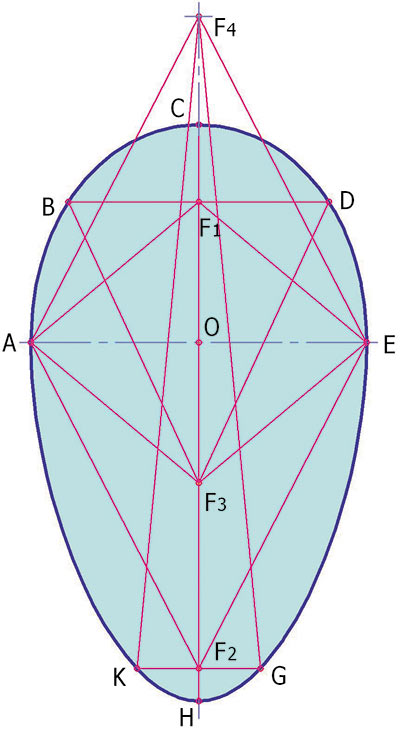
Рис. 4. Овальная кривая R-2. Характерные точки

Рис. 5. Резервуар

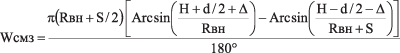(4)

Xсмз = d + 2△,   (5)

Шесть лучей, выпущенные из фокуса F1, отраженные от кривой, собираются в противоположном ему фокусе F3 и, наоборот, фокусы F2 и F4 связаны между собой пятью парами отраженных лучей, пары фокусов F1­F5 и F2­F6 могут обменяться между собой только четырьмя парами отраженных лучей.

Сумма отрезков, соединяющих точки на кривой с фокусами F1 и F2, непостоянна и растет по мере отдаления от полюса H и приближения к полюсу C (см. рис. 4). Сумма отрезков, соединяющих точки на кривой с фокусами F1 и F3, непостоянна и имеет смену знака роста в характерных точках A, B, С, D, E, H. Сумма отрезков, соединяющих точки на кривой с фокусами F2  и F4, также непостоянна и имеет смену знака роста в точках A, C, E, G, H, K.

Еще одно свойство: точки A  и E являются точками перелома кривой, в связи с чем кривая не относится к гладким.

Этими свойствами кривая отличается как от R­1, так и от эллипса.

Размеры осей овальной кривой R­2 можно определить по формулам (4) и (5),где: Wсмз — большая ось овала;

Xсмз — малая ось овала;

H — смещение оси люка от продольной оси резервуара.

Проверка геометрии полученных кривых в 3D­моделлере: на 3D­модели обечайки в развернутом состоянии вырезали по полученной кривой отверстие, после чего обечайку сворачивали в круговой цилиндр и соединяли с моделью люка. Далее с этой 3D­сборки создавался чертеж — вид сверху, на котором проводились измерения. Результат проверки следующий: отклонение от заданного гарантированного зазора не превышало нескольких сотых миллиметра (кривая была выполнена сплайном по 40 точкам). При увеличении количества опорных точек точность построения возрастает.

Кривые проверены непосредственно при разработке и изготовлении резервуаров и показали свою состоятельность. С использованием овальных кривых R­1 и R­2 изготовлено уже несколько сотен резервуаров, при этом ни одного случая плохой стыковки обечайки с люком не зафиксировано, что окончательно доказывает правильность их геометрии.

На рис. 5 показан один из резервуаров, конструкция которого выполнена с использованием кривой R­1.

Выводы

Все описанные в статье овальные кривые, благодаря своим оригинальным свойствам и геометрии, имеют практическое применение, иногда отличающееся от первоначально задуманного (овал Кассини).

Расширена линейка известных овальных кривых. Предложены и описаны «резервуарные» овалы 1­го и 2­го рода (овальные кривые R­1 и R­2), назначение которых определяется объединяющим их термином. 

Библиографический список

1. Большая Советская Энциклопедия. М.: Советская Энциклопедия, 1969­1978.
2. Чебыкин В.Г. Врезка люков в обечайки резервуаров, соединения с минимальными (гарантированными) зазорами. Новые виды овальных кривых — «резервуарные» овалы // Справочник. Инженерный журнал. 2012. № 11. С. 31­33.

САПР и графика 8`2013