Численное моделирование звукового удара в программном комплексе ANSYS CFX

Валерий Вождаев
К.т.н., ведущий научный сотрудник ЦАГИ им. проф. Н.Е. Жуковского.

Леонид Теперин
К.т.н., начальник отдела ЦАГИ им. проф. Н.Е. Жуковского.

В статье исследуется методика расчета звукового удара на местности, индуцированного сверхзвуковым пассажирским самолетом. Выполнено сравнение результатов, полученных с применением программного комплекса ANSYS CFX, с экспериментальными данными. Для оперативного использования промышленного кода ANSYS CFX был разработан макрос, органично включенный в программный интерфейс, что позволило значительно упростить процедуру расчета звукового удара.

Одной из основных задач, которую приходится решать проектировщикам самолетов сверхзвуковой пассажирской авиации, — это минимизация интенсивности волны звукового удара, неизбежно сопровождающей сверхзвуковой полет. Основой для проектирования сверхзвукового летательного аппарата с пониженной интенсивностью звукового удара является прямой расчет эпюры звуковой волны на местности при заданном режиме полета (высота, скорость) и геометрических параметрах самолета.

Методика расчета звукового удара [1] включает решение двух задач: задачи определения ближнего поля около компоновки самолета и задачи распространения звуковой волны в атмосфере до поверхности Земли. Для решения задачи обтекания представляет интерес рассмотрение возможности использования наиболее точных уравнений, которые снимают какие­либо ограничения на форму обтекаемого тела, режимы течения (отрывные или дозвуковые зоны) и позволяют моделировать работу реального двигателя. Основной целью данной работы является разработка методики расчета звукового удара на основе решения осредненных по Рейнольдсу уравнений Навье — Стокса. В качестве системы, реализующей решение осредненных по Рейнольдсу уравнений Навье — Стокса, использовался программный комплекс ANSYS CFX [2] (лицензионное соглашение ЦАГИ № 501024), который был адаптирован к расчету звукового удара и апробирован на тестовых примерах [3].

Современные программные комплексы, базирующиеся на принципах параллельных вычислений уравнений Навье — Стокса, имеют комплексную модульную структуру и помимо основного решающего модуля включают целый ряд программных средств, позволяющих эффективно выполнять вычислительные эксперименты по обтеканию тела сложной конфигурации потоком газа или жидкости. Основные принципы работы современных программных комплексов вычислительной гидродинамики, таких как ANSYS CFX и ANSYS Fluent, показаны на рис. 1.

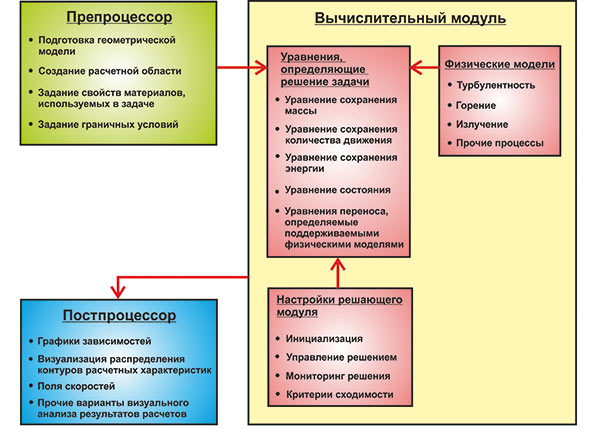
Рис. 1. Схема взаимодействия треx основных модулей, входящих в состав современных комплексов вычислительной газовой динамики

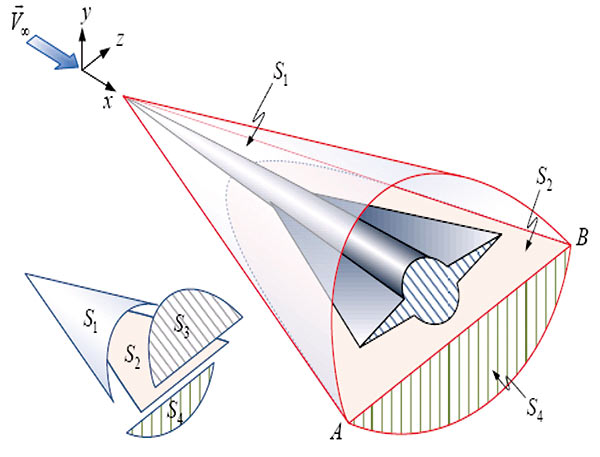
Рис. 2. Контрольный объем при сверхзвуковом обтекании
летательного аппарата

При расчете звукового удара, то есть при определении возмущений на поверхности Земли, создаваемых пролетающим со сверхзвуковой скоростью летательным аппаратом, трехмерное поле течения может быть разделено на две зоны:

• зона 1 с характерным размером r порядка длины тела L (r~L);
• зона 2 с характерным размером порядка R высоты полета H (R~Н).

Обычно Н>>L (например, если высота равна 15 000 м, а длина самолета 50 м, то Н/L=300).

В описанной постановке надо решить две задачи: одна из них формирует начальные данные в трехмерном течении, а вторая рассчитывает распространение возмущения от тела до поверхности Земли.

На первом этапе необходимо рассчитать обтекание компоновки самолета и найти параметры потока вокруг нее (рис. 2). Поверхность S1 является границей возмущенного и невозмущенного потока (конус Маха), плоскость S2, параллельная скорости набегающего потока, находится под телом, но не касается его. Плоскости S3 и S4 определяются огибающими обратных конусов Маха, исходящих из отрезка АB.

Специально для программного комплекса ANSYS CFX был разработан макрос (рис. 3), который на основе методики [3] позволяет рассчитать эпюру звукового удара на местности по данным расчета ближнего поля. Макрос был интегрирован в постпроцессор CFX­Post.

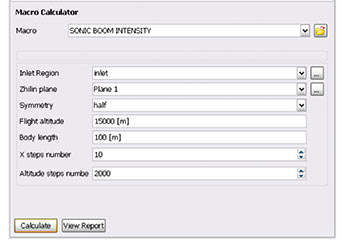
Рис. 3. Интерфейс макроса для расчета звукового удара
в среде ANSYS CFX

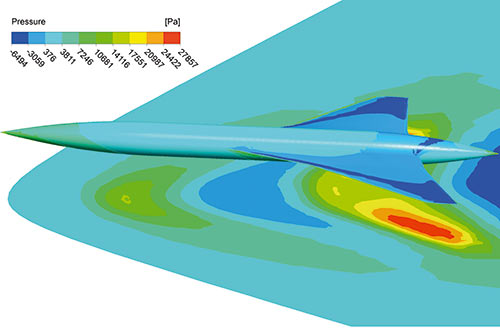
Рис. 4. Результаты расчета характеристик обтекания компоновки летательного аппарата в CFX-Post

После того как решена задача обтекания компоновки летательного аппарата, для расчета интенсивности звукового удара прежде всего необходимо в постпроцессоре CFX создать плоскость, параллельную набегающему потоку, которая будет располагаться под летательным аппаратом в непосредственной близости от него, но его не касаться (рис. 4). Эта плоскость на рис. 2 соответствует плоскости S2. Применение данного метода определения звукового удара на местности требует точного расчета распределения давления в плоскости S2. Это предъявляет высокие требования к качеству расчетной сетки. При ее подготовке необходимо применять локальное измельчение в области между летательным аппаратом (ЛА) и плоскостью S2.

Для работы макроса необходимо задать следующие параметры:

• Inlet Region — граничная поверхность, через которую поток входит в расчетную область;
• Zhilin Plane — плоскость S2;
• Symmetry — параметр, определяющий, используется полная модель (full) или ее симметричная половина (half);
• Flight altitude — высота полета ЛА;
• Body length — характерная длина ЛА;
• X steps number — число шагов вдоль продольной оси;
• Altitude steps number — число шагов по высоте.

Два последних параметра определяют степень дискретизации пространства. Установленные по умолчанию значения (500 и 2000 соответственно) позволяют получить решение с достаточно высокой степенью точности. Увеличение числа шагов вдоль продольной оси требует больших затрат оперативной памяти и может привести к сбоям в работе программы.

Рис. 5. Самолет Ту-144: а — вид сзади; б —линии тока
на поверхности расчетной модели и форма струй сопла

Аспирантом МФТИ Чо Кю Чулом был выполнен комплекс тестовых расчетов для самолета Ty­144 (рис. 5а). Расчеты были сделаны с помощью программного комплекса CFX и разработанного макроса. При моделировании силовой установки Ту­144 необходимо учитывать также влияние струй двигателей на поле возмущения плоскости S2 и эпюру звукового удара. На рис. 6а показаны форма и положение силовой установки, использованные в данной работе. Направление и угол раствора сопла показаны на рис. 6б. Направление струи θcd изменяется с углом атаки, а угол сопла (θc) предполагается равным оптимальному значению — 10.

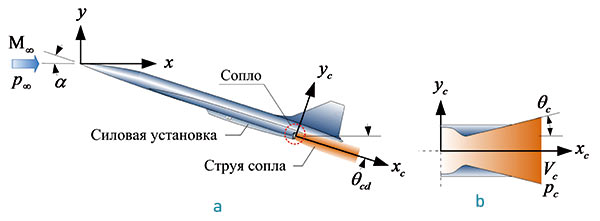
Рис. 6. Самолет с силовой установкой:
а — схема истечения струи; б — сопло

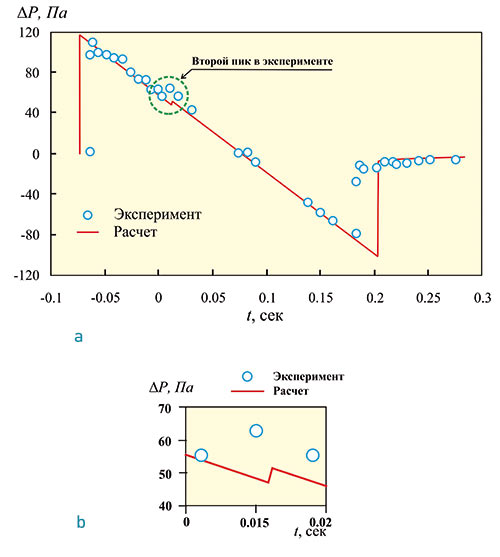
Рис. 7. Влияние струи двигателя на эпюру звукового удара самолета Ту-144: а — эпюра избыточного давления в N-образной волне, б — второй пик в эксперименте

Результаты расчетов в сравнении с экспериментальными данными [4] показаны на рис. 7. Учет струй двигателя создает второй пик в эпюре избыточного давления (рис. 7а). В эксперименте эпюра избыточного давления звуковой волны самолета Ту­144 имеет также второй пик, более интенсивный (рис. 7б), что может быть результатом влияния струй сопла, работающих при углах истечения потока из сопла, которые не были зафиксированы при проведении эксперимента. Рис. 5б иллюстрирует характер обтекания самолета Ту­144 с работающими двигателями при расчетных параметрах истечения струи.

Созданный макрос, применимый для любой версии ANSYS CFX и органично включенный в алгоритм этого промышленного кода, который был взят в качестве инструмента определения ближнего поля по уравнениям Навье — Стокса, позволил разработать эффективную процедуру расчета звукового удара на местности.

Литература

1. Жилин Ю.Л., Коваленко В.В. О связывании ближнего и дальнего полей в задаче о звуковом ударе // Ученые записки ЦАГИ, т. ХХIX. 1998. № 3 и 4. C. 111­122.
2. Menter F.R., Galpin P.F., Esch T.,
   Kuntz M., Berner C. CFD Simulations of Aerodynamic Flows with a Pressure­Based Method // Paper ICAS 2004­2.4.1. Japan, Yokohama, 2004. 11 p.
3. Вождаев В.В., Коваленко В.В., Теперин Л.Л., Чернышев С.Л. Методика определения интенсивности звукового удара на местности при исследовании компоновки сверхзвукового пассажирского самолета // Полет. 2013. № 10. C. 17­27.
4. Завершнев Ю.А., Роднов А.В. Летные испытания сверхзвуковых пассажирских самолетов первого поколения по звуковому удару // Международная научно­техническая конференция «Новые рубежи авиационной науки» ASTEC’07, Москва, 19­22 августа 2007 г. 

САПР и графика 1`2014