Имитационная модель образования усадочной раковины и макропористости

Валерий Монастырский
K.т.н., доцент МГМУ «МАМИ»
Михаил Ершов
Д.т.н., проф., зав. кафедрой «Машины и технологии литейного производства» МГМУ «МАМИ»

Введение

Компьютерное моделирование литейных процессов — эффективное средство сокращения затрат времени и ресурсов при освоении производства литых заготовок. Главная задача, возникающая при разработке технологического процесса (получение плотной отливки), решается на основе прогноза пористости, получаемого в результате моделирования.

Физическая схематизация и математическая модель образования макропористости и усадочной раковины представлены в работах [1, 2]. Согласно этой модели, формирование усадочной раковины рассматривается как процесс течения расплава под действием разности давлений, возникающей в двухфазной зоне отливки при кристаллизации. Образование замкнутой усадочной раковины и макропористости происходит как процесс создания новых поверхностей раздела, то есть из­за нарушения сплошности расплава под действием растягивающих напряжений, превышающих предел его прочности [3].

Основные трудности при моделировании процесса затвердевания отливки связаны с определением постоянно меняющейся границы металла и окружающей среды (открытой усадочной раковины) и с возникновением новых поверхностей раздела внутри металла: макропористости и закрытой усадочной раковины. Существующие методы построения произвольной свободной поверхности движущейся жидкости, такие как front­tracking, адаптивные сетки и volume­of­fluid (VOF), обеспечивают высокую точность определения криволинейной поверхности расплава, но сложны в реализации и требуют больших вычислительных ресурсов, поэтому чаще используются в научных целях [4].

Для решения практических задач литейного производства широко применяется имитационная модель на основе пошагового метода и баланса массы отливки, в которой единый физический процесс течения расплава под действием сил, возникающих в результате его кристаллизации, расщеплен на несколько процессов, протекающих независимо друг от друга. Имитационная модель значительно проще в реализации и достаточно адекватна. Многолетний опыт применения такой модели в составе СКМ ЛП «ПолигонСофт» [5] показывает, что при правильном выборе параметров модели прогноз пористости в отливке практически всегда подтверждается экспериментом.

Ранее был предложен [6] метод пошагового определения формы усадочной раковины с учетом капиллярного питания междендритных пространств над свободной поверхностью расплава применительно к конечно­разностной модели отливки. Эта статья посвящена разработке численной модели, имитирующей процессы формирования усадочной пористости с учетом капиллярных сил, возникающих в двухфазной зоне кристаллизующейся отливки на конечно­элементной сетке и реализации ее в составе СКМ ЛП «ПолигонСофт».

Общие положения модели пористости

Образование усадочной пористости происходит в присутствии формирующегося каркаса твердой фазы. Размеры междендритных пространств определяют капиллярные силы, действующие в двухфазной зоне. Поскольку величина этих сил может превосходить металлостатическое давление и давление окружающей среды, можно предположить, что в формировании внутренних усадочных раковин и макропористости капиллярные силы играют важную роль. Учет капиллярных сил позволяет сформулировать модель, в которой образование макропористости зависит от дисперсности дендритного каркаса, что делает модель более адекватной и открывает возможности для прогнозирования размеров пор.

Рассмотрим процесс кристаллизации расплава, залитого в форму, остывание которого происходит вследствие отвода тепла в окружающую среду как через стенки формы, так и непосредственно со свободной поверхности расплава. Отливка, представленная своей сеточной моделью, разбита на элементарные объемы — тетраэдры с узлами, расположенными в их вершинах. Данная сеточная модель используется для решения тепловой задачи — расчета распределения температуры в литейном блоке методом конечных элементов.

Будем полагать, что температура в элементарных объемах, ассоциированных с узлом i сетки, известна из решения соответствующего уравнения теплопроводности. Будем считать также, что свободная поверхность расплава (зеркало) является плоской и в начальный момент времени находится на верхней границе отливки. Фазовый состав металла в элементарном объеме характеризуется равновесными объемными долями жидкой fL и твердой fs фаз, расчет которых по химическому составу сплава и известной температуре может быть сделан с помощью одной из известных термодинамических баз данных.

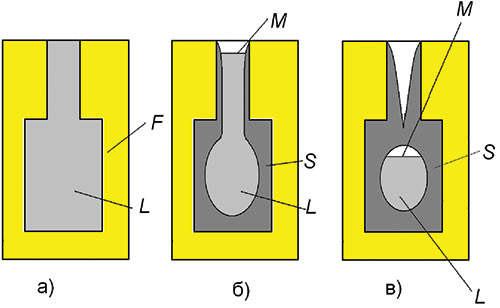
Рис. 1. Схематическое изображение этапов затвердевания отливки: М — зеркало расплава; L — расплав; S — твердая фаза; F — форма; а — исходное состояние; б — образование усадочной раковины; в — кристаллизация замкнутого объема расплава в тепловом узле с образованием внутренней усадочной раковины или рассеянной пористости

Следуя принятым модельным представлениям, будем считать, что, если доля жидкой фазы удовлетворяет условию fL > fL**, твердая фаза не образует неподвижного дендритного каркаса и перемещается вместе с зеркалом расплава [1, 5, 6]. С момента образования жесткого дендритного каркаса fL > fL** движение твердой фазы становится невозможным.

В общем виде процесс кристаллизации отливки проходит следующие стадии: формирование усадочной раковины при кристаллизации открытого теплового узла, образование замкнутого теплового узла, а также внутренней усадочной раковины или рассеянной пористости (рис. 1).

Тепловой узел считается открытым, если расплав находится в контакте с окружающей средой (рис. 1б). В том случае, если непосредственного контакта расплава с окружающей средой нет, тепловой узел считается закрытым (рис. 1в)

Базируясь на представленной на рис. 1 последовательности кристаллизации отливки, рассмотрим математические модели формирования усадочных дефектов на каждом из этапов.

Кристаллизация открытого теплового узла

Кристаллизация расплава сопровождается усадкой металла. В открытом тепловом узле кристаллизация не приводит к падению давления, если усадка компенсируется опусканием свободной поверхности или зеркала расплава. Поверхность расплава является свободной и способна перемещаться, если на ней нет неподвижного каркаса твердой фазы, то есть fL > fL** (рис. 2).

Опускание зеркала расплава должно компенсировать усадку металла на данном временном шаге. Перемещение зеркала определяется выражением: ΔY = VΩ /SM , где VΩ— объем усадки, SM — площадь зеркала расплава.

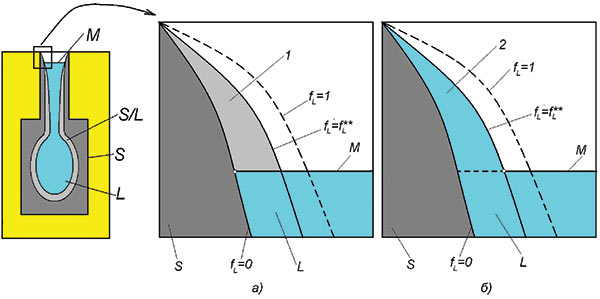
Рис. 2. Схема кристаллизации открытого теплового узла при наличии зеркала расплава: а — модель СКМ ЛП «ПолигонСофт»; б — предлагаемая модель; 1 — зона осушенных дендритов; 2 — зона, питаемая расплавом за счет капиллярного эффекта; S/L — зона непрерывного дендритного каркаса, fL ≤ fL**

Объем усадки на данном временном шаге равен 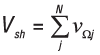, где VΩj — объем усадки в узле конечно­элементной сетки; N — число узлов в пределах теплового узла (далее — в пределах зоны).

По условиям модели, в расположенных выше зеркала узлах сетки, в которых нет неподвижного дендритного каркаса, то есть fL > fL**, металла быть не должно, таким образом, фактические доли жидкой gL и твердой фазы gs должны быть равны 0, а доля пор — gp –1.

Объем отливки, приписываемый к каждому узлу конечно­элементной сетки, равен одной четвертой суммы объемов элементов, к которым принадлежит данный узел. Таким образом, опускание зеркала ниже данного узла отливки приводит к исключению из расчета металла, объем которого Vm может быть больше усадки Vsh. Ошибка, вносимая такой операцией в расчет массы отливки, возрастает с увеличением размера элементов конечно­элементной сетки. Для устранения этой ошибки и сохранения постоянства массы отливки в модели принято пропорциональное уменьшение объемов металла в узлах над зеркалом расплава в соответствии с выражением φVm = Vsh, где fφ— коэффициент пропорциональности. Доля жидкой и твердой фаз в узлах, оказавшихся над зеркалом расплава, уменьшается в соответствии с выражением: g' = (1 – φ) g, где g, g’ — доля фазы в начале и конце шага по времени соответственно.

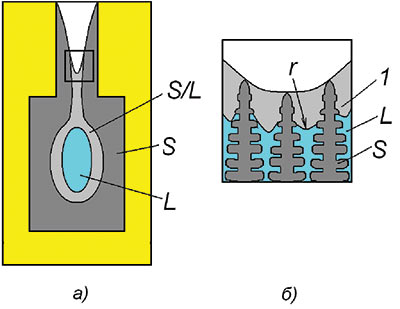
Рис. 3. Схема образования макропористости в двухфазной зоне на границе открытого теплового узла: L — расплав; S — твердая фаза; F — форма; 1 — зона осушенных дендритов (макропористость); r — радиус кривизны поверхности расплава; S/L — зона непрерывного дендритного каркаса, fL ≤ fL**

На рис. 2 схематически показан принцип взаимодействия двухфазной зоны отливки с зеркалом расплава, реализованный в модели макропористости СКМ ЛП «ПолигонСофт» и в модели, предлагаемой в данной работе. В модели СКМ ЛП «ПолигонСофт» перемещение зеркала расплава в неподвижном дендритном каркасе приводит к осушению междендритных пространств и образованию макропористости (рис. 2а, зона 1), объемная доля которой численно равна fL [7].

В настоящей модели предполагается, что дендритный каркас над уровнем расплава полностью заполнен расплавом за счет капиллярного эффекта. В зоне капиллярного питания gL = fL  и gs = fs (рис. 2б, зона 2). В зоне fL ≤ fL** свободной поверхности расплава не существует.

Образование непрерывного дендритного каркаса (зоны, где fL ≤ fL**) вокруг расплава затрудняет контакт расплава с окружающей средой (рис. 3а). Свободная поверхность расплава, оказавшись в дендритном каркасе, теряет способность свободно перемещаться. Из­за влияния капиллярных сил, действующих в дендритном каркасе, усадка металла при кристаллизации лишь частично компенсируется изменением уровня расплава, что приводит к понижению давления в тепловом узле. Распределение давления определяется выражением:

P = Patm + pLgh – E(VΩ – VP)|VL,                                                         (1)

где Patm — внешнее давление на момент образования теплового узла, h — высота столба расплава от наивысшей точки в тепловом узле,
где fL ≥ fL** ; E  — модуль сжимаемости расплава; VΩ — объем усадки, возникшей в тепловом узле на данном временном шаге; VP — объем пористости, возникшей на данном временном шаге из­за изменения уровня расплава; VL — объем расплава в тепловом узле.

Из­за возникшего разрежения расплав втягивается в центр теплового узла, осушая междендритные пространства на его периферии, что приводит к образованию макропористости (зона Р на рис. 3б). Падение давления в тепловом узле и объем образовавшейся пористости зависят от капиллярных сил, действующих в дендритном каркасе. Условно выражение, определяющее равновесие между силами, втягивающими расплав с периферии в центр теплового узла, и капиллярными силами, препятствующими этому процессу, может быть записано в следующем виде:

2σ/r = E(VΩ – VP)|VL.                                                                           (2)

Здесь r — радиус кривизны менисков в междендритных пространствах. Для оценки r используется выражение r = lIIÖ fL, где lII — расстояние между вторичными осями дендритов. Уравнение (2) позволяет определить величину VP и назначить пористость в пограничных узлах конечно­элементной сетки.

Образование раковины в замкнутом тепловом узле

С некоторого момента из­за уменьшения доли жидкой фазы границы теплового узла становятся непроницаемыми, усадка металла при кристаллизации более не компенсируется изменением уровня расплава в дендритном каркасе и тепловой узел становится замкнутым (рис. 4). Это приводит к интенсивному понижению давления в тепловом узле, которое определяется следующим выражением:

P = Patm + pLgh – EVΩ|VL.                                                    (3)

Последний член в выражении (3) определяет падение давления из­за усадки. По истечении некоторого времени, когда давление в какой­либо точке теплового узла падает до критического значения Pcrit, становится энергетически выгодным образование нового зеркала расплава в зоне свободного расплава (fL ≥ fL**). Следует отметить, что для образования новой поверхности раздела требуется выполнение некоторой работы, поэтому Pcrit < 0 [3, 8].

Возникновение новой плоской поверхности раздела полностью компенсирует усадку, накопившуюся в тепловом узле с момента его изоляции. Поэтому местонахождение зеркала расплава может быть определено из условия равенства образовавшейся раковины объему усадки: VP = VΩ.

С появлением зеркала расплава тепловой узел вновь становится открытым в том смысле, что кристаллизационная усадка впредь будет компенсироваться опусканием зеркала расплава. В узле будет формироваться усадочная раковина по алгоритму, описанному выше (см. рис. 2).

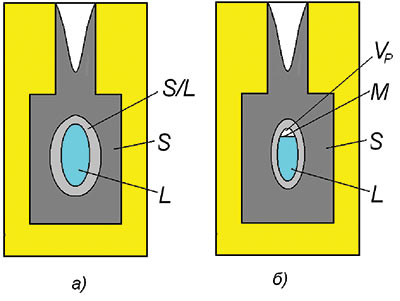
Рис. 4. Схема образования усадочной раковины (б) в закрытом тепловом узле (а): L — расплав; S — твердая фаза; F — форма; М — зеркало расплава; VP — объем усадочной раковины

Образование макропористости в замкнутом тепловом узле

Если в замкнутом тепловом узле повсеместно существует неподвижный каркас твердой фазы, то есть везде fL ≤ fL**, образование плоской свободной поверхности расплава невозможно.

Нарушение сплошности расплава из­за падения давления происходит путем образования макропористости. Первая пора возникает при падении давления ниже критической величины Pcrit < 0. Наиболее вероятным местом зарождения поры является точка, в которой давление минимально, то есть движущая сила образования поверхности раздела
Φпис(P; Pcrit) = Pcrit – P >0 является наибольшей.

После того как в зоне начался процесс образования пор, усадка, возникающая на следующем временном шаге, вероятнее всего, будет компенсироваться ростом уже существующих пор. Условием этого процесса является P ^{k + 1} < – Pσk в тех узлах конечно­элементной сетки, где имеется пористость. Здесь k — номер шага по времени. Движущая сила этого процесса характеризуется функцией: Φporo(P; Pσt) = –Pσt – P.

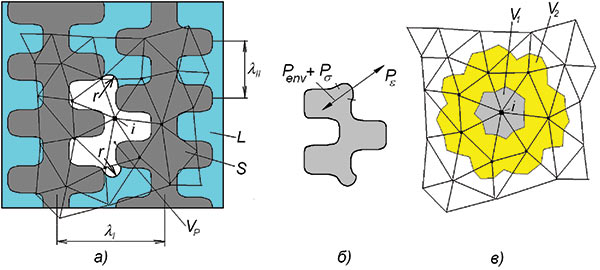
Рис. 5. Образование макропористости в закрытом тепловом узле:
а — схема образования поры в неподвижном дендритном каркасе;
б — силы, действующие на поверхности раздела пора-расплав;
в —распределение пористости в узлах КЭ. L — расплав; S — твердая фаза; VP — пора; r — радиус кривизны мениска; λI ,λII — расстояния между первичными и  вторичными осями дендритов

По мере кристаллизации расплава уменьшается радиус каналов в каркасе твердой фазы, растет капиллярное давление на границе поры и, соответственно, уменьшается давление в расплаве, которое способно обеспечить рост поры (рис. 5). В том случае, когда давление, необходимое для роста существующей поры, оказывается ниже Pcrit, более вероятным становится образование новой зоны пористости. Соотношение Φporo и Φпис определяет, какой из процессов — создание новой зоны пористости или развитие уже существующей — будет преобладать. При Φporo ≥ Φпис будет развиваться существующая зона пористости, при
Φпис > Φporo — образовываться новая.

Рис. 5 иллюстрирует алгоритм моделирования зарождения поры в дендритном каркасе.

Образовавшаяся в узле i пора первоначально занимает объем V1, приписанный к этому узлу. Если этот объем меньше объема усадки, который следует компенсировать, происходит «рост» поры за счет соседних узлов КЭ­сетки с суммарным объемом V2 и т.д. (рис. 5в). Рост поры прекращается, когда отрицательное давление в тепловом узле уравновешивается капиллярными силами. 

Penv + Pσ = Pε,                                                                      (4)

где Penv = Patm + pLgh, Patm — атмосферное давление, h — высота столба расплава; Pσ — силы поверхностного натяжения; Pε — падение давления из­за усадки.

На основании (4) баланс давлений для i­го узла на границе раздела расплав — пора может быть записан так:

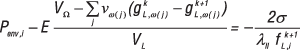,                                               (5)

где gLk, gLk+1 — фактическая доля жидкой фазы в узле до и после образования поры (на временных шагах k и k + 1); vω(j) — объем, ассоциируемый с узлом номер j из списка w. Суммирование ведется по списку узлов ω(j), принявших участие в образовании поры.

Рост зоны пористости идет, пока левая часть уравнения (5) больше правой. Для выполнения этого равенства в левую часть уравнения нужно подключать, кроме суммы по узлам­соседям зародышевого узла i, суммы по соседям этих соседей — ω1, ω2...ωn :

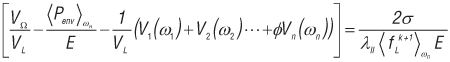.               (6)

Здесь  — средняя величина доли жидкой фазы по набору узлов ω(j). В этих выражениях V1 = gl,ivi — объем усадки, компенсирующейся за счет осушения объема при узле, в котором зарождается пора; V2 — объем усадки, который может быть компенсирован за счет удаления всего расплава из узлов, соседствующих с узлом зарождения поры (из его «звезды»), то есть 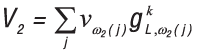. V3 вычисляется для узлов, образующих звезду для узлов, учтенных в V2, и т.д. Коэффициент пропорциональности φ характеризует степень осушения узлов из списка ωn, находящихся на периферии образовавшейся зоны пористости. Решение уравнения баланса (6) позволяет определить узлы, в которых из соображений баланса давлений (4) должна быть назначена пористость.

Ниже приведем одно из возможных решений уравнения (6). Формализуя последовательность распространения поры по узлам КЭ­сетки, запишем:

L0 = VΩ|VL – (Penv) ωn/E, L1 = L0 – V1(ω1)|VL, Ln = Ln­1 – Vn (ωn)| VL , .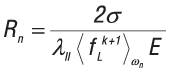

Уравнение (6) принимает вид Ln­1 – φVn (ωn)|VL = Rn, откуда:

φ = (Ln­1 – Rn)VL |Vn(ωn).                       (7)

На основании этого решения назначается пористость gP = gL в узлах из списков ω1,... ωn­1  . В узлах из списка Ωn назначается пористость gP = φ. gL.

Результаты и обсуждение

Представленная в данной статье модель реализована в СКМ ЛП «ПолигонСофт» [5] версии 13.4 для опробования в тестовом режиме.

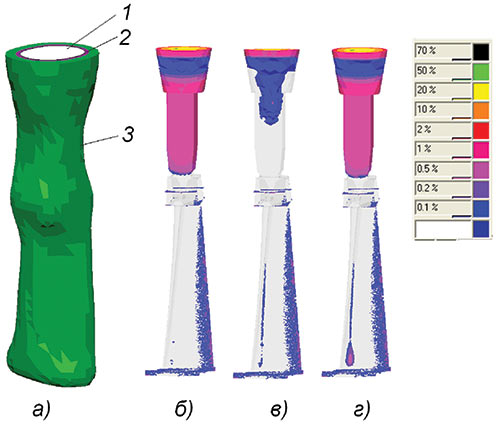
Рис. 6. Результат моделирования пористости в рабочих лопатках
ГТУ СТ-20: а — внешний вид литейного блока; б — Pcrit = –1 МПа,
λII = 30 мкм, Е = 200 МПа; в — Pcrit = –0,1 МПа, λII = 300 мкм, Е = 2000 МПа; г — Pcrit = –0,1 МПа, λII = 30 мкм, Е = 2000 МПа.
1 — отливка; 2 — керамическая оболочка; 3 — теплоизоляция

На рис. 6 представлены результаты моделирования процесса затвердевания крупногабаритной рабочей лопатки ГТУ из сплава ЧС70 по технологии, описанной в работе [9]. Расчеты производились при fL**= 0,7 и различных значениях параметров Pcrit , λII и E, диапазон изменения которых был выбран из следующих соображений. Образование усадочной поры происходит при падении давления в расплаве до критической величины Pcrit. Давление в расплаве в момент образования усадочной поры является отрицательной величиной, порядок которой можно оценить из уравнения Лапласа P = –2σ/r.

Исходя из поверхностного натяжения для расплава никеля σ ≈ 1,7 Нм [10] и диаметра пор, наблюдаемых в данной отливке 3,5­60 мкм, можно предполагать, что давление в расплаве в момент образования поры может составлять от –0,1 до –1 МПа.

Радиус мениска r зависит от размеров междендритных пространств, которые определяются скоростью охлаждения расплава в двухфазной зоне. Полагалось, что при затвердевании отливок подобных размеров возможные междендритные расстояния (между вторичными осями, между первичными осями или между зернами) находятся в диапазоне 20 - 300 мкм.

Модуль сжимаемости расплава может быть оценен по формуле: E = a2pl, где a — скорость звука в расплаве; pl — плотность расплава. Опираясь на известные данные по скорости звука для расплавов чистых металлов, взятые из [10], можно считать, что Е = 3.104 ¸ 105 МПа. Следует учитывать, что в сплавах скорость звука значительно ниже, чем в чистых металлах.

В предлагаемой модели модуль сжимаемости характеризует процесс падения давления в тепловом узле. В идеальных условиях скорость падения давления в замкнутом тепловом узле пропорциональна E. При кристаллизации реальной отливки твердая корка металла, окружающая тепловой узел, может быть негерметичной, что снижает скорость падения давления в узле. Существует также возможность деформации корки под действием разности давлений окружающей среды и внутри теплового узла, что также снижает скорость падения давления, поскольку часть кристаллизационной усадки компенсируется деформацией. Это свидетельствует о том, что эффективный модуль сжимаемости расплава должен быть значительно меньше теоретической оценки. В рамках данной модели перечисленные явления не рассматриваются, и поэтому модуль сжимаемости, как и критическое давление, является настроечным параметром, который должен определяться на основе экспериментальных данных

Как и ожидалось, объемная доля пористости зависит от выбора параметров модели Pcrit  и λII, определяющих момент достижения давления, при котором начинает образовываться пористость. В вариантах, приведенных на рис. 6а и б, пористость в пере лопатки не превышает 0,2%. На рис. 6в пористость в пере достигает 1,5%. Расположение зоны пористости практически не зависит от настроек модели и определяется геометрией отливки и технологией заливки. В целом результаты моделирования вполне согласуются с результатами металлографического исследования отливок и моделирования в стандартной модели СКМ ЛП «ПолигонСофт» [9].

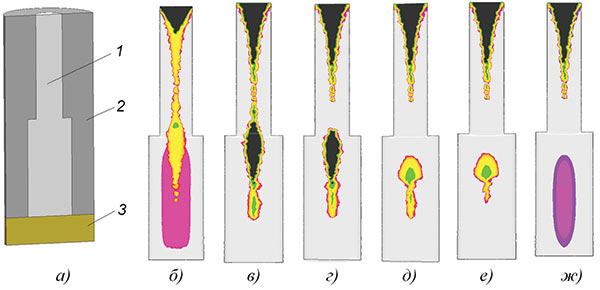
Рис. 7. Результат моделирования пористости в составной отливке из Ст.3:
а — внешний вид литейного блока; 1 — отливка; 2 — металлическая форма из Ст.3; 3 — песок; б — СКМ «Полигон»; в — Pcrit = –1 МПа, λII = 300 мкм, Е = 2000 МПа; г — Pcrit = –20 МПа, λII = 300 мкм, Е = 2000 МПа; д — Pcrit = –20 МПа, λII = 300 мкм, Е = 200 МПа; е — Pcrit = –20 МПа, λII = 10 мкм, Е = 200 МПа; ж — Pcrit = –20 МПа, λII = 1 мкм, Е = 200 МПа

Чтобы оценить чувствительность к параметрам модели Pcrit , λII и E, было также проведено моделирование процесса затвердевания отливок из стали Ст.3. Затвердевание происходило в кокиле из Ст.3 на песчаном основании (рис. 7). Теплофизические свойства отливки были рассчитаны в термодинамической базе данных Computherm [11] по химическому составу сплава. Исходная температура металла была равна 1550 °С, кокиля и песка — 500 °С. Охлаждение происходило в окружающую среду (воздух) с температурой 20 °С конвекцией с коэффициентом теплоотдачи 10 Вт/м2/К и излучением при степени черноты кокиля и металла 0,8.

Для сравнения были проведены расчеты в СКМ Полигон версии 13.3.1 при типовых настройках, применяемых для моделирования в литейном производстве ФГУП НПЦГ «Салют».

Результаты моделирования представлены на рис. 7. Затвердевание отливки во всех представленных вариантах соответствует схеме, приведенной на рис. 1. На первом этапе идет кристаллизация открытого теплового узла с компенсацией усадки за счет перемещения зеркала расплава. На втором этапе происходит образование закрытого теплового узла, в котором, в зависимости от заданных параметров модели, либо образуется закрытая раковина (рис. 7в и г), либо рассеянная макропористость (рис. 7д­ж). Реализация одного из этих вариантов зависит от скорости протекания двух процессов — падения давления в тепловом узле вследствие кристаллизационной усадки и роста доли твердой фазы, приводящего к образованию непрерывного дендритного каркаса.

Быстрое падение давления в тепловом узле до критической величины Pcrit прежде образования непрерывного дендритного каркаса приводит к образованию зеркала расплава и формированию внутренней усадочной раковины. Этому варианту формирования пористости способствует большой модуль сжимаемости E, низкое критическое давление Pcrit и большое значение fL**. Как видно из рис. 7в и г, значение модуля сжимаемости 2000 МПа является достаточно большой величиной, обеспечивающей быстрое падение давления в тепловом узле и образование зеркала расплава при любом критическом давлении (вплоть до –20 МПа). Поэтому задание большего значения E не приводит к изменению прогноза пористости.

При низком модуле сжимаемости давление в тепловом узле падает медленно и достигает критической величины, когда непрерывный каркас твердой фазы уже сформирован. В этом случае накопившаяся кристаллизационная усадка реализуется в виде рассеянной макропористости (рис. 7д и ж). Объемная доля и размер образующихся пор зависят от количества жидкой фазы и параметров дендритного каркаса — расстояния между вторичными осями дендритов. 

Литература

1. Журавлев В.А., Сухих С.М. Машинное моделирование формирования распределенной пористости и усадочной раковины при кристаллизации сплавов в слитки // Известия АН СССР. Металлы. 1981. № 1. C. 80­84.
2. Журавлев В.А., Бакуменко С.П., Сухих С.М. и др. К теории образования замкнутых усадочных полостей при кристаллизации сплавов в больших объемах // Известия АН СССР. Металлы. 1983. №1. С. 43­48.
3. Журавлев В.А. О макроскопической теории кристаллизации сплавов // Известия АН СССР. Металлы. 1975. № 5. C. 93­99.
4. Dawei Sun and Suresh V. Garimella. Numerical and Experimental Investigation of Solidification Shrinkage // Numerical Heat Transfer. Part A. 2007. 52, pp. 145­162.
5. СКМ ЛП «ПолигонСофт», торговая марка ЗАО «СиСофт Девелопмент», http://csdev.ru.
6. Монастырский В.П. Моделирование образования макропористости и усадочной раковины в отливке // Литейщик России. 2011. № 10. C. 16­21.
7. Тихомиров М.Д. Основы моделирования литейных процессов. Усадочная задача. — М.: Приложение к журналу «Литейное производство». 2001. № 12. C. 8­14.
8. Kent D. Carlson, Zhiping Lin, C. Beckermann, G. Mazurkevich, and Marc C. Schneider. Modeling of Porosity Formation in Aluminum Alloys. Proceedings MCWASP­XI, ed. Ch.­A. Gandin, M.Bellet (Warrendale, PA: the Minerals, Metals & Materials Society, 2006), рр. 627­634.
9. Монастырский В.П., Монастырский А.В., Левитан Е.М. Разработка технологии литья крупногабаритных лопаток ГТД для энергетических установок с применением систем «Полигон» и ProCAST//Литейное производство. 2007. № 9. C. 29­34.
10. Физические величины: Справочник / Бабичев А.П., Бабушкина Н.А., Братковский А.М. и др.; Под ред. Григорьева И.С., Мейлихова Е.З. — М.: Энергоатомиздат, 1991. 1232 с.
11. Thermodynamic Database for Iron­Based Superalloys: PanIron 5.0, CompuTerm, LLC, USA.

САПР и графика 3`2014