Использование ANSYS для междисциплинарного моделирования вихретоковых средств измерений в металлургии
Сегодня более 90% стали в мире производится в машинах непрерывного литья заготовок (МНЛЗ). Основным узлом МНЛЗ является кристаллизатор, в состав которого входит медная гильза, открытая с двух сторон. Жидкая сталь непрерывно поступает в гильзу, где металл кристаллизуется. Затем сформировавшийся слиток вытягивают из кристаллизатора. В процессе разливки медная гильза охлаждается водой.
Качество стальной заготовки зависит от точности стабилизации уровня. Сейчас измерение уровня производится с использованием вихретоковых датчиков.
В силу ряда объективных причин зачастую бывает сложно провести исследование датчика в промышленных условиях. Специфика металлургического производства, а именно — наличие высоких температур, не позволяет провести испытания в лабораторных условиях. Поэтому в процессе разработки и исследования наиболее рационально использование инженерного компьютерного анализа на базе программного комплекса ANSYS.
В данной статье приводятся результаты моделирования двух конструкций датчика уровня расплава для сортового кристаллизатора, на основе которых был разработан алгоритм обработки сигнала и определена оптимальная частота возбуждающего тока. Моделирование производилось при поддержке группы компаний «ПЛМ Урал» — «ДелкамУрал».
Для сортового кристаллизатора с малым проходным сечением можно расположить вихретоковый датчик либо в накладном варианте — на рубашке из нержавеющей стали, находящейся снаружи гильзы кристаллизатора, либо в проходном варианте, устанавливая обмотки вокруг рубашки (рис. 1). Накладной ДУМ состоит из одной вытянутой возбуждающей катушки и восьми соосных с ней измерительных катушек. Проходной ДУМ состоит из восьми включенных последовательно параметрических проходных вихретоковых датчиков.
При такой конструкции измерять уровень приходится через медную стенку толщиной 1015 мм, которая является сильным электромагнитным экраном. Температура, а следовательно, и электрическая проводимость медной стенки при перемещении уровня значительно изменяются. Изза экранирования расплава медной стенкой сигнал от стали оказывается слабым. Измерять его уровень возможно только по тепловому распределению в гильзе, максимум которого соответствует уровню расплава. При такой постановке задачи необходимо рассматривать мультифизичную модель (рис. 2).
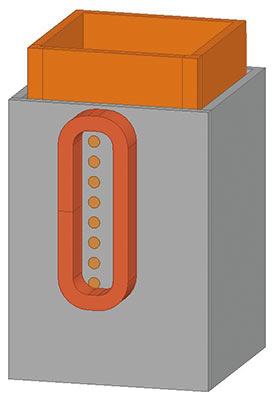
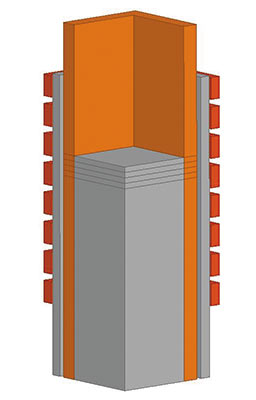
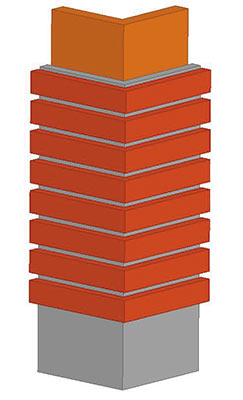
Рис. 1. Модель накладного (слева) и проходного (посередине и справа) датчика уровня расплава
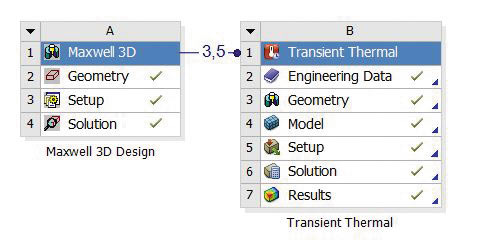
Рис. 2. Междисциплинарный расчет в Workbench
Оба типа датчиков моделировались в трехмерной постановке, причем вследствие симметрии модели проходного датчика была использована четверть геометрии.
Для моделирования электромагнитных процессов применялся модуль Maxwell 16.0, решатель гармонических полей EddyCurrent (рис. 3). Медная гильза и расплав моделировались электроизолированными, поскольку между ними во время разливки присутствует тонкий слой неэлектропроводного шлака.
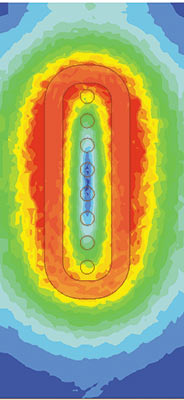
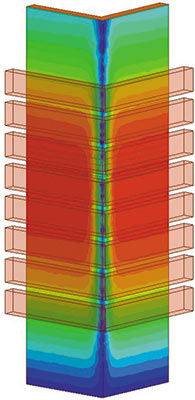
Рис. 3. Распределение вихревых токов в медной гильзе
Измерять уровень приходится по тепловому распределению в стенке кристаллизатора. При изменении уровня температурное распределение перемещается с запаздыванием.
Для оценки этого запаздывания и разработки алгоритма обработки сигнала необходимо рассматривать тепловые процессы в динамике, поэтому для решения тепловой задачи был использован модуль Mechanical, содержащий решатель для нестационарных тепловых полей Transient Thermal. Для связи областей физики была задана зависимость электропроводности меди от температуры. Методика моделирования заключалась в решении нестационарной тепловой задачи и передаче температурных распределений в Maxwell, где производился пересчет проводимости с учетом температур и решалась квазистационарная электромагнитная задача.
Для решения тепловой задачи необходимо задать граничные условия третьего рода: температура на границе медь — вода и температура расплавленного металла. При расчетах используются коэффициенты теплоотдачи λ от стали к медной стенке, учитывающие средние свойства шлакового слоя в верхней части гильзы. В действительности коэффициент теплоотдачи убывает по высоте гильзы. В модели было принято допущение постоянства коэффициентов, их значения, полученные экспериментально.
На рис. 4 показаны распределения температуры по высоте гильзы, полученные экспериментальным путем и в результате упрощенного расчета. Упрощенная тепловая модель позволяет точно рассчитать температуру стенки в зоне мениска стали, но дает завышенные значения температуры в нижней части гильзы.
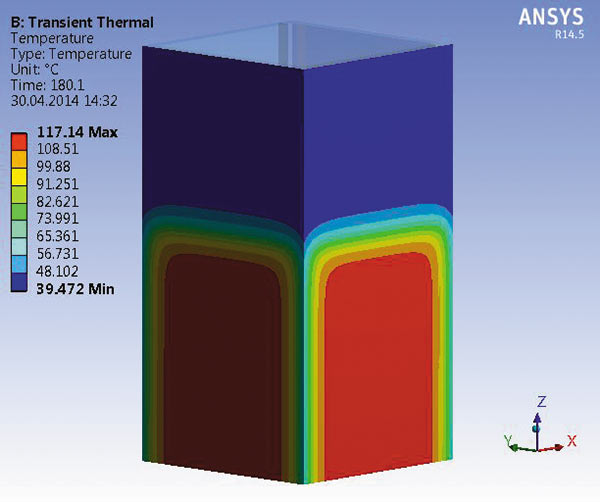
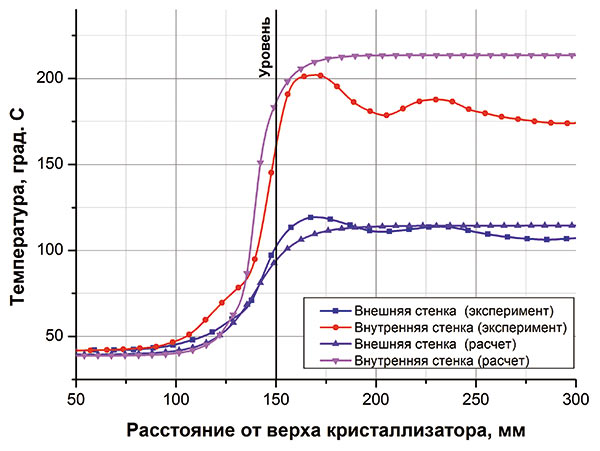
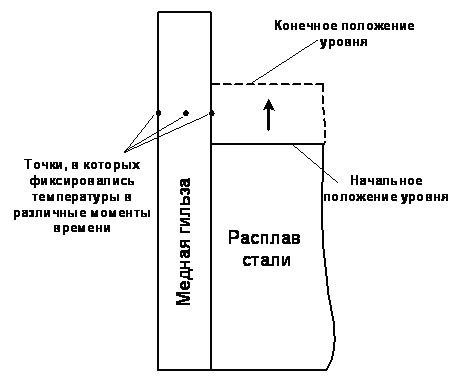
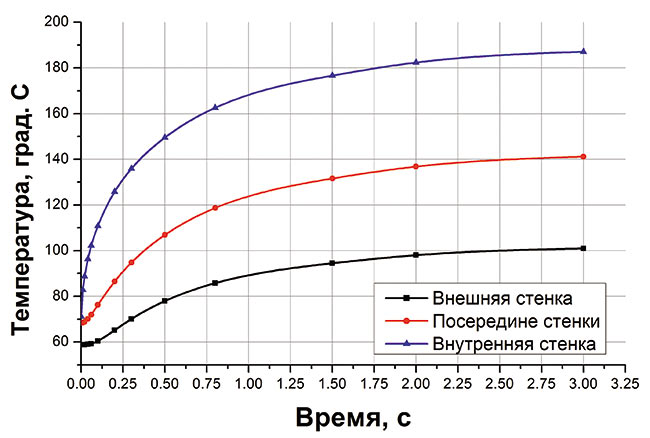
Рис. 5. Переходный тепловой процесс в гильзе кристаллизатора
при скачкообразном изменении уровня
Сложность контроля уровня по тепловому распределению состоит в том, что гильза прогревается не мгновенно, а с запаздыванием (рис. 5). Большая часть сигнала ДУМ обусловлена вихревыми токами на поверхности медной гильзы, температура которой меняется с отставанием около 23 с относительно уровня расплава. Это запаздывание необходимо сокращать до долей секунды.
В результате моделирования получены сигналы от изменения уровня с различной скоростью. На рис. 6 представлены годографы вносимого нагревом напряжения при скачкообразном изменении уровня и медленном изменении уровня. Под медленным понимается такое изменение уровня, при котором тепловое распределение соответствует уровню расплава в любой момент времени. Нелинейность годографа позволяет отслеживать быстрые изменения уровня путем проецирования сигнала на прямую, ортогональную годографу от медленного изменения.
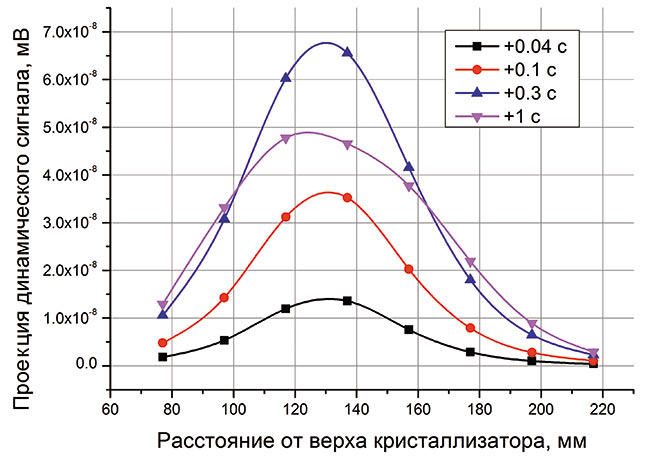
Рис. 6. Годограф вносимого сигнала от быстрого и медленного изменения уровня
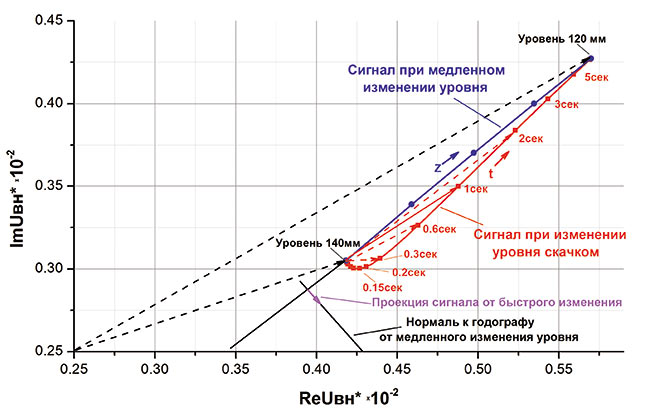
Рис. 7. Распределение проекций сигнала от быстрого изменения уровня
Для обеспечения требуемого быстродействия датчика следует умножить распределение проекций (рис. 7) на весовые коэффициенты и прибавить его к распределению вносимых от нагрева ЭДС. В результате получается скорректированное распределение, соответствующее реальному положению уровня в любой момент времени.
При таком алгоритме необходимо, чтобы угол между годографами от быстрого и медленного изменения уровня был близок к 90°. Исходя из этого была определена оптимальная частота тока возбуждения. Для медной стенки толщиной 10 мм частота равна 200 Гц, для стенки 15 мм — 80 Гц.
Расчет по совместной электромагнитнотепловой модели позволил в короткие сроки разработать алгоритм контроля уровня по тепловому распределению, в результате которого обеспечивается запаздывание менее 0,3 с. Алгоритм одинаков для обеих конструкций датчика. Сигнал проходного датчика на 15% больше, чем сигнал накладного.


