Программное обеспечение — инструмент разрешения споров

Сергей Пахомов
Начальник лаборатории, ЗАО «МНИТИ» (Московский научно-исследовательский телевизионный институт)

С помощью программы Autodesk Inventor было показано, что цилиндрические эвольвентные передачи работают несопряженными профилями. Несопряженными профилями работают и передачи с зацеплением Новикова. Были сформулированы условия для компьютерного моделирования любого цилиндрического зацепления. Показано, что зубчатые колеса можно нарезать без зуборезных станков и специализированного инструмента.

На протяжении многих лет продолжается дискуссия между сторонниками эвольвентных зубчатых передач и специалистами по зацеплению Новикова. При этом и те и другие специалисты по зубчатым передачам для своих аргументов не использовали компьютерные программы [1].

Иногда компьютерный анализ недостатков и достоинств сравниваемых зацеплений (например, с помощью компьютерной программы АРМ WinMachine) приводил к созданию новой зубчатой передачи, о которой писали как об элементе научно­технического прогресса [2].

Очевидно, что программное обеспечение является всего лишь инструментом, но только в руках специалиста оно становится мощнейшим орудием прогресса. Так, программа трехмерного моделирования Inventor способна создавать на экране монитора свои модели с точностью до восьмого знака после запятой.

Для сравнения: самые современные авиационные зубчатые колеса создаются с точностью в сто тысяч раз грубее своих компьютерных аналогов на мониторе [3]. Отсюда напрашивается идея использовать программу трехмерного моделирования не только для создания новых зацеплений, но и для проверки традиционных передач, в отношении которых ведутся многолетние споры.

С этой целью в ЗАО «МНИТИ» был предложен способ создания сопряженных профилей, который, опираясь на известные закономерности, установил определенную последовательность нарезания зубчатых колес для полуобкатной зубчатой передачи. Затем эта последовательность была воспроизведена с большой точностью на экране монитора с помощью программы трехмерного моделирования Inventor.

Из теории зацеплений известно, что делительные окружности, совпадающие с начальными окружностями, по своим свойствам качения без скольжения соответствуют центроидам.

Когда контактирующие поверхности начальных окружностей заменяются зубьями, то эти зубья должны располагаться так, чтобы независимо от того, входят зубья в зацепление или выходят из него, сохранялись постоянные угловые скорости, а следовательно, и передаточное отношение пары. Профили зубьев зубчатой передачи, которые отвечают этим требованиям, сопряжены друг с другом [4].

 Именно постоянство передаточного отношения является первым и основным критерием, по которому создаются и сравниваются цилиндрические зубчатые передачи.

Теоретически это требование прописано в теореме Виллиса, а на практике оно реализуется при нарезании зубчатых колес методом деления или методом обкатки.

Оба метода нарезания зубчатых колес имеют производственные недостатки, а именно: сложная конструкция зуборезного инструмента и недостаточная точность делительных устройств. Кроме того, результат профилирования становится известен только после нарезания зубчатых колес.

Другое дело — компьютерное моделирование. Обеспечивая создание виртуальных образов нарезаемых профилей с большой точностью, оно позволят анализировать геометрию сопряженных профилей до изготовления их в материале.

Известно, что теоретически построить зубчатый механизм можно с самыми различными профилями зубьев [5]; важно лишь, чтобы обкатывание инструмента производилось по тем же центроидам нарезаемых колес, которые будут у колес при сцеплении друг с другом [6].

Например, в отношении эвольвентного зацепления существует устойчивое мнение, что с помощью эвольвентного долбяка нарезаются эвольвентные колеса [7].

Проверим это утверждение с помощью компьютерного моделирования в среде Inventor.

Оставим на эвольвентном долбяке только один зуб (рис. 1).

Рис. 1. Долбяк с одним эвольвентным зубом

Заставим долбяк с одним зубом одновременно вращаться вокруг своей оси и вокруг оси неподвижной заготовки. При этом подвижную центроиду долбяка обкатываем без скольжения по неподвижной центроиде заготовки колеса. Тогда эвольвентные кромки зуба долбяка будут занимать последовательные положения, огибающая к которым, как известно, и будет формировать геометрию сопряженного профиля нарезаемого зуба. В дифференциальной геометрии эту огибающую, которая имеет петли и точки возврата, относят к удлиненной эпициклоиде, но не к эвольвенте.

В результате вместо ожидаемой эвольвенты зуб будет создавать профиль, характерный для циклоидального зацепления.

Таким образом, последовательность нарезания эвольвентным зубом долбяка сопряженного профиля, реализованная в программе Inventor, и ее компьютерный рисунок (рис. 2) показывают, что традиционный способ нарезания цилиндрических зубчатых колес методом обкатки не обеспечивает возможности получения эвольвентных колес.

Рис. 2. Компьютерный рисунок создания эпициклоиды

Описанный порядок действий с зубом эвольвентного долбяка, в результате которого получено циклоидальное зацепление, позволяет сформулировать общее правило для создания любой другой передачи, отличающейся от эвольвентной.

Необходимой и достаточной информацией для компьютерного моделирования любого цилиндрического зацепления является точная геометрия зуба первого колеса и передаточное число, которое требуется реализовать в проектируемой передаче из двух колес.

 Этому правилу не соответствуют зубчатые передачи ни с зацеплением Новикова, ни с зацеплением Гребенюка. В лучшем случае, для них можно определить отклонения геометрии примененных у них режущих инструментов от их идеальных компьютерных аналогов.

 Если контур зубчатого венца колеса представить как траекторию перемещения режущих кромок инструмента, например концевой фрезы (рис. 3), то он может служить исходной информацией для станка с ЧПУ.

Современные станки с ЧПУ способны реализовать любые профили зубчатых колес (рис. 4) [8].­ В ЗАО «МНИТИ» для нарезания полуобкатных циклоидальных зубчатых колес был использован вертикально­фрезерный станок под управлением системы FANUC.

Технология нарезания полуобкатного циклоидального зацепления с помощью станков с ЧПУ была опробована при изготовлении приводов нестандартного оборудования и показала возможность создания зубчатых передач без специализированных зуборезных станков и специального для них инструмента (рис. 5).

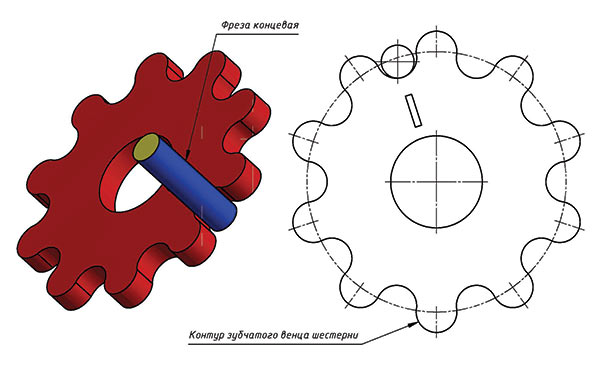
Рис. 3. Схема нарезания зубчатого колеса концевой фрезой

Рис. 4. Технология нарезания зубчатого колеса на станке ЧПУ

Рис. 5. Фрагменты циклоидальных передач наружного и внутреннего зацеплений

Выводы:

1. Компьютерное моделирование на экране монитора может создать сопряженные профили зубьев колес зацепления, имеющие большую точность, если известен профиль одного из колес и передаточное число передачи.
2. Порядок компьютерного моделирования сопряженных колес может служить проверкой реализации передаточного отношения.
3. Эвольвентные передачи, зубчатые передачи с зацеплением Новикова и Гребенюка передают крутящие моменты несопряженными поверхностями своих зубьев.
4. Современные станки с ЧПУ могут по созданным объемным компьютерным моделям нарезать любые цилиндрические зубчатые колеса без использования специализированных зуборезных станков и зуборезного инструмента, предназначенного для них. 

Литература:

1. Лопатин Б.А., Хаустов С.А. Автоматизированная система моделирования и анализа способов формирования зубьев зубчатых колес // Челябинск: Вестник ЮУрГУ. 2008. № 10.
2. Андросов А., Гребенюк Г.П. Зубчатые передачи с эллиптическим профилем зуба как элемент научно­технического прогресса в машиностроении // САПР и графика. 2005. № 8.
3. Производство зубчатых
   колес газотурбинных двигателей /[Елисеев Ю.С., Кры­мов В.В., Нежурин И.П., Новиков В.С., Рыжов Н.М.]. М.: Высшая школа, 2001. 495 с.
4. Калашников С.Н., Калашников А.С. Зубчатые колеса и их изготовление. М.: Машиностроение, 1983. 263 с.
5. Артоболевский И.И. Теория механизмов. М.: Наука, 1967. 719 с.
6. Литвин Ф.Л. Теория зубчатых зацеплений. М.: Наука, 1968. 584 с.
7. Металлорежущие инструменты /[Сахаров Г.Н., Арбузов О.Б., Боровой Ю.Л., Гречишников В.А., Киселев А.С.]. М.: Машиностроение, 1989. 328 с.
8. Пахомов С.Н. Технология полуобкатного зацепления // Техника средств связи. Серия техника телевидения. М.: ЗАО «МНИТИ». 2013.
   С. 67­73.

САПР и графика 8`2014