Применение оптимизационных методов и интерактивного блокирующего контура при выборе коэффициентов смещения (корригировании) цилиндрических эвольвентных зубчатых передач внешнего зацепления

Валерий Голованёв,
инженер-аналитик, программист

Введение

Требования к повышенной прочности, долговечности, износостойкости и плавности работы зубчатых передач были, есть и будут приоритетными при проектировании зубчатых передач. Широкие возможности для удовлетворения этих требований предоставляет так называемое корригирование эвольвентных зубчатых колес. Сущность корригирования сводится к использованию различных участков одной и той же эвольвенты. Корригирование производится путем изменения положения (смещения) инструмента относительно заготовки в станочном зацеплении. Именно корригирование позволяет без материальных затрат с помощью стандартного инструмента изменять форму и размеры зубьев, варьировать качественные показатели и нагрузочную способность передачи, вписывать передачу в требуемое межосевое расстояние, а также проектировать работоспособные передачи, функционирование которых при нулевых смещениях просто невозможно (например, с пятью­шестью зубьями на малой шестерне).

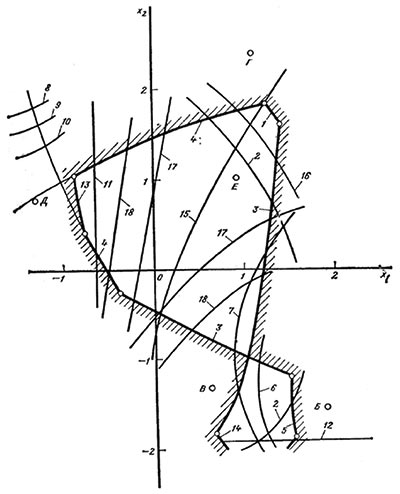
Рис. 1. Блокирующий контур передачи внешнего зацепления, составленной из колес, нарезанных реечным инструментом

Показателями, отражающими корригирование зубчатой пары, являются коэффициенты смещения исходного контура — x1 и x2.

Наглядным способом отображения зависимости геометрических параметров и качественных показателей передачи от коэффициентов смещения являются кривые, построенные для каждого сочетания чисел зубьев передачи z1 и z2 в плоской системе координат x1 и x2. Эта система координат была предложена М.Б. Громаном [1], а в дальнейшем получила развитие в работах В.А Гавриленко [13] и коллектива, возглавляемого И.А. Болотовским. Именно В.А. Гавриленко предложил термин «блокирующий контур зубчатой передачи».

Суть блокирующего контура (БК) — рис. 1 [2] состоит в том, чтобы на плоскости координат x1, x2 в виде набора линий показать основные ограничения, в пределах которых будет обеспечена кинематически правильная работа зубчатой передачи.

Таковыми ограничениями (изо­линиями) являются:

• предельно допустимое минимальное значение коэффициента торцового перекрытия εα = 1 (при εα < 1 будет нарушена непрерывность зацепления зубьев в передаче);
• интерференция в рабочем зацеплении;
• границы допустимого подрезания;
• предельно допустимое минимальное значение нормальной толщины зуба на поверхности вершин зубьев sna = 0;
• срезание зуба зубчатого колеса зуборезным долбяком при обработке колеса инструментом.

Внутри блокирующего контура могут быть проведены линии условных границ, за которые переходить не рекомендуется: εα = 1,2, sna = 0,4mn, линии x1 = xmin1 и x2 = xmin2, ограничивающие начало подрезания, а также линия x1 + x2 = 0 (при расчете передачи по коэффициентам смещения) или линия x1 + x2= xΣ (при расчете передачи с фиксированным межосевым расстоянием).

Кроме того, представляет интерес линия выравнивания удельных скольжений (ЛВУС) в нижних точках активных профилей зубьев θp1= θp2. По сути, эта линия является критерием износостойкости передачи. Выделение этой линии на БК было сделано И.А. Болотовским [3] на основании работ Я.И. Дикера [4].

Многие ученые задавались вопросом о принципах рационального выбора коэффициентов смещения. Не вызывают сомнений выводы И.А. Болотовского [3] о том, что параметры рациональной коррекции зависят от условий работы и вида наиболее вероятного разрушения зубьев, от материалов, из которых изготовлены колеса, и их термообработки, от способа изготовления зубчатых колес, от класса точности передачи и т.д.

Более подробная информация об использовании блокирующих контуров при проектировании эвольвентных цилиндрических передач дана автором в совместной статье с профессором Д.Т. Бабичевым [13].

Методы оптимизации, интерактивный блокирующий контур и расчет передачи

Создание альбомов блокирующих контуров зубчатых передач коллективом под руководством И.А. Болотовского [8, 9, 10] обеспечило конструкторов и расчетчиков мощным инструментом по подбору коэффициентов смещения, однако не решило задачу оптимального выбора параметров корригирования. Подбор коэффициентов требовал от конструктора определенных профессиональных навыков и неоднократного выполнения трудоемких расчетов передачи.

C появлением ПЭВМ задача построения интерактивного блокирующего контура уже решалась [11], однако основной целью построения было использование при интерактивном проектировании многократно строящихся БК, на которых в процессе проектирования изменялись границы полей допустимых значений и перемещались линии качественных показателей.

В настоящее время задачей оптимального выбора коэффициентов смещения зубчатой передачи должна заниматься компьютерная программа, использующая для поиска решений методы оптимизации. В данном случае проектируемая зубчатая передача представляется в виде математической модели с заданной совокупностью критериев и системой геометрических ограничений по параметрам зацепления. А интерактивный БК должен служить удобным средством визуализации системы ограничений и линий качественных показателей зацепления.

Что же представляет собой математическая модель зубчатой передачи? По сути, это геометрический расчет, выполняемый по ГОСТ 16532­70 [6], и расчет на прочность, выполняемый по ГОСТ 21354­87 [7], с целевой функцией, выстраиваемой по одному или по совокупности критериев.

Для построения линий БК, помимо математической модели зубчатой передачи, необходимы методы поиска линий экстремумов для тех или иных показателей (геометрических и прочностных) в двумерном поле значений коэффициентов смещения.

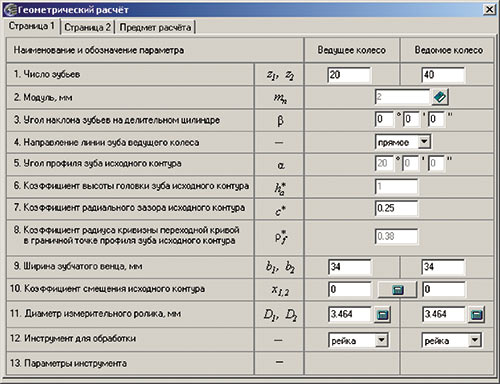
Рис. 2. Диалоговое окно «Геометрический расчет»

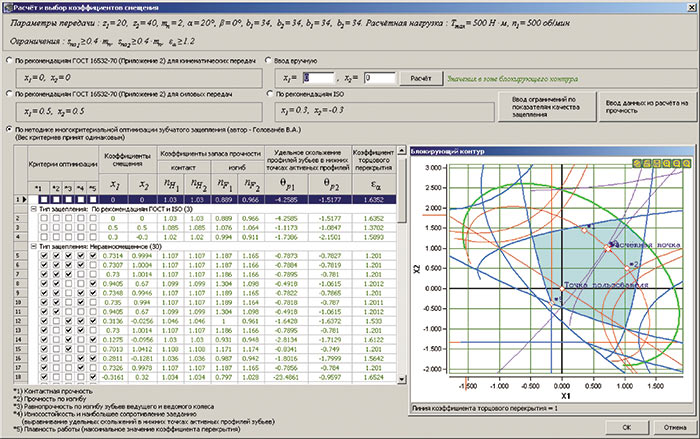
Рис. 3. Диалоговое окно «Расчет и выбор коэффициентов смещения»

Эти аспекты были использованы при разработке подсистемы расчета и выбора коэффициентов смещения для модуля расчетов цилиндрической зубчатой передачи внешнего зацепления (рис. 2 и 3), входящего в комплекс программ КОМПАС­GEARS, который, в свою очередь, является частью разработанного автором статьи приложения «Валы и механические передачи 3D» для системы трехмерного моделирования КОМПАС­3D российской компании АСКОН.

В качестве метода оптимизации для решения поставленной задачи была выбрана программная реализация метода SUMT Фиакко и Маккормика [5].

После визуализации основного диалогового окна подсистемы (рис. 3) автоматически строится ИБК. Далее пользователь может вручную выбрать точку с коэффициентами смещения x1 и x2 непосредственно на поле или запустить оптимизационный расчет для нахождения коэффициентов x1 и x2.

В результате выполнения оптимизационного расчета будут найдены решения, отражающие все возможные сочетания пяти критериев:

• контактной прочности (запас прочности по контактным напряжениям);
• прочности по изгибу (запас прочности по изгибным напряжениям);
• равнопрочности по изгибу зубьев ведомого и ведущего колеса;
• износостойкости и наибольшего сопротивления заеданию;
• плавности работы передачи.

Новые линии в блокирующем контуре зубчатой передачи

После выполнения расчета в ИБК дополнительно строятся:

• линия равнопрочности по изгибу зубьев ведущего и ведомого колеса (ЛРПИ);
• линия минимальных контактных напряжений (ЛМКН) (линия значений x2, при которых при заданном x1 значение контактных напряжений будет минимально).

Эти линии строятся с учетом:

• реально заданной нагрузки из расчета на прочность при максимальной нагрузке (ГОСТ 21354­87 [7]);
• механических свойств материалов ведущего и ведомого колеса;
• схемы работы передачи.

Для удобства восприятия линия выравнивания удельных скольжений, линия равнопрочности по изгибу и линия минимальных контактных напряжений выделены в отдельную цветовую группу, которую назовем Группой линий механических показателей зацепления.

При этом установлено следующее:

• линия равнопрочности по изгибу (ЛРПИ) проходит, как правило, рядом с линией выравнивания удельных скольжений;
• линия минимальных контактных напряжений (ЛМКН) пересекает линию равнопрочности по изгибу и линию выравнивания удельных скольжений (ЛВУС). При этом чаще всего для прямозубых передач ЛМКН расположена выше зоны блокирующего контура, а для косозубых передач ЛМКН проходит через зону блокирующего контура (рис. 4).

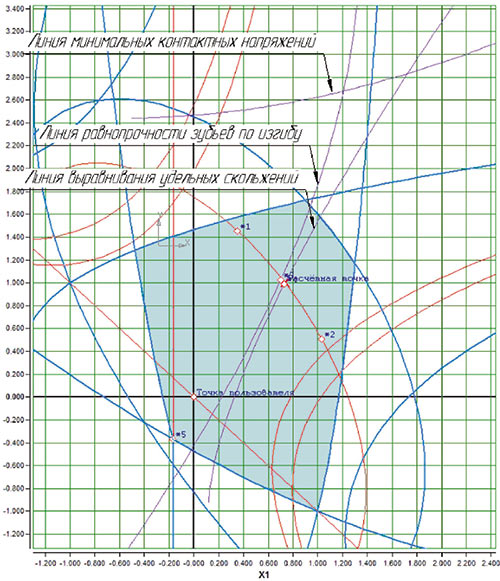
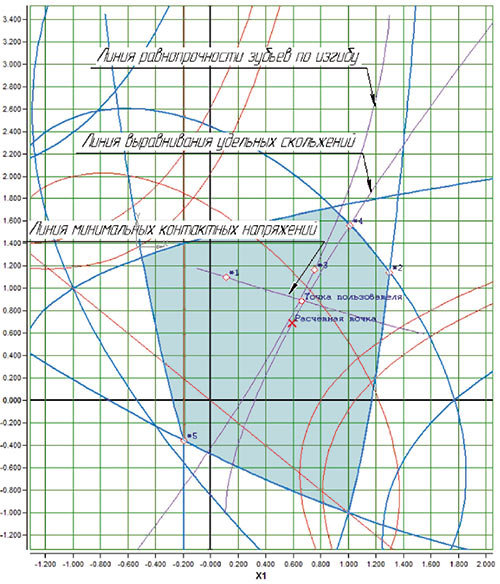
Рис. 4. Линии механических показателей зацепления: a — для прямозубой передачи, б — для косозубой передачи (точка *1 — оптимальная точка по критерию контактной прочности, *2 — по изгибной прочности, *3 — по равнопрочности на изгиб, *4 — по износостойкости и заеданию, *5 — по плавности работы)

Можно было бы предположить, что для косозубых передач вопрос визуальной локализации передач с оптимальными характеристиками прочности и износостойкости следует считать решенным — оптимальной считалась бы точка, находящаяся на ЛМКН между точкой ее пересечения с ЛВУС и точкой пересечения с ЛРПИ. Эта точка (точка пользователя на рис. 4б), безусловно, будет очень близка к оптимальности, но положение реальной точки экстремума, определенного по совокупности трех критериев, соответствующих этим линиям, может быть несколько иным.

Изополя коэффициентов запаса контактных и изгибных напряжений в блокирующем контуре

Продолжением работ по построению линии минимальных контактных напряжений стали работы по построению совокупности изолиний (изополей) коэффицентов запаса прочности. Так, для прямозубой передачи форма изополей будет такой, как показано на рис. 5 и 6.

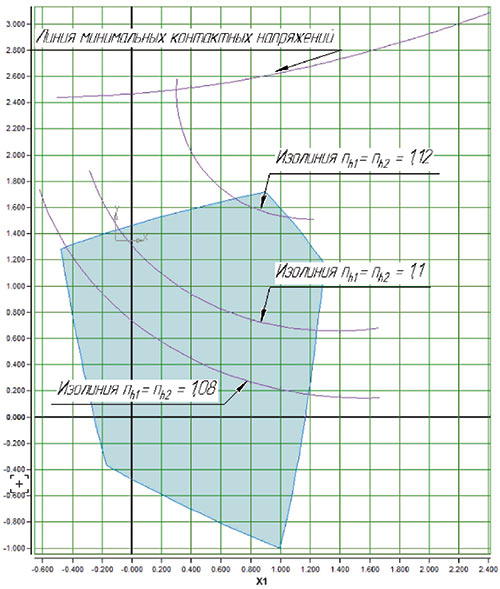
Рис. 5. Изополя коэффициентов запаса контактных напряжений для прямозубых передач

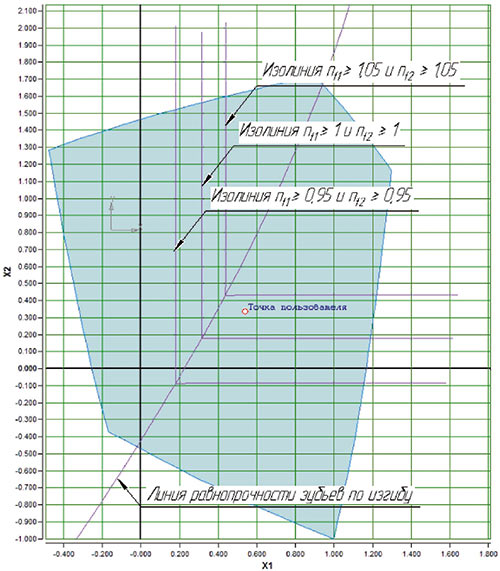
Рис. 6. Изополя коэффициентов запаса изгибных напряжений для прямозубых и косозубых (β < 10º) передач

При этом «прямоугольная» форма изополей коэффициентов запаса изгибных напряжений сохраняется для прямозубых передач и передач с малыми углами наклона β (до 10º). Для косозубой передачи с углом наклона β = 15º форма изополей коэффициентов запаса изгибных напряжений существенно меняется.

Линии изополей коэффициентов запаса контактных напряжений четко группируются вокруг рассмотренной выше линии минимальных контактных напряжений (рис. 7 и 8).

Дальнейшее использование изополей просто и понятно. Передача с искомыми значениями коэффициентов запаса будет находиться в зонах, расположенных между линиями изополей.

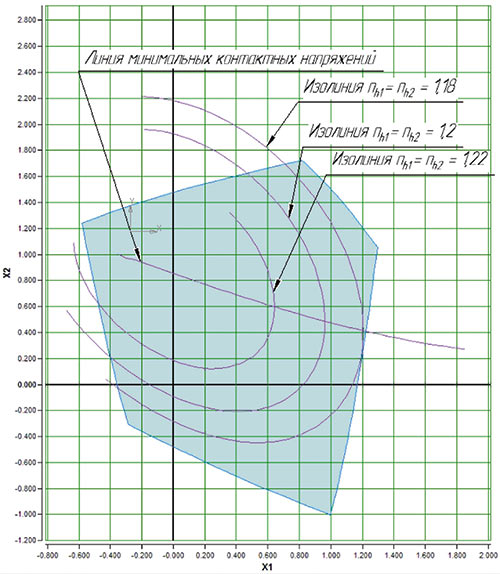
Рис. 7. Изополя коэффициентов запаса контактных напряжений для косозубых передач (β > 0º)

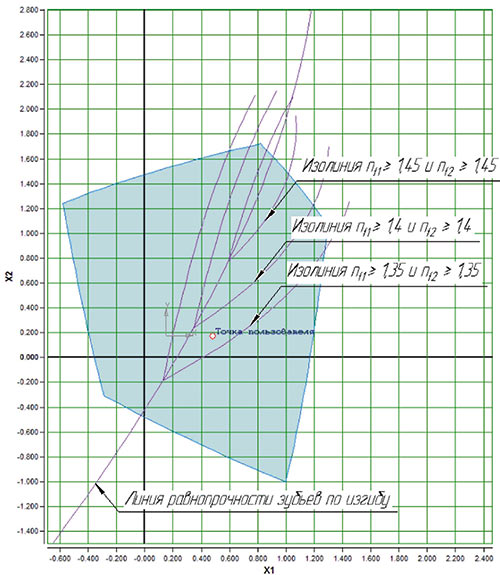
Рис. 8. Изополя коэффициентов запаса изгибных напряжений для косозубых передач (β > 10º)

Работа с интерактивным блокирующим контуром

Интерактивный блокирующий контур представлен в отдельном окне.

После выполнения оптимизационного расчета в поле ИБК будут поставлены пять точек, соответствующих выполненным расчетам индивидуально по каждому из критериев, а также шестая точка, являющаяся результирующей по совокупности всех пяти критериев (рис. 9).

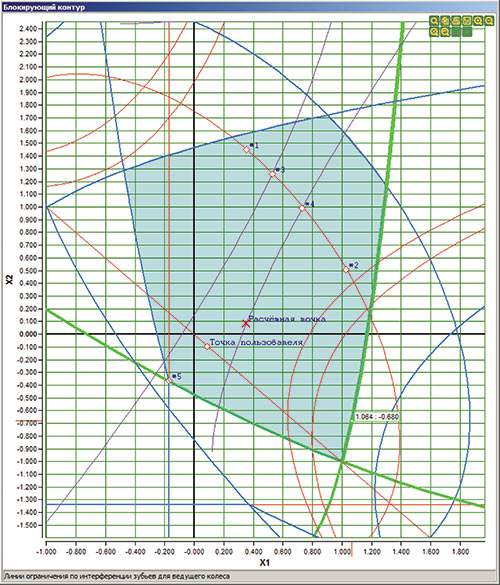
Рис. 9. Увеличенное окно с интерактивным блокирующим контуром

В дальнейшем пользователь сможет отобразить в поле ИБК расчетную точку, найденную по любому из вариантов расчета, либо выбрать в поле ИБК любую точку (в том числе и находящуюся за пределами ограничительных линий) для выполнения ручного расчета.

По любому из вариантов расчета могут быть просмотрены результаты геометрического расчета и расчета на прочность (рис. 10 и 11).

Выполнена визуализация зацепления (рис. 12).

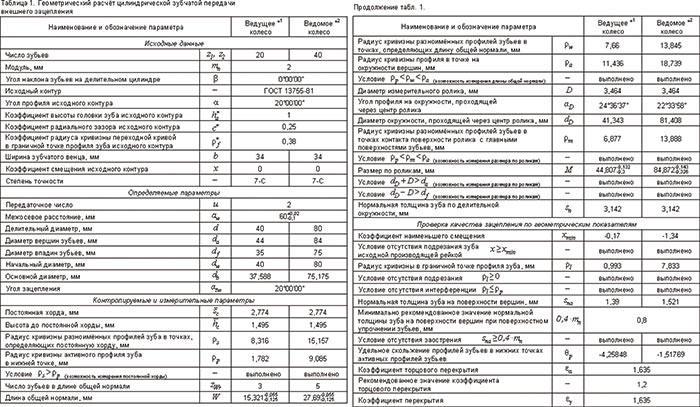
Рис. 10. Результаты геометрического расчета

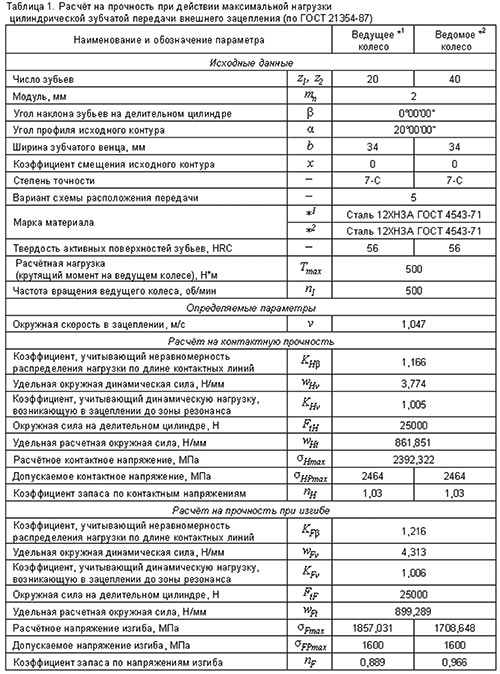
Рис. 11. Результаты расчета на прочность при действии максимальной нагрузки

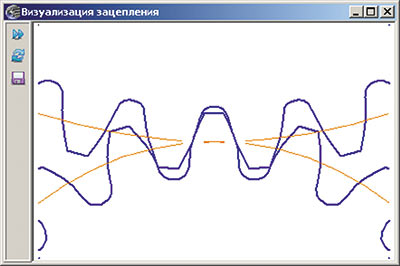
Рис. 12. Визуализация зацепления

Дополнения

1. Помимо режима работы основного диалогового окна «Расчет и выбор коэффициентов смещения» со встроенным окном ИБК возможен режим работы, когда окно ИБК вынесено за пределы основного окна. В этом случае в таблице результатов отображаются дополнительные колонки с параметрами (рис. 13).
2. Форма отображаемого ИБК меняется в случае использования в качестве зуборезного инструмента долбяка. При этом учитывается степень его износа. Соответственно будут меняться и результаты многокритериального оптимизационного расчета (рис. 14a,б).
3. При необходимости принятые ограничения по показателям качества зацепления могут быть изменены (рис. 15). Например, установлен нижний предел коэффициента минимально допустимого значения нормальной толщины зуба, равный «0.25» или другому значению не меньше «0»; установлено минимально допустимое значение коэффициента торцового перекрытия, равное «1» или другому значению.

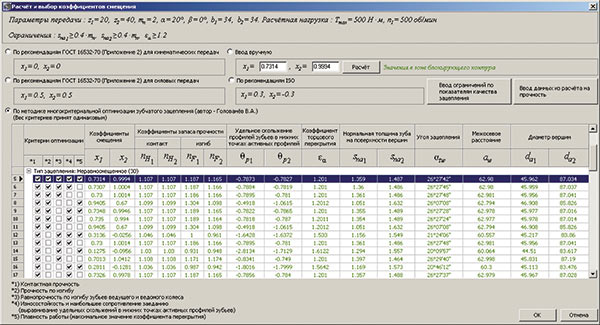
Рис. 13. Расширенный режим работы основного диалогового окна «Расчет и выбор коэффициентов смещения»

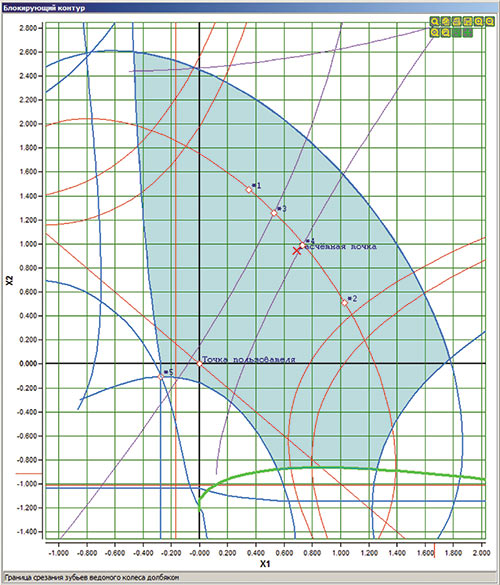
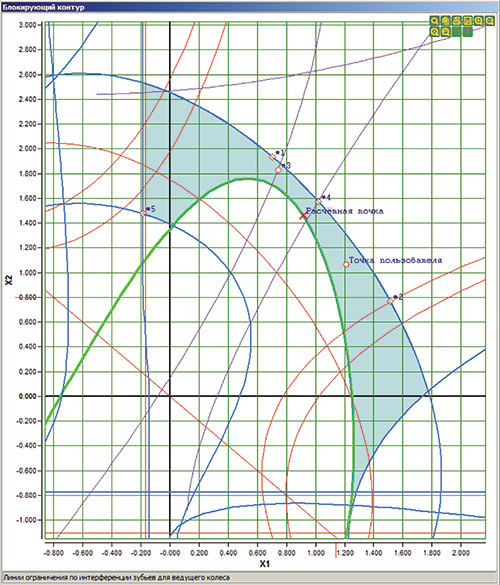
Рис. 14. Форма ИБК при обработке зуборезным долбяком (новый (а) и изношенный (б) долбяк)

Рис. 15. Ввод ограничений по показателям качества зацепления

Основные результаты работы

1. Построена математическая модель зубчатой передачи с системой ограничений, пригодная для использования в методах оптимизации.
2. Выполнена программная реализация построения интерактивного блокирующего контура.
3. Реализована методика многокритериальной оптимизации зубчатого зацепления, позволяющая конструктору с любой квалификацией быстро решить задачу подбора оптимальных значений коэффициентов смещения, исходя из критериев функционирования проектируемой передачи, при этом одновременно решая задачи повышения прочности и долговечности зубчатых передач без изменения технологии производства.
4. Введены новые линии блокирующего контура — линия равнопрочности по изгибу зубьев ведущего и ведомого колеса и линия минимальных контактных напряжений.
5. Введено понятие изополей коэффициентов запаса контактных и изгибных напряжений в блокирующем контуре, рассмотрена их форма для прямозубых и косозубых передач.
6. Принимая во внимание широкое распространение системы КОМПАС­3D, а также популярность модуля «Валы и механические передачи 3D», можно предположить, что предложенная методика расчета коэффициентов смещения зубчатых передач с использованием блокирующего контура будет востребована и специалистами предприятий, и преподавателями в учебном процессе, и студентами.

Список литературы:

1. Громан М.Б. Подбор коррекции зубчатых передач // Вестник машиностроения. 1955. № 2.
2. Болотовский И.А., Безруков В.И., Васильева О.Ф. и др. Справочник по геометрическому расчету эвольвентных зубчатых и червячных передач / Под ред. И.А. Болотовского. — 2­е изд. — Машиностроение, 1986. 448 с.
3. Болотовский И.А. К вопросу о рациональном выборе коэффициентов смещения зубчатых передач // Тр. Уфимского авиационного института. Уфа. 1957. Вып. 3. С. 75­102.
4. Дикер Я.И. Таблица расчета зацеплений зубчатых передач. Оргаметалл, 1937.
5. Банди Б. Методы оптимизации. Вводный курс: Пер. с англ. — М.: Радио и связь, 1988. 128 с: ил.
6. ГОСТ 16532­70. Передачи зубчатые цилиндрические эвольвентные внешнего зацепления. Расчет геометрии. М.: Изд­во стандартов, 1983. 41 с.
7. ГОСТ 21354­87. Передачи зубчатые цилиндрические эвольвентные внешнего зацепления. Расчет на прочность. М.: Изд­во стандартов, 1988. 127 с.
8. Болотовская Т.П., Болотовский И.А., Смирнов В.Э. Альбом блокирующих контуров. Расчет коррекции зубчатых колес с помощью блокирующих контуров. Справочное руководство для конструкторов машиностроительных предприятий. Уфа, 1958. 189 с.
9. Болотовская Т.П., Болотовский И.А., Бочаров Г.С. и др. Справочник по корригированию зубчатых колес. М.: Свердловск: Машгиз, 1962. 215 с.
10. Болотовская Т.П., Болотовский И.А., Бочаров Г.С. и др. Справочник по корригированию зубчатых колес / Под ред. И.А. Болотовского. Ч.2: Зубчатые передачи внешнего и внутреннего зацепления, составленные из колес, нарезанных долбяками. М.: Машиностроение, 1967. 576 с.
11. Гольдфарб В.И., Ткачев А.А. Проектирование эвольвентных цилиндрических передач. Новый подход. Ижевск: Изд­во ИжГТУ, 2004. 94 с.
12. Голованёв В.А., Бабичев Д.Т. Использование блокирующих контуров при проектировании эвольвентных цилиндрических передач: состояние, проблемы, перспективы. http://machinery.ascon.ru/source/info_materials/2014/V.%20Golovanev_and_D.Babichev.pdf — 2014. 31 с.
13. Гавриленко В.А. Основы теории эвольвентной зубчатой передачи. М.: Машиностроение, 1969. 431 с. 

САПР и графика 11`2014