Циклоидальный и псевдоциклоидальные овалы

Виктор Чебыкин

Введение

Изучая литературу по овальным кривым, автор нигде не встретил упоминания о циклоидальном овале. А вот циклоиде, напротив, повезло — ей посвящали чуть ли не оды. Эту «замечательную» и «загадочную» кривую изучали и описывали десятки известных математиков начиная с XVI века. В статье «Классификация и идентификация эллипсовидных овальных кривых» (см. «САПР и графика». 2014. № 3. С. 92­94) автор попытался доказать, что циклоидальный овал, так же как и «прародительница», не только имеет право на существование, но и по своим свойствам и геометрии является уникальной кривой. Чего только стоят четырнадцать констант этого овала. Найдется ли еще кривая с таким обилием констант? Кстати, циклоидальный овал является также «родоначальником» бесконечного ряда овальных кривых, которые, предположительно, пока никем не описаны. Присвоим им имя — «псевдоциклоидальные овалы» (P.C.O. — аббревиатура от pseudo­cycloidal oval) и рассмотрим их чуть ниже, в одноименном разделе.

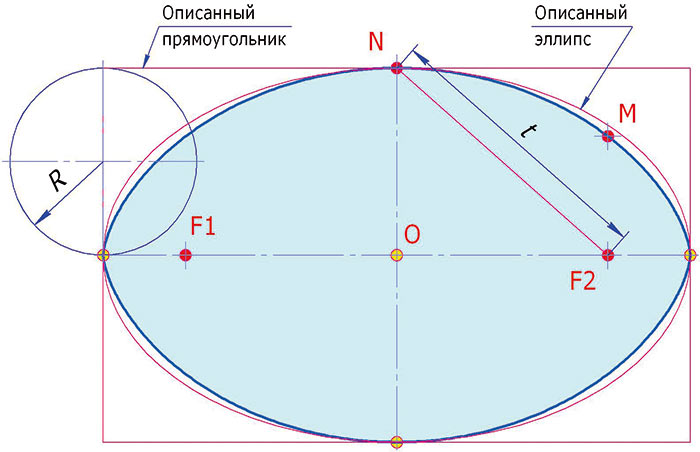
Рис. 1

Константы циклоидального овала

В упомянутой выше статье приведено только семь констант. Теперь назовем семь остальных (рис. 1), которые также определены автором:

1. Константа среднего фокального луча MLco1 = t/R ≈ 3,017 401 301 20…
2. Периметральная контрэллипсная константа Pcoe = P/Pe ≈ 0,978 444 573 32…
3. Площадная контрэллипсная константа Scoe = S/Se ≈ 0,954 929 658 55…
4. Периметральная контрпрямоугольная константа Pco□ = P/P□ ≈
   0,777 969 059 29…
5. Площадная контрпрямоугольная константа Sco□ = S/S□ = 0,75
6. Площадная константа овалоида вращения вокруг большой оси

Soxco = Sox /S ≈ 3,555 555 555 55…

7. Площадная константа овалоида вращения вокруг малой оси,

Soyco = Soy /S ≈ 4,822 026 8…

где: t — средний фокальный луч;

 R — радиус производящей окружности циклоиды;

 P — периметр овала;

 S — площадь овала;

 Pe — периметр описанного эллипса;

 Se — площадь описанного эллипса;

 P□ — периметр описанного прямоугольника;

S□ — площадь описанного прямоугольника;

Sox — площадь поверхности овалоида вращения вокруг большой оси;

Soy — площадь поверхности овалоида вращения вокруг малой оси.

Приведем формулы расчета некоторых параметров циклоидального овала и циклоидальных овалоидов:

P = 16R (вытекает из свойства — длина арки циклоиды равна 8R; свойство открыл Кристофер Рен); (1)

S = 16pR2 (вытекает из свойства — площадь под одной аркой циклоиды втрое больше, чем площадь порождающего круга; свойство открыл Галилей, математически доказал Жиль Роберваль);     (2)

Sox = 6pSoxcoR2;   (3)

Soy = 6pSoycoR2 ;  (4)

Vox = 5p2R3;  (5)

Voy = 7,727p2R3,  (6)

где: Vox — объем циклоидального овалоида вращения вокруг большой оси;

 Vcoy — объем циклоидального овалоида вращения вокруг малой оси.

Циклоидальные овалоиды изображены на рис. 2.

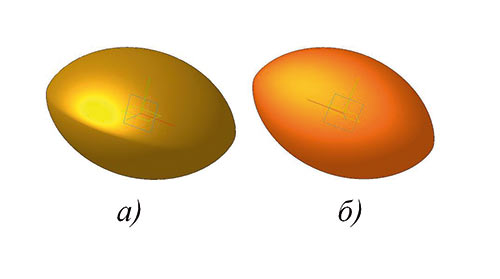
Рис. 2

Псевдоциклоидальные овалы

Псевдоциклоидальный овал — плоская гладкая замкнутая эллипсовидная овальная кривая.

Используя операцию «По сечениям» (термин КОМПАС), создадим 3D­модель наклонного циклоидального цилиндра (рис. 3). Эскизы параллельных сечений — циклоидальные овалы. При рассечении цилиндра наклонными плоскостями получаем фигуры, контуры которых внешним видом напоминают циклоидальный овал. Одни из них вытянутые по отношению к циклоидальному овалу, другие — сжатые (рис. 4). Это и есть псевдоциклоидальные овалы. Меняя угол наклона циклоидального цилиндра и угол наклона секущей плоскости, можно получить бесчисленное множество P.C.O.

Рис. 3

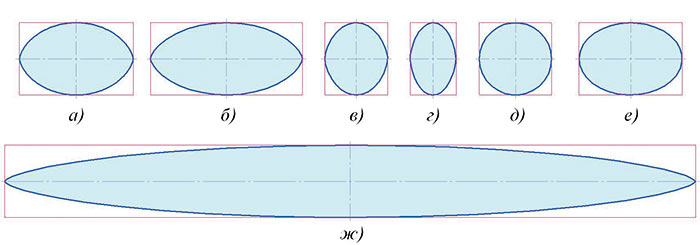
Рис. 4

Что, кроме похожей формы, унаследовали эти кривые от циклоидального овала? Имеют ли они константы? Оказывается, имеют! Это площадная контрэллипсная константа и площадная контрпрямоугольная константа, причем их численные значения совпадают с аналогичными у циклоидального овала:

• площадная контрэллипсная константа Spcoe = S/Se ≈ 0,954 929 658 55…;
• площадная контрпрямоугольная константа Spco□ = S/S□ = 0,75,

где: S — площадь овала;

Se — площадь описанного эллипса;

S□ — площадь описанного прямоугольника.

Эти константы помогут идентифицировать P.C.O. из ряда различных овальных кривых.

Псевдоциклоидальные овалы, как правило, имеют по два фокуса, но в определенных интервалах параметров могут быть бесфокусными. В сжатых псевдоциклоидальных овалах в зависимости от параметров фокусы могут располагаться как на одной, так и на другой оси.

По предложенной в упомянутой выше статье классификации все эти кривые — гипоовалы.

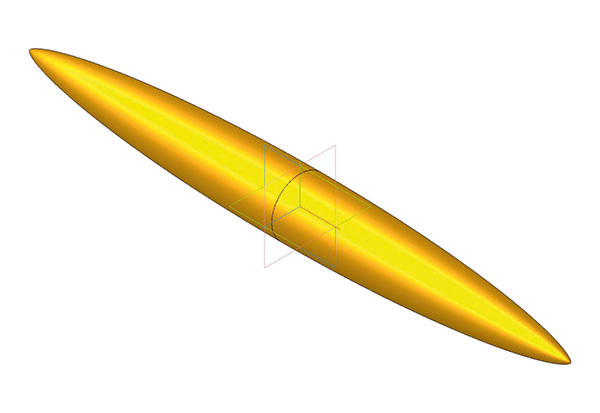
Рис. 5

Возможное применение (предположения автора): архитектура и дизайн; оптика — благодаря бесконечно большому разнообразию форм (пропорций), наличию или отсутствию фокусов и расположению фокусов; авиастроение и кораблестроение — благодаря большому диапазону аэродинамических характеристик (форма корпуса самолета, дирижабля, летающей тарелки, корабля, фрагменты крыла самолета)…

Сравним площадную контрпрямоугольную константу C.O. и P.C.O., равную 0,75, с аналогичной константой окружности и эллипса, у которых она составляет: p/4 ≈ 0,785 398 163 39….

По этой константе циклоидальный и псевдоциклоидальные овалы можно назвать эталонными овальными кривыми.

На рис. 5 показана модель одного из множества псевдоциклоидальных овалоидов. Не правда ли, она напоминает Yellow Submarine?  

САПР и графика 11`2014