Три измерения САПР — один инструмент разработчика! Моделирование, параметризация и конвертация данных в новом геометрическом ядре C3D V16

Аркадий Камнев
Менеджер по продукту C3D, компания C3D Labs

Традиционно в начале декабря дизайнеры, проектировщики и конструкторы по всему миру отмечают профессиональную дату — День компьютерной графики, или День 3D­шника. C3D Labs поздравляет своих коллег с этим замечательным праздником и объявляет, что именно 3 декаб­ря увидела свет новая версия геометрического ядра C3D V16! Коллектив разработчиков, на протяжении всего года трудившийся над новой версией, представляет пользователям обновленный набор профессиональных инструментов для разработки инженерного программного обеспечения.

Три базовые составляющие современной САПР образуют C3D:

• геометрический моделировщик C3D Modeler;
• решатель параметрических ограничений C3D Solver;
• конвертор данных C3D Converter.

От версии к версии они совершенствуются в тесном контакте друг с другом, обеспечивая целостное развитие геометрического ядра и отличную взаимосвязь его отдельных компонентов. C3D остается единственным на рынке программным компонентом, предоставляющим разработчикам все три модуля в одном продукте.

Строим модели

Команда разработки C3D Labs — это профессиональный коллектив, увлеченный одной общей идеей создания максимально удобного инструмента для разработки инженерного программного обеспечения. В работе над проектами нам часто приходится принимать нестандартные решения, выходящие за рамки привычного понимания вещей, и мы стремимся к тому, чтобы разработчики 3D­систем на базе геометрического ядра C3D тоже могли творить без границ! С этой целью мы расширили функционал для создания геометрических форм различной сложности и усовершенствовали методы построения 2D/3D­геометрии в C3D V16.

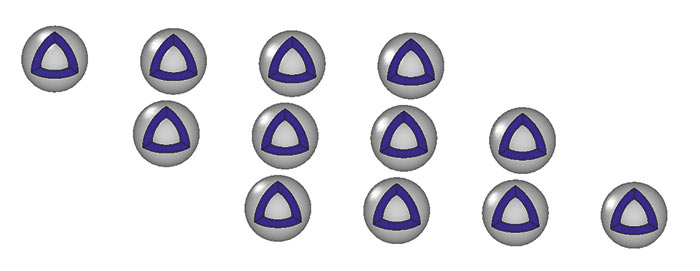
Рис. 1. Размножение тел по сетке

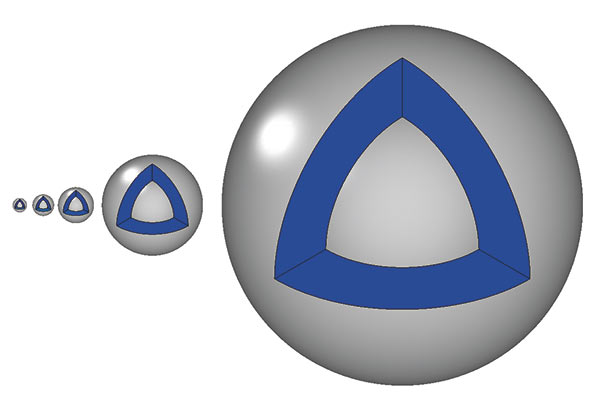
Рис. 2. Размножение тел по набору матриц трансформаций

В новой версии ядра можно размножать тела по заданной сетке (рис. 1) и по набору матриц трансформаций: поворота (изменяющих ориентацию тел в трехмерном пространстве), перемещения (изменяющих положение тел в пространстве) и масштабирования (увеличивающих размер тел) — рис. 2. В кинематической операции образующая тела размножается для разных положений относительно направляющей. Это позволяет усечь начало направляющей кривой, перенести образующую в начало усеченной направляющей и построить тело заметания, совпадающее с исходным телом на оставшемся конечном участке (рис. 3). Подверглась изменению также операция построения резьбы, которая теперь может быть адаптирована по начальному положению и длине отверстия, по которому она нарезается (рис. 4).

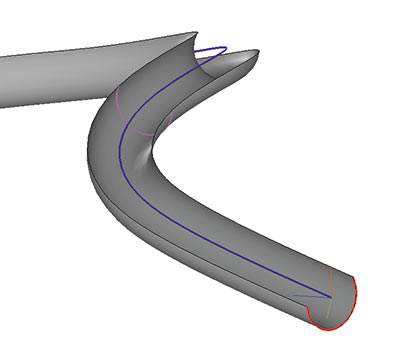
Рис. 3. Размножение образующей в кинематической операции

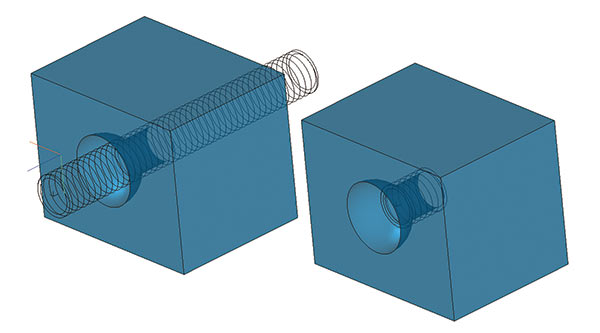
Рис. 4. Адаптация резьбы по положению и длине отверстия

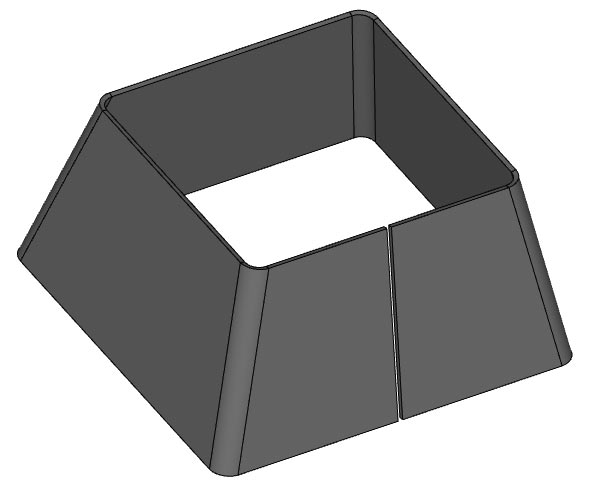
Рис. 5. Постоянный радиус сгиба при построении обечайки с уклоном граней

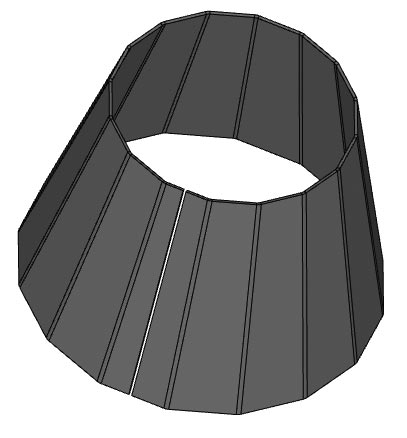
Рис. 6. Сегментация дуг отрезками для построения конусных многогранников

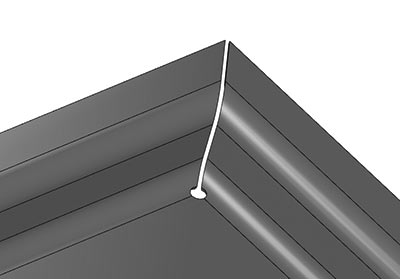
Рис. 7. Круговая обработка замыкания угла при построении листового тела

Не прекращаются работы C3D Labs по реализации новых возможностей, связанных с гибкой листового тела. В этом году раздел также был подвергнут серьезным доработкам. В частности, операция построения обечайки по одному эскизу с уклоном граней теперь выполняется с постоянным радиусом сгиба (рис. 5), а построение конусных многогранников методом гибки листового металла достигается за счет сегментации опорных дуг отрезками (рис. 6). Решена задача замыкания угла в операции построения тела из листового металла благодаря заданию круговой обработки проблемного участка (рис. 7). Кроме того, стало доступным задание разных длин слева и справа у продления сгиба, что позволяет проектировать листовые тела еще более нестандартных форм (рис. 8).

Рис. 8. Задание разных длин слева и справа у продления сгиба

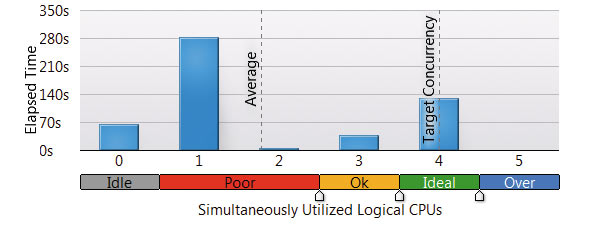
Рис. 9. Среднее время выполнения операции в C3D для разного количества одновременно используемых ядер CPU (график выполнен в среде Intel VTune Performance Analyzer)

Рис. 10. Скругление ребер в C3D V16

Рис. 11. Придание толщины поверхностям с полюсными точками

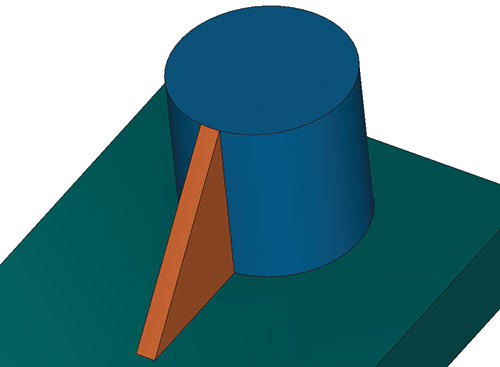
Рис. 12. Построение ребра жесткости c использованием поверхности вращения

Благодаря комплексной оптимизации построений в C3D V16 значительно ускорилось выполнение сечений и разрезов в проекционных видах, а распараллеливание расчетов при выполнении данных операций вывело геометрическое ядро на качественно новый уровень работы с 2D­геометрией. Примечательно, что для разного аппаратного обеспечения рабочих станций эти результаты изменяются в зависимости от количества ядер в CPU (рис. 9). Также серьезной доработке подверглась процедура сшивки поверхностей при ее одновременном выполнении несколькими потоками, в результате чего повысился уровень защиты задействованных потоков от несанкционированного доступа к ним.

Остальные доработки коснулись целого ряда функций ядра C3D:

• улучшилось выполнение операции скругления ребер — заметно сократилось число возникающих ошибок и сняты имевшие место ограничения при построении (рис. 10);
• появилась возможность задавать толщину для поверхностей с особыми (полюсными) точками (рис. 11);
• изменился принцип построения ребра жесткости — в случае неудачи делается попытка построения верхней поверхности ребра жесткости в виде поверхности вращения (рис. 12);
• повысилась гладкость сопряжения по касательной поверхностей, построенных по сети кривых (рис. 13).

Ощутимые изменения также произошли в работе двумерных булевых операций (рис. 14). Заказчиком этой работы стала компания ЛЕДАС, активно использующая данную функцию в собственной технологии сравнения геометрии LGC.

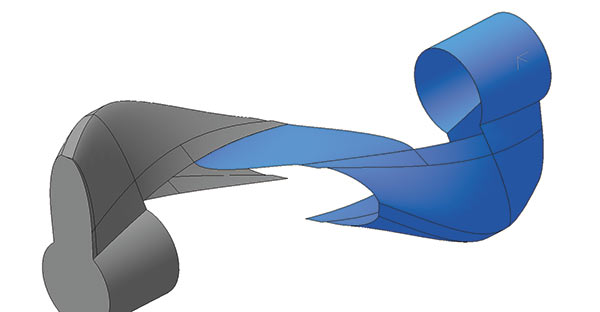
Рис. 13. Улучшенная форма поверхности по сети кривых при задании сопряжений

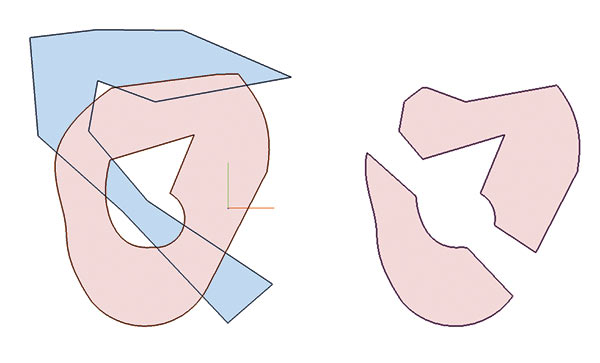
Рис. 14. Работа булевых операций над 2D-объектами

Снимаем ограничения

C3D Labs старается не отставать от современных тенденций и развивает в своем геометрическом ядре параллельное использование всех доступных вычислительных ресурсов, обеспечивая высокую производительность C3D. Специально для этих целей был лицензирован комплекс инструментов для оптимизации программного кода, профилировки и распараллеливания приложений, а также обнаружения ошибок памяти и потоков — Intel С++ Studio. Используя возможности ПО Intel, при разработке C3D удалось достичь ощутимого повышения скорости выполнения функций геометрического ядра.

Рис. 15. Зеркальная симметрия деталей в сборке (симметрия ЛСК)

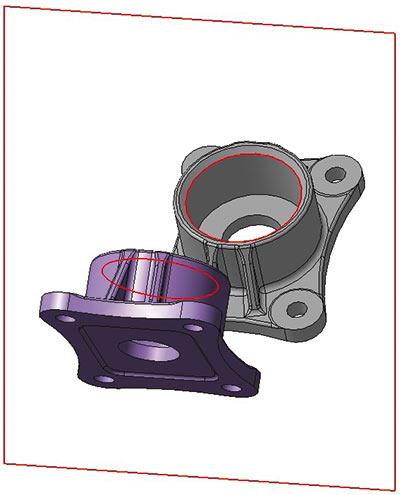
Рис. 16. Зеркальная симметрия по окружностям от пары тел

Рис. 17. Зеркальная симметрия по внешним граням от пары тел

Кроме того, традиционно мы уделяем большое внимание развитию методов и оптимизации математических принципов геометрического оделирования, реализованных в C3D. Работа в этом направлении дает стабильный прирост производительности ядра, сопоставимый с использованием параллельных вычислений. Комплексное же развитие обеих областей позволяет говорить о колоссальных ускорениях в новых версиях C3D, выходящих в свет! В качестве примера такого развития методов задания 3D­моделей приведем новинки решателя C3D. В актуальной версии V16 появился новый тип геометрического объекта — кластер. По сути, это твердое тело, а точнее — геометрически жесткое объединение объектов с собственной подсистемой ограничений. Кластеры могут образовывать иерархии, в которых все подсистемы вычисляются в следующем порядке: снизу вверх от вложенных к содержащим. Подобная организация естественна при конструировании сборок в САПР, предусматривающих разбиение на подсборки. Так, уже не требуется создавать множество экземпляров решателей на каждую подсборку, а достаточно работать с одним решателем, обслуживающим сборку целиком, что приводит к экономии ресурсов и ускоряет вычисления после внесенных изменений в 3D­модель.

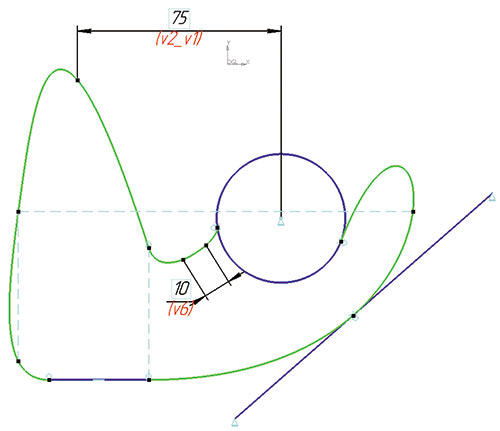
Рис. 18. Интерполяционный сплайн с заданными ограничениями для его контрольных точек

Для удобства разработки приложений также было организовано журналирование в 2D­решателе при задании параметрических ограничений. Журнал представляет собой историю вызовов API геометрического решателя, сохраненную в специальном текстовом файле формата jrn. В этот файл автоматически пишется вся информация о работе C3D Solver с возможностью ее ручного редактирования, что позволяет удаленно отлаживать найденные заказчиками C3D ошибки без учета окружения, в которое встроено ядро. На основе базы журналов реализована система регулярного регрессионного тестирования, осуществляющая проверку каждой рабочей ревизии решателя.

Рис. 19. Модель танка (автор — Сергей Сюваев,
конкурс «МАСТЕР 3D»). Модель содержит 729 различных деталей. На компьютере с четырехъядерным процессором (Intel Core i5) получено сокращение времени импорта: из Parasolid — в 1,7 раза, из STEP — в 2,2 раза

Другая потребность при создании САПР, которой мы уделили внимание в новой версии ядра, — построение симметричных моделей, а именно выполнение 3D­сборок, в которых часть одних деталей полностью или частично является зеркальным отображением других. Такое расположение деталей можно обеспечить новым типом геометрического ограничения — зеркальной симметрией (рис. 15). Зеркальную симметрию можно применить к любым геометрическим объектам, например к окружностям от пары тел или их внешним граням (рис. 16 и 17). В случае если в исходную геометрическую модель будут внесены какие­либо изменения, то симметричные сборки также перестроятся в соответствии с новыми параметрами исходной модели. В рамках работ над зеркальной симметрией, а также для подготовки к плановому расширению функционала была проведена работа по модернизации внутренней архитектуры решателя С3D.

Расширены возможности при построении параметризованных сплайнов:

• доработана функция, которая позволяет манипулировать параметрическим чертежом или эскизом методом drug­and­drop, наблюдая в режиме реального времени изменение формы объектов с сохранением всех заданных ограничений. Такая функция добавляет интерактивности конечно­пользовательскому продукту на основе C3D и называется драггингом;
• значительно улучшено поведение чертежа при драггинге сплайнов или его контрольных точек, а также драггинг геометрических объектов, прямо или косвенно связанных со сплайнами ограничениями;
• добавлена возможность выбора способа построения NURBS­кривых по заданным точкам — появился специальный маркер, определяющий, будет ли сплайн использовать эти точки как опорные данные при построении (полюсные точки) или станет непосредственно проходить через них (интерполяционные точки). На интерполяционный сплайн можно налагать все типы ограничений, которые доступны и для обычной NURBS­кривой (рис. 18);
• появилось новое ограничение, позволяющее задавать форму сплайна путем фиксации координат его отдельных точек или векторов 1­й, 2­й, 3­й производных в точках с заданными параметрами;
• улучшены алгоритмы поддержки ограничений для сплайнов. Это привело к более «естественному» поведению чертежа/эскиза, в частности при наложении касаний со сплайнами. Рассмотрены «сложные» случаи (например, при множественных касаниях);
• реализована функция, которая определяет тип конического сечения, заданного в виде кривой NURBS.

Поддерживаем взаимодействие

Мы понимаем, что каждый разработчик инженерного программного обеспечения желает видеть свой продукт наиболее приспособленным и адаптированным к работе с различными программами, уже представленными на рынке систем автоматизированного проектирования. И поэтому мы произвели ряд улучшений, которые касаются непосредственно модуля C3D, отвечающего за чтение и запись геометрических моделей в различных форматах.

В новой версии конвертора стала доступна настройка точности экспорта STL­моделей по трем параметрам триангуляции: максимальный прогиб, максимальный угол поворота нормали кривой (или поверхности) и максимальная длина стороны треугольника. Все названные параметры могут быть заданы пользователем. Эти доработки необходимы всем нашим заказчикам, работающим с 3D­печатью.

Рис. 20. Импортированная модель в формате STL содержит 2 378 154 вершины и 792 718 треугольников

За счет многопоточности в C3D ускорена конвертация данных при импорте моделей в форматах Parasolid (x_t, x_b) и STEP (рис. 19). Реализован импорт полигональных моделей в форматах STL и VRML (рис. 20). Наконец, появилась поддержка передачи атрибутов со сведениями об изделии (наименование, обозначение, авторство) при конвертации данных.

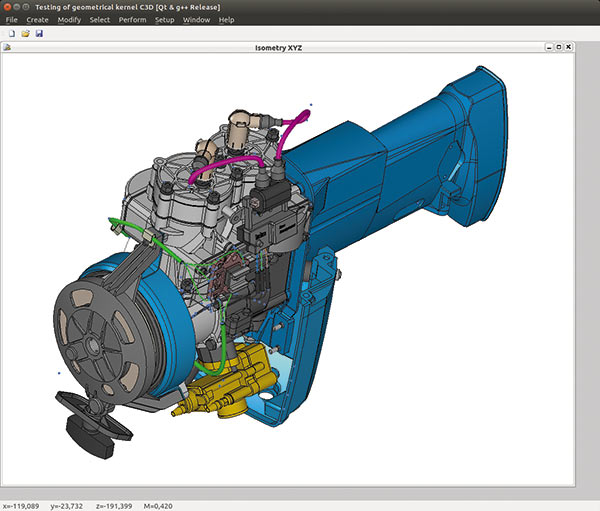
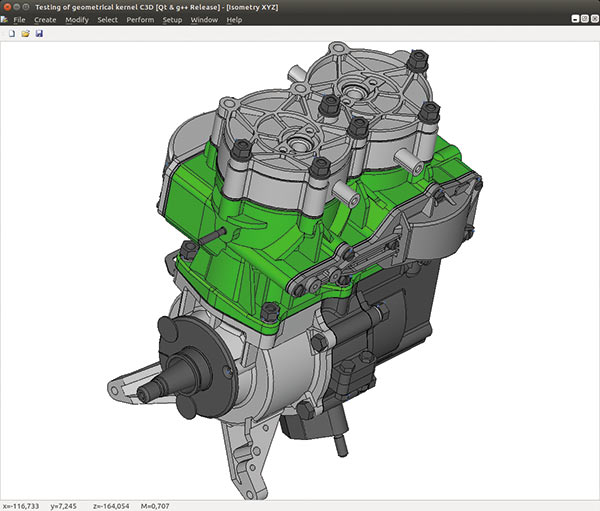
Рис. 21. Тестовое приложение C3D для ОС Linux

Тестируем и развиваем

Сегодня, спустя два года после выхода ядра C3D на рынок, его применяют в своих разработках 15 софт­верных компаний и учебных заведений, и этот список постоянно пополняется. Соответственно, повышаются требования к качеству выпускаемых нами программных компонентов. Специально для системы автоматизированной проверки ревизий C3D мы увеличили число тестовых моделей, на которых отрабатываются функции ядра, до 350 тыс. штук. Каждую ночь мы выполняем миллионы булевых операций! За прошедший год наша команда успела не только разработать более ста новых фич, но и поправила внушительное количество багов, без которых, конечно, никуда. Буквально перед выпуском новой версии C3D мы завершили глубокую переработку тестового приложения для Linux, которое получило обновленный интерфейс и стало гораздо более стабильным (рис. 21).

В процессе модернизации геометрического ядра большую роль играет наличие обратной связи от десятков тысяч тестировщиков — пользователей инженерного программного обеспечения, созданного на базе C3D. Они предоставляют нам ценнейшую информацию — пищу для размышлений и руководство к действию. В процессе такого взаимодействия рождается множество «невидимых» задач по адаптации ПО к запросам пользователей и реформации уже написанного кода в C3D. Но есть и вполне ощутимые запросы по изменению ядра. Специально для разработчиков и для всех будущих заказчиков компании была реализована сборка геометрического ядра C3D компиляторами CLang 3.5 и Visual Studio 2013 и расширен набор поддерживаемых сборок Linux. А самое главное (мы знаем, как долго вы этого ждали!) — начиная с версии V16 разработчики смогут использовать в работе с ядром язык программирования C#, который приобретает огромную популярность среди наших пользователей. Ну, а для тех, кто только начинает изучать геометрическое моделирование, мы разработали иллюстрированное руководство пользователя по ядру.

C3D V16 — это современный инструмент для профессиональной разработки софта и комплексной интеграции геометрических моделей в инженерное программное обеспечение. Используя наши технологии сегодня, вы обеспечиваете устойчивое развитие и стабильную работу вашего программного обеспечения завтра! 

САПР и графика 12`2014