Обратные связи — основа систем, проектирующих трассы дорог

Валерий Струченков

Введение

Традиционно трасса дороги представляется в виде двух плоских кривых: план и продольный профиль. План трассы — это ее проекция на плоскость XOY, а продольный профиль — зависимость координаты Z от длины кривой в плане.

И план, и продольный профиль трассы состоят из элементов, в качестве которых используются отрезки прямых и дуги окружностей, парабол, клотоид и др.

На положение трассы на местности влияют рельеф земли, геологические, гидрологические, климатические условия и другие факторы, в том числе условия землепользования. Проектирование трассы взаимосвязано с решением других проектных задач: проектирование поперечных профилей земляного полотна, проектирование искусственных сооружений (мосты, тоннели, водопропускные трубы и др.), распределение земляных масс, выбор способов производства работ и др.

Известно, что в одних и тех же условиях, располагая одной и той же информацией, не нарушая действующих СНиП, разные специалисты предлагают различные решения не только по вариантам трассы, но в условиях пересеченного рельефа и по вариантам проектной линии продольного профиля при заданном плане трассы.

Экспериментально этот факт на конкретных примерах проектирования продольного профиля автодорог с участием проектантов из различных организаций установил старший научный сотрудник ГипродорНИИ Ю.С. Карих еще в 1976 году [1, 2]. Характерно, что предложенные разными специалистами варианты существенно различались как по геометрии, так и по экономическим показателям [1].

В настоящее время сложившийся за долгие годы подход к проектированию дорог остался в основном таким же, что и в ХIX веке: вариант трассы назначается проектантом, то есть план и продольный профиль вырабатываются на основе опыта и интуиции специалиста до решения всех остальных проектных задач. В дальнейшем на основе полученного проектного решения (план и продольный профиль) другими специалистами проектируется земляное полотно, искусственные сооружения, распределяются земляные массы, выбираются способы производства работ и решаются другие задачи. При этом план и продольный профиль, как правило, не корректируются по результатам решения перечисленных проектных задач. Другими словами, обратная связь если и возникает, то только при обнаружении трудностей в решении какой­либо проектной задачи без изменения положения трассы. Подобная технология (далее для простоты она называется линейной) по самому смыслу задачи не может обеспечить нахождение оптимальных решений по таким критериям, как строительная стоимость или приведенные строительно­эксплуатационные затраты.

В связи с этим еще в 70­х годах прошлого века в СССР были разработаны математические модели, алгоритмы и программы проектирования продольного профиля железных и автомобильных дорог (системы «Профиль» и «Профиль 2А» соответственно). Несмотря на крайне ограниченные возможности ЭВМ того времени, они получили широкое практическое применение. Так, с использованием системы «Профиль» институтами Мосгипротранс, Ленгипротранс и Сибгипротранс только по вариантам трассы БАМ было запроектировано более 1200 км особо сложных участков продольного профиля на ЭВМ БЭСМ­4 (объем оперативной памяти — от 4096 до 8192 ячеек по 45 двоичных разрядов каждая, быстродействие — 40 тыс. операций в секунду). Была подтверждена высокая экономическая эффективность применения математических методов оптимизации при проектировании в условиях пересеченного рельефа железных [3, 4] и автомобильных дорог [5]. Конкретные примеры машинного проектирования продольного профиля приведены в книге [4].

В дальнейшем были разработаны модели, алгоритмы и программы оптимизации плана трассы новых железных дорог на участках подъема и спуска предельными уклонами (участки напряженного хода с автоматическим определением отметок верхней и нижних точек). Установлено, что совместное проектирование плана и продольного профиля дает снижение строительных затрат в несколько раз больше, чем оптимизация продольного профиля при заданном плане трассы [6]. В 1990­х годах эти исследования и разработки были прекращены, а программы утрачены.

В настоящее время при наличии мощной вычислительной техники с богатейшими возможностями визуализации информации, организации интерактивного режима работы, изготовления документации и др., а также при значительных успехах теории системного анализа, математического моделирования, теории оптимизации есть все возможности создания новой технологии проектирования оптимальных трасс линейных сооружений, в которой комплекс взаимосвязанных проектных задач рассматривается совместно. Однако получившие широкое распространение современные САПР, разработанные западными фирмами [7, 8, 9],
и их российские аналоги [10] ориентированы на всё ту же линейную технологию.

Цель настоящей статьи заключается в том, чтобы проанализировать процесс выработки проектных решений в действующих САПР и изложить другой подход, основанный на использовании обратных связей в проектирующих системах, в которых ключевые проектные решения вырабатываются не проектантом, а компьютером на основе комплексных математических моделей и математических алгоритмов оптимизации. Такой подход характерен при создании нового поколения САПР — интеллектуальных систем (Intelligence Systems).

Интерактивное проектирование в САПР

В современных САПР в интерактивном режиме проектант по своему усмотрению может последовательно подбирать и увязывать элементы проектируемой линии (плана или продольного профиля), назначая параметры элементов или другие данные, обеспечивающие их полный и однозначный расчет. Компьютер выполняет расчет элементов, их визуализацию и корректировку по требованию проектанта. Для подобного crawling on the screen не имеют значения особенности проектной задачи, отсюда и универсальность подобных систем, в которых компьютер решает простейшие расчетные задачи типа «вписать кривую в угол» и не ориентирован на поиск оптимальных решений сложных проектных задач, например совместное проектирование продольного и поперечных профилей земляного полотна будущей дороги. По образному выражению одного из специалистов, успевшего поработать с системой «Профиль», проектирование профиля в современных САПР — это возврат к ручному труду с новыми инструментами. Техническое совершенство этих инструментов не отменяет истинности приведенного высказывания.

Сложился и многими специалистами упорно поддерживается миф о том, что crawling on the screen дает оптимальные проектные решения при проектировании дорожных трасс. Так, в статье «Быстрое макетирование инфраструктурных моделей с помощью Autodesk InfraWorks» [11] читаем: «При использовании Autodesk InfraWorks на вооружении у проектировщика имеется большой набор эффективных инструментов. Например, инструменты для проектирования дорог позволяют создать оптимальный профиль дороги с учетом стоимости строительства в данной местности. Есть возможность вписывания кривых, переходных кривых, редактирования дороги на профиле и в 3D».

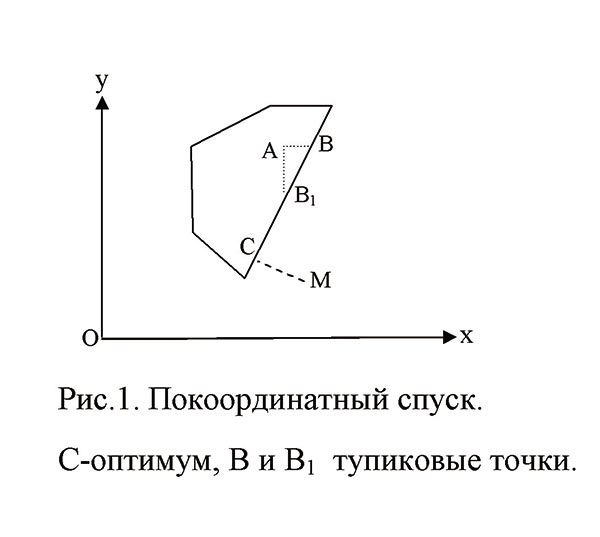
Покоординатный спуск. С-оптимум, В и В1 тупиковые точки

Уместно заметить, что возможность вписывания круговых и переходных кривых имелась у русских инженеров еще во времена Гарина­Михайловского, правда на бумаге, а не на экране компьютера, но при чем здесь оптимизация? Кстати, в Autodesk InfraWorks нет возможности вычислить параметры переходной кривой (клотоиды), аппроксимирующей заданную систему точек на плоскости из условия минимума суммы квадратов отклонений от этих точек. А в нашей стране еще в 1980­х годах прошлого века с применением алгоритма нелинейного программирования была решена на ЭВМ ЕС задача аппроксимации системы точек не одиночной клотоидой, а системой: прямая, клотоида, окружность, клотоида, прямая и т.д. [12]. При решении этой задачи, возникающей при проектировании плана трассы реконструируемой железной дороги, положение всех элементов трассы на перегоне оптимизировалось совместно [12]. Элементы аппроксимирующей кривой взаимосвязаны, так как в точках сопряжения они должны иметь не только общую касательную, но и общую кривизну. При последовательном поэлементном проектировании плана трассы дороги эта взаимосвязь учитывается не в полной мере. При фиксации на экране очередного элемента (пусть даже оптимальным образом) сужаются возможности варьирования для следующего элемента и т.д. В результате, дойдя до последнего элемента при фиксированных конечной точке и направлении, проектант практически имеет один вариант положения последнего элемента. Но если начать процесс с последнего элемента и двигаться справа налево, то на первом шаге будет много возможных вариантов, а на последнем — нет. Соответственно нет оснований утверждать, что будет получена оптимальная линия при crawling on the screen. Этот процесс напоминает известный в математике метод минимизации функции многих переменных, который называется «покоординатный спуск» [13]. Он состоит в поочередной минимизации по отдельным переменным и может успешно работать при отсутствии взаимосвязи переменных, но непригоден при решении задач, в которых такая взаимосвязь есть. В проектировании дорожных трасс, в том числе в рассматриваемой простейшей задаче среднеквадратической аппроксимации последовательности точек на плоскости, имеет место именно такая взаимосвязь [14].

Иллюстрацией сказанного может служить ситуация, представленная рисунке, где переменными являются x и y, ограничения формируют допустимую область и требуется найти в этой области точку, ближайшую к заданной точке M. Из начальной точки А, меняя только одну переменную, получаем точку В или В1, в зависимости от того, какую координату меняем первой. Обе эти точки являются тупиковыми, так как изменение только одной координаты x или y выводит за пределы допустимой области или увеличивает расстояние от точки M. При этом очевидно, что решением задачи является точка С, в которую из точки B или В1 без нарушения ограничений и без увеличения значения целевой функции можно попасть только при одновременном изменении двух переменных.

В случае минимизации функций многих переменных в многомерных пространствах при наличии сложных ограничений такая тупиковая ситуация может возникнуть при одновременном изменении целой группы переменных. Поэтому нет оснований для утверждений о получении оптимальных решений при crawling on the screen.

Если ставится цель поиска оптимальных решений, то в задачах проектирования плана и продольного профиля дорог искомая линия должна рассматриваться как единое целое [15].

Относительно создания оптимального профиля дороги с учетом стоимости строительства в данной местности при использовании Autodesk InfraWorks [11] также возникают сомнения. Действительно, стоимость строительства невозможно учесть и даже просто вычислить, если не запроектировано земляное полотно, искусственные сооружения, не распределены земляные массы, не выбраны способы производства работ и др. Представляется очевидным, что возможность вписывания кривых и редактирование дороги на профиле и в 3D если и способствуют, то никак не гарантируют создание оптимального профиля дороги и не имеют прямого отношения к снижению стоимости строительства. Кстати, возможность редактирования продольного профиля дороги была реализована в дополнительных блоках упомянутых систем «Профиль» и «Профиль­2А» при появлении в нашей стране ПЭВМ IBM PC AT­260 [16]. И было это более 20 лет тому назад.

Большой набор эффективных инструментов, в особенности 3D­модели, в Autodesk InfraWorks — это безусловное благо, но он не избавляет проектанта от crawling on the screen, не позволяет автоматизировать творческие процессы выработки проектных решений. Поэтому подобные системы нельзя отнести к современным интеллектуальным системам (Intelligence Systems), и с этой точки зрения они, при всем обилии эффективных инструментов, — безусловно, шаг назад по сравнению с отечественными разработками по оптимизации дорожных трасс, выполненными до разгрома прикладной науки в России в 1990­х годах [16].

Проектирующие системы с обратными связями

Реализация идеи компьютерного проектирования трассы как пространственной кривой наталкивается на существенные трудности как в формализации задачи, так и в применении математически корректных алгоритмов. В реальной постановке задача оказывается многоэкстремальной [17], а для решения такого класса задач современная теория не дает надежных методов поиска глобального экстремума.

К настоящему времени разработаны модели и алгоритмы проектирования трассы новой дороги как пространственной кривой в заданной полосе варьирования на основе оптимизации варианта, запроектированного вручную [17].

На программную реализацию этих алгоритмов в ближайшее время рассчитывать не приходится, ибо можно создать модели и алгоритмы в порядке творческой инициативы одного человека, но разработка сложных комплексов программ требует усилий коллектива специалистов и соответствующего финансирования.

В связи с этим автором в среде C++ BUILDER реализованы только две проектирующие системы с компьютерной выработкой проектных решений на основе математических моделей и алгоритмов оптимального проектирования. Подчеркнем: речь идет не об оптимизации (то есть улучшении) некоторого имеющегося решения, а о выработке оптимального решения системой «с нуля». Разного рода эвристические алгоритмы «генерирования оптимальных решений» не рассматриваются.

САПР «Трасса ж.д.»

Эта система предназначена для проектирования трасс новых железных дорог. В стадии разработки находится аналогичная система для проектирования трасс новых автомобильных дорог.

 В САПР «Трасса ж.д.» выполняется совместное проектирование продольного и поперечных профилей земляного полотна по вариантам плана трассы новой железной дороги по критерию минимума строительных затрат.

На первом этапе исходными данными являются: план трассы, продольный и поперечные профили земли, нормы проектирования и высотные ограничения. По этим данным компьютер проектирует продольный профиль по критерию минимума объемов земляных работ в расчете на «стандартные» поперечные профили земляного полотна, то есть насыпь шириной на уровне профильной бровки 7 м и выемка — 12 м, показатель крутизны откосов — 1,5. Далее компьютер проектирует поперечные профили на каждом пикете и плюсе с использованием библиотеки типовых правил (алгоритмов) проектирования откосов насыпей и выемок. Библиотека доступна для визуального анализа, но проектант должен указать номера типовых алгоритмов для насыпей и выемок применительно к различным участкам профиля.

На каждом переломе профиля земли проектирование поперечных профилей выполняется многократно с заданным шагом относительно имеющейся проектной линии. В итоге вычисляются параметры зависимостей площадей насыпей и выемок от рабочих отметок в заданном диапазоне относительно этой линии. Рабочие отметки вычисляются как разность проектных отметок и отметок земли по оси трассы.

Если задана геология, то такие зависимости строятся компьютером отдельно для каждого слоя. Именно эти зависимости являются основой для корректировки проектной линии компьютером. Результат корректировки используется как основа для уточнения упомянутых зависимостей при сужении области поиска и уменьшении шага изменения рабочих отметок.

Проектант имеет возможность проанализировать продольный и поперечные профили, запроектированные компьютером, при необходимости внести коррективы в исходные данные и повторить расчет или перейти к следующему этапу, на котором проектирование выполняется не по минимуму объемов земляных работ, а по стоимостному критерию. Для этого компьютеру нужно задать затраты в расчете на 1 м3 по видам земляных работ: сооружение насыпей из грунта выемок, сооружение насыпей из привозного грунта, разработка в отвал ненужного или непригодного для сооружения насыпей грунта выемок. Все грунты по возможности использования для сооружения насыпей делятся на следующие типы: непригодные, обыкновенные, дренирующие нескальные, скальные. Для грунтов различных типов единичные стоимости могут различаться. Задание геологии осуществляется указанием шифров из имеющихся в системе библиотеки грунтов (около ста наименований) и отметок подошв слоев грунта. При использовании грунтов выемок для сооружения насыпей задание упомянутых единичных стоимостей должно выполняться после распределения земляных масс и выбора способов производства работ [17].

Дальнейшая корректировка продольного профиля осуществляется компьютером с использованием стоимостных зависимостей по каждому типу грунтов на каждом переломе профиля земли. Зависимости строятся компьютером аналогично построению зависимостей площадей от рабочих отметок [17]. Расчеты могут повторяться при уточнении данных для очередной корректировки проектной линии.

Искусственные сооружения учитываются при задании для каждого из них зависимости его стоимости от рабочей отметки. Выбор типов сооружений и задание соответствующих им зависимостей должны осуществляться после расчета стока из малых бассейнов. При каждом новом поступлении информации компьютер корректирует проектную линию, в чем, собственно, и состоит обратная связь.

Управление процессом остается за проектантом, как и принятие окончательного решения. В частности, если проектирование продольного профиля выполняется для выбора одного из заданных вариантов плана трассы, то эти варианты могут сравниваться при параллельном выполнении расчетов продольного профиля, и проектант может принять решение об отбраковке неконкурентных вариантов еще до полного завершения расчетов. Естественно, что для такого сравнения должны вычисляться строительные затраты, пропорциональные длине трассы, и эксплуатационные расходы, которые в целевую функцию при оптимизации профиля не включались.

В условиях равнинного рельефа компьютер проектирует продольный профиль насыпью, высота которой определяется требованиями защиты дороги от снежных заносов. Расчеты выполняются однократно по каждому варианту плана трассы.

В САПР «Трасса ж.д.» процесс выработки проектного решения остается интерактивным, но компьютер становится, в некотором смысле, интеллектуальным партнером, который может «сметь своё суждение иметь».

САПР «Реконструкция трасс ж.д.»

Эта система предназначена для проектирования плана и продольного профиля при реконструкции железных дорог, их капитальном ремонте или выправке пути.

Проектирование плана трассы осуществляется по критерию взвешенной суммы квадратов сдвижек относительно существующего пути.

Весовые коэффициенты в целевой функции пропорциональны абсолютным величинам рабочих отметок в профиле.

Проектирование плана трассы выполняется в два этапа:

• построение начального приближения, то есть определение числа и последовательности элементов, удовлетворяющих заданным техническим требованиям;
• оптимизация параметров элементов с соблюдением всех ограничений или выявлением невозможности сделать это в силу противоречивости ограничений.

Оптимизация выполняется по DFP­методу с использованием модифицированной функции Лагранжа [18]. Характерной особенностью алгоритма является возможность получения целочисленных значений радиусов круговых кривых и/или длин переходных кривых, кратных 10 или 5 м. Другая важная особенность алгоритма состоит в недопущении попадания переходных кривых в запрещнные зоны, например на мосты без балласта.

Продольный профиль в САПР «Реконструкция трасс ж.д.» также проектируется по новому методу, который является комбинацией нелинейного и динамического программирования [17].

В системе есть средства визуализации, анализа и при необходимости корректировки не только исходных данных, но и компьютерных проектных решений, а также средства контроля вносимых проектантом корректировок на предмет их непротиворечивости исходным данным для проектирующих программ.

Заключение

Рассмотренные системы с обратными связями в существующем виде могут использоваться в проектной практике. Однако возможности их развития и совершенствования далеко не исчерпаны. В частности, для эффективного применения САПР «Трасса ж.д.» на всех стадиях разработки проекта новой железной дороги она должна быть дополнена следующими блоками (подсистемами):

• распределения земляных масс и выбора способов производства работ;
• расчета стока и назначения типов малых искусственных сооружений. Целесообразно создание библиотеки таких сооружений, содержащей их параметры и соответствующие стоимостные зависимости.

Необходимо подчеркнуть, что речь не идет о пресловутом «импортозамещении», так как проще оснастить действующие САПР блоками компьютерной выработки проектных решений и реализовать технологию проектирования дорожных трасс с обратными связями вместо crawling on the screen.

На пути создания интеллектуальных систем в данной области имеется много препятствий, из которых главное — это отсутствие инстанций, реально заинтересованных в повышении качества проектов, в снижении затрат труда и средств в строительстве. 10­15% снижения затрат при строительстве дорогостоящих дорог окажутся нелишними, когда цель «освоения» средств сменится целью их экономии. В ближайшее время на это рассчитывать не приходится.

В создании подобных систем не заинтересованы и фирмы — разработчики САПР, поддерживающие миф об оптимальности решений при crawling on the screen.

В реальности этого мифа некоторые пользователи уже убедились при сопоставлении их решений с решениями, получаемыми с помощью проектирующих программ. Автор предлагает и другим пользователям убедиться в этом, в частности на примере решения вышеупомянутой задачи аппроксимации, к которой сводится проектирование плана трассы реконструируемой железной дороги.

Будущее — за проектирующими программами и интеллектуальными системами. 

Список литературы:

1. Карих Ю.С. Оценка существующих методов проектирования продольного профиля. В сб. трудов ГипродорНИИ № 17. Повышение экономической эффективности капиталовложений в строительство, ремонт и содержание автомобильных дорог. М.: Издание ГипродорНИИ, 1976.
2. Струченков В.И. О методологии компьютерного проектирования трасс линейных сооружений // САПР и графика. 2013. № 7.
3. Космин В.В., Струченков В.И., Фрадков Е.Б. Проектирование продольного профиля дороги на ЭВМ // Транспортное строительство. 1971. № 4.
4. Использование математических методов оптимизации и ЭВМ при проектировании продольного профиля железных дорог. Труды Всесоюзного НИИ транспортного строительства. Вып. 101. М: Транспорт, 1977.
5. Струченков В.И., Карих Ю.С., Шварц П.С. Математические методы оптимизации в системе автоматизированного проектирования дорог // Автомобильные дороги. 1980. № 12.
6. Струченков В.И., Шейдвассер Д.М. Оптимизация на ЭВМ трассы новой железной дороги на напряженных ходах // Транспортное строительство. 1987. № 3.
7. CARD/1. http://www.card­1.com/en/home/
8. Bentley Rail Track. http://www.bentley.com/
9. http://www.autodesk.ru/products/infraworks­family/features/civil­engineering­design/gallery­view
10. Тоpomatic Robur. http:// www.topomatic.ru
11. Юсупова А., Берзин Э. Быстрое макетирование инфраструктурных моделей с помощью Autodesk InfraWorks // САПР и графика. 2014. № 3.
12. Носков А.В., Струченков В.И., Шейдвассер Д.М. Проектирование плана трассы при реконструкции ж.д. // Транспортное строительство. 1990. № 3.
13. Аоки М. Введение в методы оптимизации: Пер. с англ. М.: Наука,1977.
14. Struchenkov V.I. Mathematical Models and Optimization in Line Structure Routing: Survey and Advanced Results // International Journal Communication, Network and System Sciences. Special Issue: Models and Algorithms for Application. 2012. № 5.
15. Struchenkov V.I. Nonlinear Programming Algorithm for CAD Systems of Line Structure Routing // World Journal of Computer Application & Technology, Horizon Science Publisher, vol. 2. 2014. № 5.
16. Струченков В.И. Методы оптимизации в проектировании трасс линейных сооружений // Сб. научных трудов. Искусственный интеллект в технических системах. Вып. № 20. М.: Гос. ИФТП,1999.
17. Струченков В.И. Методы оптимизации трасс в САПР линейных сооружений. М: Солон­Пресс, 2014.
18. Гилл Ф., Мюррей У, Райт М. Практическая оптимизация. Пер. с англ. М: Мир,1985. 

САПР и графика 1`2015