Оживляя механизмы. Работа с анимацией в системе автоматизированного проектирования КОМПАС-3D (часть 3). Переменные

Михаил Паньков,
инженер-технолог 1-й категории отделения разработки управляющих программ для станков с ЧПУ,
НИИЦ (г.Курск) ФГУП «18 ЦНИИ» МО РФ

Разобравшись во второй части статьи с простыми моментами, связанными с использованием управляющих переменных в качестве альтернативных способов движений вращения и перемещения в процессе анимации, можно перейти к более сложным методам анимации, а именно — к использованию функций.

Их применение рассмотрим на примере чеканочного пресса (пример взят из тематического задания личного зачета очного этапа олимпиады CAD­OLYMP 2013). Кинематическая схема станка (рис. 1) предполагает перемещение рычага 2 за счет вращения шестерни 1. В отличие от шестерни, рычаг 2 имеет зубчатый венец внутреннего зацепления.

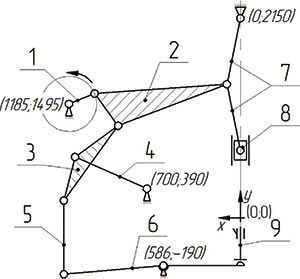
Рис. 1. Кинематическая схема чеканочного пресса

Рычаг совершает возвратно­поступательные движения за счет перемещения его узловой точки, которая находится в центре зубчатого венца, по делительной окружности. Анимацию движения точки по окружности можно задать как перемещение объекта по траектории. Усложним задачу, чтобы рассмотреть использование функций для применения в анимации. Из курса высшей математики известно, что координаты точки окружности с заданным радиусом в полярной системе координат находятся по формулам:

X = X0xRxcos(t);

Y = Y0xRxsin(t),

где X0 и Y0 — это координаты центра окружности; R — радиус окружности; t — угол.

Если центр окружности находится в центре системы координат, то X0 и Y0 равны нулю. В нашем случае (рис. 1) центр окружности имеет координаты X0=1185; Y0=1495. Эти координаты соответствуют центру шестерни, поэтому построим ось на пересечении двух плоскостей. Одна плоскость будет смещена от плоскости YZ на величину 1185 — это переменная X0, а другая плоскость будет ей перпендикулярна и смещена относительно плоскости XZ на величину 1495 — это переменная Y0. Радиус окружности R в окне переменных можно представить как выражение 255/2 или 127.5 — система примет в расчет и тот и другой вариант.

Переменные X и Y отвечают за положение точки в определенный момент угла t. Угол t — это угол между начальным и конечным положениями точки относительно центра окружности. Для удобства написания сценария и наложения сопряжений на взаимосвязанные элементы начало отсчета перемещения точки рычага 2 возьмем на горизонтальной оси, проходящей через центр шестерни в точке, при которой угол t=0°. Это положение рычага фиксируем сопряжением Расстояние относительно нулевых координат X и Y. В окне переменных, в разделе Сопряжения, находим только что построенные сопряжения, и соответствующим параметрам присваиваем пользовательские переменные X и Y. Они автоматически появляются в главном разделе с присвоенными численными значениями. В поле Выражение вместо числа переменной X укажем функцию X(t). Система автоматически сгенерирует в главном разделе подраздел Функции, в одном из полей которых будет указана переменная X(t) на бирюзовом фоне. В соответствующем этой функции поле Выражение запишем условие функции X = X0xRxcos(t). Как только выражение будет записано и нажата клавиша Enter, система сгенерирует в главном разделе переменную t, которой до этого не было в списке. Полный оборот точки вокруг центра составляет 360°, что в пересчете на радианы равно 2p. В синтаксисе КОМПАС­3D присутствует константа, отвечающая за число p — это M_PI. Неудобство ее подстановки вместо значения переменной заключается в том, что переменной t ее присвоить можно, а в библиотеке анимации в качестве границы диапазона — нельзя. Поэтому число p заменяем числом 3,1415925, а полный оборот будет в два раза больше — 6,283185 радиана. Аналогичные манипуляции производятся с функцией Y(t) (рис. 2).

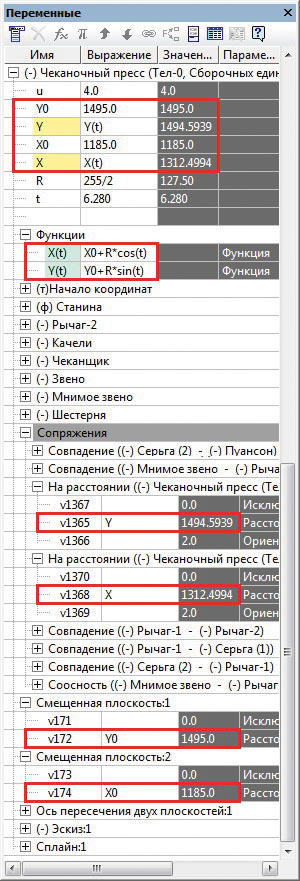
Рис. 2. Создание функций в окне переменных

Для того чтобы создать эффект зубчатого зацепления, необходимо шестерню разметить под углом к рычагу методом подбора так, чтобы зуб шестерни был во впадине зубчатого венца рычага. Это делается сопряжением Под углом, при этом метод подбора легко осуществлять, если углу присвоена переменная. Когда будет создаваться анимация, это сопряжение необходимо отключить, потому что за зубчатое зацепление будет отвечать уже знакомый тип механического сопряжения компонентов Вращение­вращение. Для данного примера такое сопряжение работать не будет, поэтому необходимо прибегнуть к определенной хитрости:

1. В шестерне создается цилинд­рическая поверхность диамет­ром, равным делительному диаметру шестерни, а именно 127,5 мм.
2. Создается мнимая деталь, в которой строится цилиндричес­кая поверхность диаметром, равным делительному диаметру зубчатого венца рычага, — 255 мм.
3. Между рычагом и мнимой деталью в сборке накладывается сопряжение Соосность их центральных осей, а также Совпадение взаимно перпендикулярных плоскостей (рис. 3).

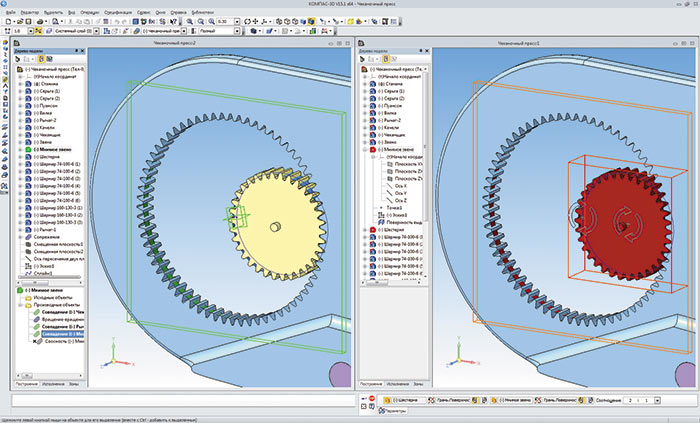
Рис. 3. Создание мнимой детали для достижения результата зубчатого зацепления

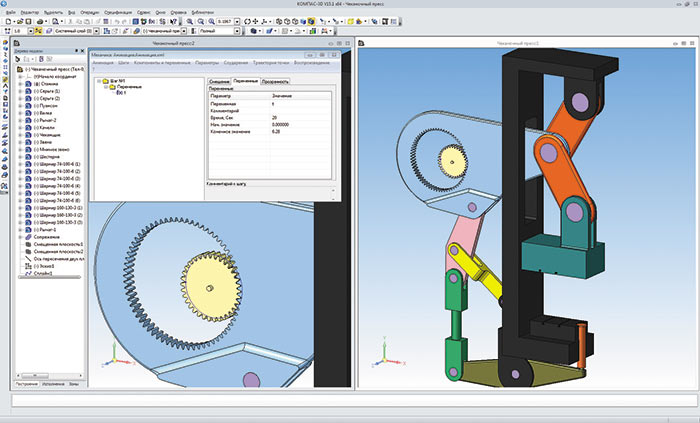
Рис. 4. Анимация чеканочного пресса

Сопряжение Вращение­вращение накладывается между двумя цилиндрическими поверхностями. Так как система видит диаметры цилиндров, в диалоге выбора она автоматически предлагает передаточное отношение, при котором элементы будут совершать перемещения друг относительно друга. Остается лишь выбрать направление вращения этих элементов и запустить сценарий анимации. Как уже говорилось, угол, который был нужен для правильного визуального восприятия попадания зуба шестерни во впадину рычага, отключаем — тем самым мы расфиксируем шестерню. В проекте анимации присутствуют всего один шаг и одна переменная, которая отвечает за изменение переменной t (рис. 4).

Логика, заложенная в системе КОМПАС­3D, тоже имеет место быть, и следующий пример связан именно с ней. Все логические операторы, которые могут быть применены в окне переменных, приведены в приложении IV таблица 2 встроенной справки Компас­3D. Рассмотрим логику на примере анимации часов (пример взят из тематического задания регионального этапа олимпиады CAD­OLYMP 2014). В задании требуется построить недостающие элементы согласно прилагаемым чертежам, а также собрать механизм. Создавать анимацию в данном случае не требовалось, однако данный пример может наглядно продемонстрировать применение логики. Особо сложных моментов в привязке управляющих переменных к стрелкам часов нет. Как и в предыдущих примерах, здесь использовалось сопряжение Под углом с типом угла «2D» относительно оси центра циферблата. Выставим через «u_hour» и «u_min» переменные, которые отвечают за расчет часовой и минутной стрелки, и выведем формулы. В одном часе 60 минут, следовательно, дискретность шага минутной стрелки — это ее поворот на 6°. В циферблате всего 12 часов, после чего часовая стрелка идет на второй круг, следовательно, дискретность шага часовой стрелки — это ее поворот на 30°. Учитывая, что при ходе минутной стрелки часовая тоже двигается, а именно на половину хода минутной стрелки, то можно вывести формулу для расчета угла поворота как часовой, так и минутной стрелки. Выразим значение часовой стрелки через t1, а значение минутной — через t2, тогда формула изменения угла будет такой:

u_hour = y+t1x30+t2x0,5 — для часовой стрелки;

u_min = y+t2x6 — для минутной стрелки.

В найденных формулах y — это постоянная величина, отсчитывающая нулевой рубеж времени (0:00). Стрелки на часах показывают время в соответствии с введенными значениями в поля переменных t1 и t2.

Добавим нашим часам немного модерна и сделаем в циферблате окошко, в котором будет красоваться надпись «AM/PM» («до полудня/после полудня»). Логика в этом примере будет связана с данной надписью. Когда часовая стрелка перевалит за 12 часов дня, надпись в окошке сменится с «AM» на «PM». Надпись делается с двух противоположных сторон на цилиндре, чтобы была возможность его поворота за счет сопряжения «Под углом». Это логическое выражение можно сформулировать следующим образом: «Если часовая стрелка t1 < 12 часов, то надпись AM (цилиндр остается на месте), иначе надпись PM (цилиндр вращается на 180°)». В синтаксисе КОМПАС­3D это будет выглядеть иначе:
(t1 < 12) ? 0,1 : 180,1 (рис. 5).

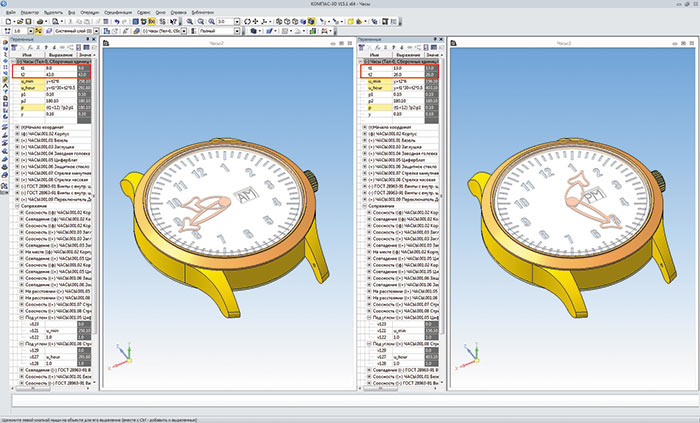
Рис. 5. Результат настройки часового механизма и переменных

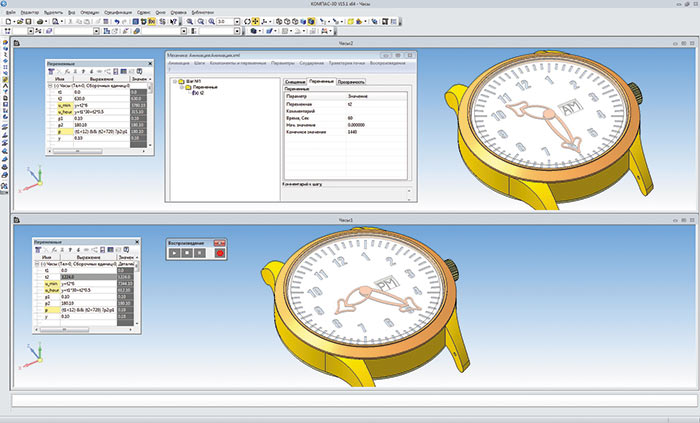
Рис. 6. Время вперед!

Для реализации анимации создадим эффект безостановочного вращения стрелок. Для этого понадобится изменение всего одной переменной, а именно t2, которая отвечает за минутную стрелку. Так как в одном часе 60 минут, а в сутках 24 часа, то диапазон изменения величины t2 будет [0;1440]. Единственный нюанс заключается в следующем: логическое выражение в примере выше было завязано на переменную t1, которая в режиме анимации отсутствует. Чтобы не менять ничего в примере, можно немного преобразовать формулу, которая не повлияет на работу механизма. Среднее значение диапазона изменения величины t2, равное 720 минутам, — это переход момента времени с «до полудня» на «после полудня». Поэтому формула примет вид: (t1 < 12) && (t2 < 720) ? 0,1 : 180,1 (рис. 6), где && — в выражениях логики частица «ИЛИ». Сценарий анимации включает всего один шаг с одной переменной.

Для более полного закрепления материала работы с переменными остановимся на одном из полезных инструментов при работе с переменными — таблице переменных. Это таблица, которая хранится в файле Excel и содержит определенные значения переменных данного файла. Таблица переменных формируется пользователем во время создания или редактирования файла, имеющего внешние переменные. Впоследствии таблица может быть отредактирована или удалена из файла. Таблица переменных выглядит следующим образом:

• первая строка, начиная со второй ячейки, содержит имена переменных;
• первый столбец, начиная со второй ячейки, содержит комментарии к строкам;
• остальные ячейки содержат значения внешних переменных (рис. 7).

Работа с таблицами переменных удобна, когда деталь имеет несколько исполнений (унификация), или для реализации базы стандартных элементов. Мало кто знает, что таблицу переменных можно использовать для поиска оптимального решения в оптимизационных задачах.

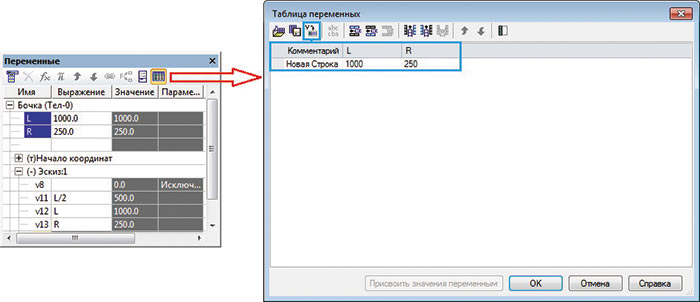
Рис. 7. Вызов таблицы внешних переменных

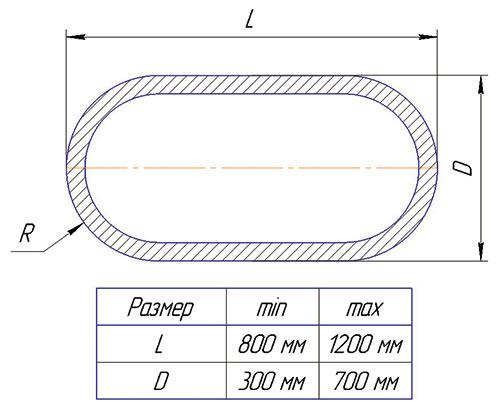
Рис. 8. Чертеж бочки и диапазон изменения параметров

Решим оптимизационную задачу на примере бочки, немного упростив ее, чтобы не вдаваться в подробности выведения сложных формул (пример взят из тематического задания­аналога личного зачета очного этапа олимпиады CAD­OLYMP 2014). Данная задача представляет собой не пример анимации, а пример использования таблицы внешних переменных. В любом случае значения переменных, полученные путем решения таких задач, могут применяться для создания проекта анимации.

Немного отвлечемся от моделирования и расскажем о понятии оптимизации. В своей жизни мы часто сталкиваемся с ситуацией, когда из некоторой совокупности возможных вариантов принятия решения в какой­либо области деятельности необходимо выбрать один вариант. Наилучший вариант поведения (принятие наилучшего решения) можно выбирать по­разному. Если такой выбор преду­сматривает проведение количественного анализа ситуации путем сравнения различных вариантов с помощью какой­либо количественной оценки этих вариантов, то говорят о необходимости решения задачи оптимизации (от лат. optimus — наилучший).

По содержанию задачи оптимизации весьма разнообразны. Они могут быть связаны с проектированием технических устройств и технологических процессов, с распределением ограниченных ресурсов, планированием работы предприятий и т.д. Для решения задачи оптимизации необходимо сформулировать критерий оптимальности, то есть определить те признаки и предпочтения, по которым следует провести сравнительную оценку альтернатив и выбрать среди них наилучшую с точки зрения поставленной цели оптимизации. При этом критерием оптимальности может быть требование достижения наибольшего или наименьшего значения одной или несколькими действительными функциями параметров оптимизации, выражающими количественно меру достижения цели оптимизации рассматриваемого объекта. Каждую из таких функций принято называть целевой.

Для того чтобы добиться улучшения, необходимо располагать математической моделью объекта оптимизации. Эта модель описывает объект при помощи соотношений между величинами, характеризующими его свойства. Обычно хотя бы часть этих величин можно изменять в некоторых пределах, что и порождает множество альтернатив, среди которых и предстоит выбрать наилучшую. Изменяемые при оптимизации величины, входящие в математическую модель объекта оптимизации, называют параметрами оптимизации, а соотношения, устанавливающие пределы возможного изменения этих парамет­ров, — ограничениями, которые могут быть заданы в форме равенств или неравенств.

Геометрия детали «Бочка» должна быть определена путем оптимизации.

Внутренний объем бочки должен быть не меньше 0,3 м3, а вес бочки минимальным. Толщина стенки бочки 5 мм, плотность материала стенки 7800 кг/м3 (7,8x10–6 кг/мм3).

На рис. 8 показана геометрия бочки, а также указан диапазон варьирования размеров при оптимизации.

Для начала необходимо построить параметризованную бочку по размерам, лежащим приблизительно в середине диапазона изменяемых величин. В нашем случае изменениям подвергается длина бочки L и ее радиус R, равный половине диаметра D. Дуга радиуса R касательна в точке перехода в прямой участок и нормальна к оси вращения, поэтому радиус бочки равен радиусу сферы. Весь расчет по нахождению оптимальных параметров бочки сводится в окно программы Excel, но, чтобы правильно сделать расчет, необходимо для начала создать файл с таблицей внешних переменных из диалога системы КОМПАС­3D, а не наоборот. Это будет временный файл с временными значениями переменных, которые будут впоследствии заменены переменными, полученными в ходе расчета.

Создадим таблицу внешних переменных и запишем ее в файл. Для этого надо нажать соответствующую пиктограмму в окне переменных и считать внешние переменные в появившееся окно. После этого сохраняем таблицу в файл Excel. На этом работа в КОМПАС­3D приостанавливается. Для корректного отображения результата в дальнейшем требуется закрыть окно модели.

Открываем только что сохраненную таблицу в программе Excel. В левом верхнем углу окна находится таблица внешних переменных. Чтобы не допустить какой­нибудь ошибки при обратной конвертации в формат КОМПАС­3D, необходимо создать второй лист в одном документе (рис. 9). Во втором листе будет производиться весь расчет оптимизации.

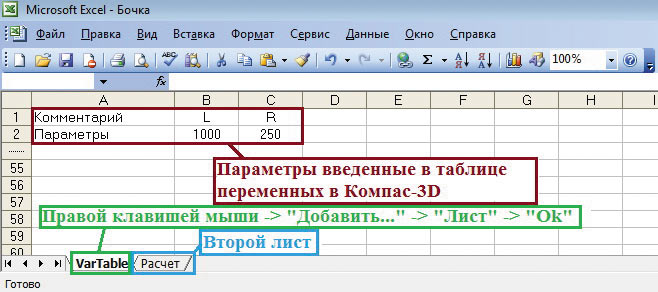
Рис. 9. Открытие таблицы в Excel и создание второго листа

Для того чтобы приступить к нахождению оптимальных параметров бочки, необходимо зайти в меню Сервис -> Надстройки… и из доступных надстроек включить Поиск решения. Теперь эта опция будет активна в меню Сервис -> Поиск решения. Она отвечает за рутинный расчет оптимального решения. Пользователю необходимо только правильно описать формулы, вывести ограничения и записать целевую функцию, а все остальное система сделает сама.

Чтобы выполнить задание, надо знать внутренний объем (пустота) и массу бочки. В КОМПАС­3D, увы, переменные объема или массы не входят в объект «Измерение», поэтому их придется вычислять посредством вывода формулы объема. Бочка является сложным геометрическим телом, поэтому для расчета объема ее необходимо разбить на простейшие тела. Так как края бочки — полусферы, то в совокупности они дадут целую сферу, а в средней части сферы — цилиндр.

Формула расчета объема цилиндра: Vц = Пи x R2 x H;

Формула расчета объема сферы:  ,

где R — радиус бочки; H — высота цилиндра, равная L–2xR.

По условию задания вес бочки должен быть минимальным — это и есть критерий оптимальности. Следовательно, при неизменной плотности материала бочки ее масса будет минимальна при минимальном объеме — целевая функция будет иметь вид:  рxV -> min. К параметрам оптимизации, которые могут изменяться, относится радиус R бочки и ее длина L.

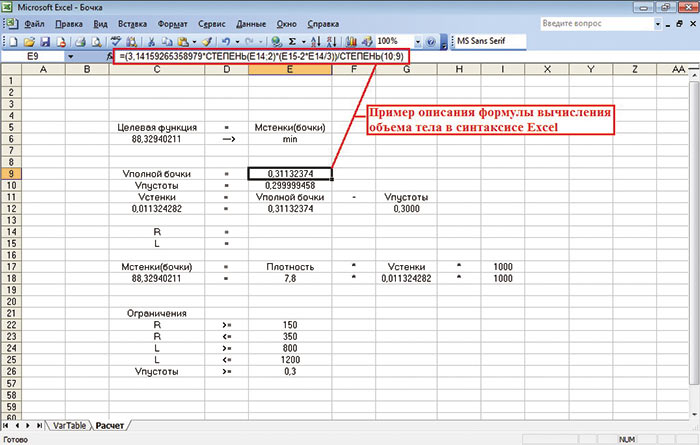
Рис. 10. Окно файла Excel с формулами, параметрами оптимизации и ограничениями

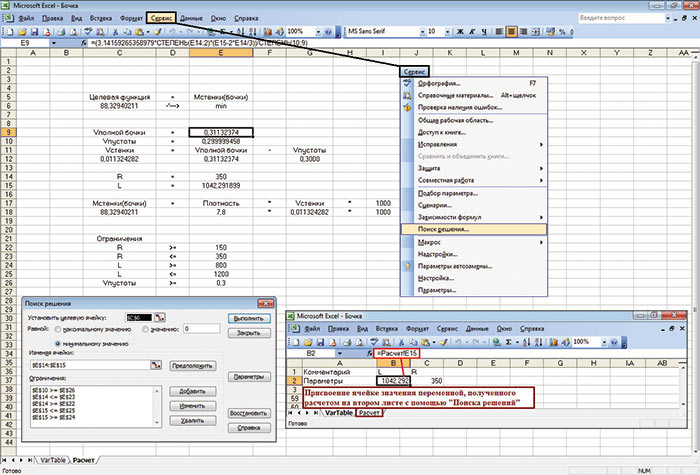
Рис. 11. Окно диалога Поиск решения и взаимосвязи ячеек файла Excel

К ограничениям относятся диапазон изменения R и L, а кроме того, учитывая толщину стенки бочки, — ее внутренний объем (пустоты) должен быть меньше 0,3 м3. Все параметры и условия заданы, остается вывести формулы расчета внутреннего объема бочки, а также формулу расчета объема самой бочки для определения целевой функции. Объем материала бочки (объем стенки), то есть тот объем, который занимает тонкостенная часть сосуда, будет вычисляться как разность объемов полнотелого сосуда (объем полной бочки без пустоты) и пустоты внутри сосуда. Не будем вдаваться в подробности выведения итоговых формул, а просто запишем их конечный результат.

Объем полнотелой бочки:

.

Объем пустоты внутри бочки:

  .

Эти формулы, а также формулы целевой функции, ограничения, параметры оптимизации необходимо записать на втором листе в окне созданного файла в синтаксисе Excel (рис. 10). Самое главное в файле Excel — это настроить все взаимосвязи нужных ячеек правильно. Некоторые ячейки носят сугубо информационный характер, то есть являются комментариями к вычисляемым ячейкам для удобства запоминания пользователем.

Далее настраиваем поиск решения через соответствующий диалог меню Сервис -> Поиск решения (рис. 11).

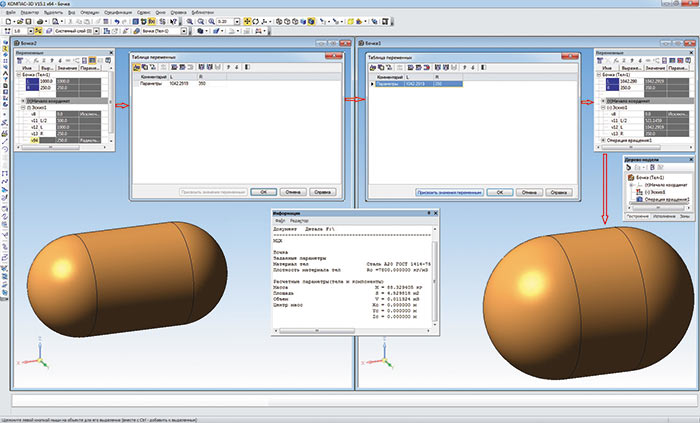
Рис. 12. Последовательность действий присвоения расчетных значений внешним переменным

Главная взаимосвязь настраивается как обычная связь одной ячейки с другой, только в данном случае необходимо с редактируемой ячейки первого листа осуществить взаимосвязь с одноименной ячейкой на втором листе, то есть создать ссылку.

Осталось сохранить файл и закрыть окно Excel. На этом работа в Excel заканчивается и возобновляется работа КОМПАС­3D. Открываем модель бочки с введенными ранее параметрами. В окне переменных заходим в диалог Таблица переменных и открываем файл Excel, в котором был произведен поиск оптимального решения. Чтобы внешние переменные присвоили значения данных, полученных оптимизацией, необходимо левой клавишей мыши выделить строку с нужными параметрами и нажать кнопку Присвоить значения переменным. В окне переменных значения переменных L и R преобразуются. После этого остается нажать клавишу «F5» и перестроить модель (рис. 12).

Для проверки своих расчетов можно вывести на экран информацию массово­центровочных характеристик и сравнить их с расчетом в файле Excel.

Таким нехитрым способом в КОМПАС­3D можно решать задачи оптимизации. 

С видеопримерами анимации и исходными файлами можно ознакомиться на странице в социальной сети «ВКонтакте» https://vk.com/sapr_animatsiya. 

САПР и графика 2`2015