Моделирование болтовых соединений в КЭ-комплексе SIMULIA Abaqus

Дмитрий Бузлаев
Руководитель Центра инженерного консалтинга ООО «ТЕСИС»

Болтовое соединение является широко распространенным дискретным соединением, применяемым в различных областях техники уже не одну сотню лет.

Тем не менее для инженера­прочниста моделирование болтового соединения и интерпретация полученных результатов является нетривиальной задачей, так как существуют различные подходы к моделированию в зависимости от цели расчета и диктуемых ею точности результатов, типа болтового соединения и приложенной к нему нагрузки, размерности и сложности рассматриваемой модели.

В задачах автомобилестроения болтовое соединение встречается не так часто, как соединение точечной сваркой или сварные и клеевые швы. Современные вычислительные комплексы позволяют производить детальный анализ болтовых соединений с использованием трехмерных объемных конечно­элементных моделей. Такой подход является наиболее очевидным и представляется достаточно простым, так как нет идеализации ножки болта одномерным элементом балки или коннектором, нет идеализации головки болта и гайки «пауком» из линейных элементов с эквивалентной жесткостью или же связями, кроме того, от таких моделей ожидается высокая точность результатов в сравнении с упрощенными моделями. Однако и в таком подходе существуют свои упрощения и свои подводные камни.

Первым упрощением является моделирование резьбы. В подавляющем большинстве случаев при практическом моделировании болтовых соединений объемными моделями резьба полностью не моделируется, поскольку иначе возрастает размерность задачи, требуется очень аккуратный подход к моделированию трения и затяжка должна быть промоделирована путем закручивания гайки, к которой приложен крутящий момент. Если не моделировать закручивание полностью, то теряется точность расчета, а вместе с ним и смысл моделирования резьбы. Чаще всего гайка «приклеивается» к ножке болта специальным типом связей (в Abaqus они носят название «tie»).

Другой подход заключается в задании контакта по гладким цилиндрическим поверхностями ножки и гайки, то есть гайка может скользить по ножке. При этом к свободному торцу гайки прикладывается давление, прижимающее ее к соединяемому фланцу, а к свободному торцу болта прикладывается эквивалентное растягивающее противодавление, имитирующее затяжку болта.

Затяжка болта — это второе упрощение при моделировании. Неучет затяжки может привести к раскрытию стыка между соединяемыми поверхностями, а это существенно изменит жесткостные характеристики модели. Одним из способов предварительной затяжки является описанный выше метод давления и противодавления. Другой способ представляет собой гибридное моделирование, особенно уместное при длинных болтах, работающих только на растяжение. При гибридном моделировании большая часть ножки заменяется элементом коннектора, не имеющим жесткости на сжатие, на котором для имитации затяжки задается перемещение одного узла относительно другого. Такой подход встречается всё реже, так как при сохранении точности расчета и сокращении вычислительных затрат он требует от прочниста дополнительных усилий по моделированию. Наиболее развитые конечно­элементные (КЭ) комплексы предлагают автоматизированное моделирование затяжки путем «схлопывания» одного из слоев элементов ножки. В Abaqus/Standard ножка делится плоскостью примерно посередине. К этой плоскости прикладывается так называемая болтовая нагрузка, задаваемая через силу или перемещение. Узлы слоя элементов, лежащие на этой поверхности, искусственно сближаются с противоположными узлами того же слоя, ножка укорачивается и за счет этого в ней создаются растягивающие нагрузки. Гайка, закрепленная на ножке связями «tie», и головка начинают давить на соединяемые детали, воспроизводя затянутый болт.

Третьей группой упрощений и допущений является моделирование контакта в болтовом соединении. Оно тесным образом связано с условиями применения болтов. Существует три различных режима работы болтовых соединений. Штифтовое соединение используется в основном в авиации, при этом ножка болта и отверстия под болт выполняются с одним диаметром с высокой точностью, затяжка болта в этом случае относительно мала. Такое соединение работает в основном на сдвиг, а следовательно, ножка болта работает на срез, а отверстия в деталях — на смятие. Очевидно, что при этом необходимо моделировать три контактные группы поверхностей: между внешними фланцами соединяемых деталей и головкой болта и гайкой; между внутренними фланцами соединяемых деталей; между ножкой болта и стенками отверстий соединяемых деталей. В случае трех соединяемых пластин, например, количество контактных пар для одного болта будет как минимум семь, плюс еще одна для моделирования неподвижного соединения гайки и болта. Шайбы, как правило, в расчете не учитываются. Нетрудно представить, что в случае необходимости моделирования, к примеру, 32 болтов количество контактных пар будет исчисляться сотнями. Это влечет за собой дополнительную работу по заданию таких пар, дополнительное время расчета, возможные проблемы со сходимостью решения и т.д. Тем не менее упрощение моделирования контакта в случае полного трехмерного моделирования соединения, работающего в штифтовом режиме, вряд ли возможно.

Вторым является режим продольного удержания, при котором отверстие под болт выполнено с зазором, детали работают на отрыв одна относительно другой, болт затянут таким образом, чтобы обеспечить нераскрытие соединения. В таком режиме можно пойти на определенные меры по сокращению числа контактных пар, сохранив при этом адекватное поведение модели. Можно отказаться от моделирования контакта между ножкой и стенками отверстий, можно вместо раскрывающегося контакта между головкой и фланцем и гайкой и фланцем связать их связями «tie», так как под растягивающей нагрузкой контакт между ними всегда будет сохраняться. Единственная контактная пара в этом случае — это контакт между фланцами соединяющихся деталей. В приведенном ранее примере, когда три пластины скреплены 32 болтами, контактных пар будет всего две. Однако болтовое соединение в этом режиме иногда может работать и на сжатие. В этом случае описанное нами упрощение недопустимо.

Наконец, третьим режимом работы является режим плотного соединения. При этом соединение подвержено комбинированной нагрузке — это и растяжение соединения, и сдвиг. Кроме того, нагрузка может изменяться по времени — растягивающая становится сжимающей и наоборот. Такая нагрузка характерна, например, для колесных болтов при качении колеса. Отверстие под болт, как и во втором случае, выполняется с зазором, болт затягивается нагрузкой большей, чем в первом случае, сдвиг одной детали относительно другой обеспечивается трением. При этом ножка болта зачастую нагружена изгибающей нагрузкой, контактное давление под головкой или гайкой неравномерно, поэтому необходимо моделировать их контакт с поверхностями соединяемых деталей. Из анализа можно исключить только контакт между ножкой и стенками отверстий. Отметим, что в режиме плотного соединения болт получает высокую растягивающую нагрузку уже в результате затяжки, далее к нему прикладывается эксплуатационная нагрузка, которая растягивает его еще больше. При этом соединение не должно раскрыться. Представим себе ситуацию, при которой соединение под максимальной нагрузкой все­таки раскрывается. При этом контактирующие поверхности соединяемых деталей разгружаются, но высокая нагрузка приходится на контакт с гайкой и головкой болта. Часто в таких соединениях болт выполнен из более прочного материала, чем соединяемые детали. При анализе таких соединений важным является достоверная картина распределения напряжений в соединяемых деталях — не исключено, что они начнут разрушаться раньше болта или гайки. Таким образом, анализ напряжений вообще и контактных давлений в частности является важнейшей задачей прочниста при моделировании болтовых соединений. При этом необходимо правильно моделировать контакт и интерпретировать результаты расчета в зоне контакта.

Рассмотрим некоторые важные моменты такого анализа в системе Abaqus/Standard. Несколько лет назад в Abaqus/Standard появилась функция General Contact, позволяющая значительно упростить задание контакта при работе над КЭ­моделью. В сущности, единственное, что для этого нужно сделать, — включить General Contact, и он начнет работать для всех внешних поверхностей всех деталей в вашей сборке. В свойствах контакта можно ничего не задавать, набор параметров по умолчанию в большинстве случаев позволяет получить адекватный результат и хорошую сходимость решения. В алгоритме контактного анализа важны следующие составляющие: метод дискретизации контактных поверхностей, учет относительного скольжения, метод наложения контактных условий и зависимость контактного давления от взаимопроникновения. General Contact по умолчанию использует дискретизацию контакта «поверхность — поверхность», конечное (немалое) скольжение, метод штрафных функций и «жесткий» контакт (бесконечный рост давления при взаимопроникновении поверхностей). General Contact внутри алгоритма автоматически назначает роли управляющей и управляемой поверхностям (master­slave), алгоритм обеспечивает идентичные результаты при смене ролей. General Contact значительно ускоряет процесс задания контакта, однако при существенной экономии времени пользователя на задание контактных пар значительно снижается скорость расчета (так как в поиске контакта перебираются все поверхности деталей в сборке). Разработчики говорят примерно о 25­40­процентном замедлении скорости расчета. Тем не менее при использовании General Contact, как правило, улучшается сходимость решения, поэтому при меньшем количестве инкрементов и итераций решения за один шаг расчета потери времени на вычисления не слишком заметны. В General Contact можно выделять отдельные поверхности, которые будут активны в контакте, а остальные будут игнорироваться. Это может значительно поднять скорость расчета и в определенных случаях повысить точность некоторых результатов.

Кроме того, в Abaqus по­прежнему поддерживается моделирование контакта с помощью контактных пар. Контактные пары могут быть заданы совместно с функцией General Contact. При использовании препроцессора Abaqus/CAE существует возможность автоматического поиска контактных пар, что значительно упрощает их задание. Контактные пары также могут быть настроены на использование алгоритмов, аналогичных алгоритмам в General Contact, но пользователь должен хорошо разбираться в контактном анализе и применяемых настройках. Abaqus/CAE облегчает задание рекомендованных настроек, но нужно иметь в виду, что для контактных пар они не являются настройками по умолчанию. Об этом стоит помнить инженерам, использующим сторонние препроцессоры для работы с Abaqus/Standard — в них по умолчанию могут быть иные настройки. Чтобы подвести черту под применением настроек и перейти к конкретным примерам, мы рекомендуем использовать General Contact и не менять настройки по умолчанию, если у пользователя нет четкого представления о том, для чего они нужны.

При работе с реальными деталями сложной формы довольно часто приходится применять автоматическую генерацию сетки элементами тетраэдров. Уже давно общей практикой стало использование элементов тетраэдров второго порядка, то есть с промежуточными узлами на ребрах. Вплоть до середины 2000­х годов в случае применения этих элементов в контактном анализе в большинстве конечно­элементных комплексов довольно часто возникали серьезные проблемы с вычислением контактных давлений. Контактные давления рассчитываются на основании сил в узлах, находящихся в контакте, а они в классических тетраэдральных элементах второго порядка могут иметь противоположный давлению знак, что вызвано функциями формы таких элементов (глубоко в теорию мы здесь погружаться не будем). Особенно болезненной эта проблема была при дискретизации контакта по типу «узел — поверхность». Более современная дискретизация по типу «поверхность — поверхность» дает более реалистичную, гладкую картину распределения контактных напряжений, менее зависящую от типа элементов, используемых в расчете, и соответствия размеров элементов одной и другой контактной поверхности. Алгоритм «поверхность — поверхность», применяемый в General Contact, обеспечивает эффективное использование тетраэдров второго порядка в сетках контактирующих деталей. В Abaqus/Standard наиболее часто применяется тетраэдр второго порядка C3D10. Кроме того, существуют новый элемент C3D10I, позволяющий получить точную (без интерполяции) визуализацию напряжений по поверхностям, и более старый C3D10M, созданный, в частности, для использования в контактных задачах с применением алгоритма «узел — поверхность». В настоящее время в General Contact имеет смысл использовать C3D10M только в случае, если вы планируете применять метод множителей Лагранжа вместо метода штрафных функций. В дальнейшем в этой статье, когда речь зайдет о тетраэдрах, будет предполагаться использование только элемента C3D10.

Рассмотрим классический пример с отверстием в прямоугольной панели конечных размеров под растягивающей или сжимающей нагрузкой (Тимошенко С.П., Гудьер Дж. Теория упругости. М.: Наука, 1975). Известно, что присутствие такого отверстия приводит к концентрации напряжений на внутренней кромке отверстия в самом узком сечении пластины. Изменим постановку задачи таким образом, чтобы отслеживать пиковое значение напряжений как контактное давление (рис. 1).

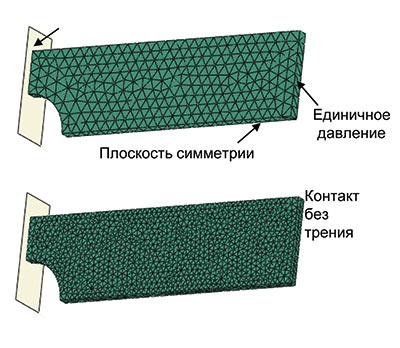
Рис. 1

Рассмотрим четверть пластины, зададим условие симметрии по горизонтальной плоскости и контакт без трения с абсолютно твердой стенкой, заменяющей вертикальную плоскость симметрии. К свободному торцу приложим единичное давление. Аналитическое решение дает значение 4,3 для точки А с концентрацией напряжений. Проведем расчеты с грубой и с густой сетками элементов C3D10. На рис. 2 видно, что при сгущении сетки значение контактного давления меняется с 4,03 до 4,16.

Характерным поведением напряжений в зоне концентратора является приближение к некоторому постоянному значению при сгущении сетки. На рис. 3 показан индикатор ошибки контактного давления.

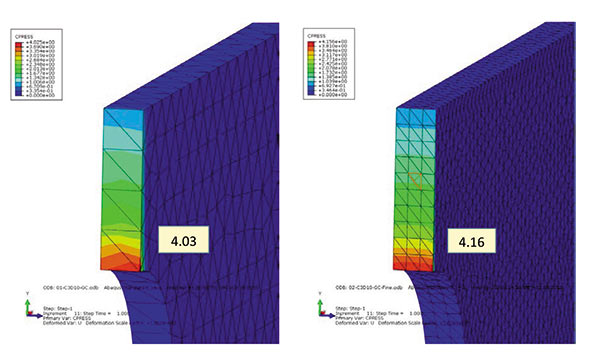
Рис. 2

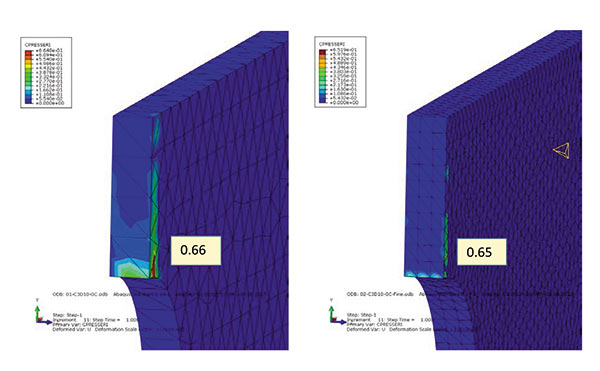
Рис. 3

Он имеет ту же размерность, что и давление, и показывает на места, в которых происходит резкое изменение контактного давления. Как уже говорилось, величина контактного давления в Abaqus рассчитывается на основании узловых сил в зоне контакта и площади активного контакта. При этом происходит определенная фильтрация пиков рассчитанного давления, которая особенно высока в областях, смежных с зонами активного контакта. Это хорошо видно на боковых стенках панели, которые в активном контакте не участвуют, но по умолчанию в General Contact являются контактными поверхностями, так как описывают внешнюю поверхность тела. Индикатор ошибки CPRESSERRI имеет в данном примере максимальные значения (0,66­0,65) именно на боковых стенках. Это составляет 16,5 и 15,7% от пиковых давлений. Можно попробовать поднять точность отображения контактного давления, включив в алгоритм поиска контакта General Contact только активные поверхности, то есть жесткую стенку и торец пластины. При этом получаем значения давления 4,17 и 4,298 (рис. 4).

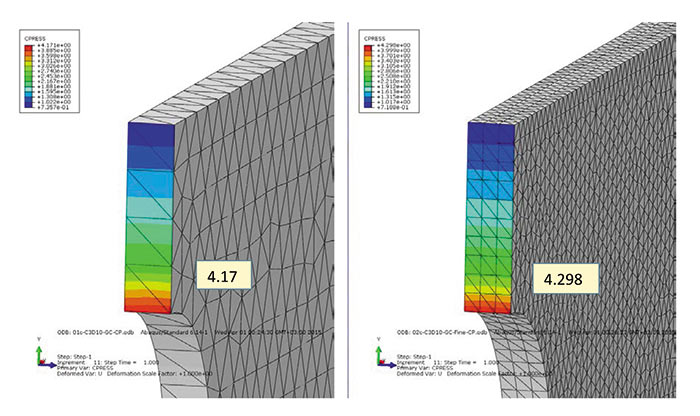
Рис. 4

Рис. 5

Индикатор ошибки показывает 6,3 и 0,15% от пиковых давлений соответственно. Видно, что в случае густой сетки значение контактного давления максимально приближается к теоретическому, и достигнуто это было лишь выделением активных поверхностей в General Contact. Такое выделение, в принципе, не сильно отличается по трудоемкости от обычного задания контактных пар, его следует применять лишь в отдельных редких случаях для проверки точности решения для напряжений и для ускорения скорости расчета. Посмотрим, как данный прием отразится на величине контактного давления при использовании гексаэдральных элементов первого порядка C3D8R, которые также очень часто применяются при моделировании в Abaqus. На рис. 5 показано различие между результатами при использовании всех поверхностей по умолчанию и только активных контактных поверхностей, заданных в General Contact через Contact Pairs.

В первом случае мы видим 3,5, во втором — 3,94. Сетка соответствует грубой сетке из элементов C3D10. Из этого примера виден, во­первых, сглаживающий эффект линейных элементов с редуцированной схемой интегрирования, во­вторых, отсутствие влияния боковых поверхностей на результаты, характерное для элементов второго порядка. На рис. 6 показан результат для контактного давления для густой сетки элементов C3D8R — 4,15. Прослеживается та же тенденция приближения к аналитическому решению, но здесь сходимость гораздо медленнее, чем для элементов тетраэдров второго порядка.

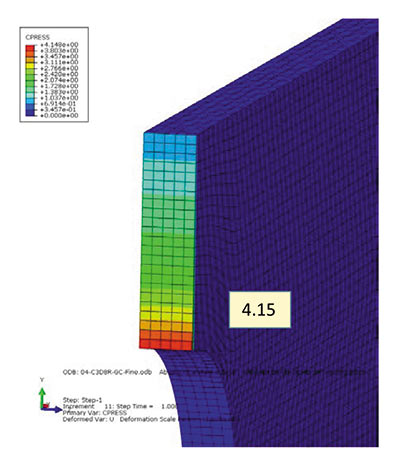
Рис. 6

Задачи с сингулярностью контактных напряжений отличаются по поведению от задач с концентраторами прежде всего тем, что при сгущении сетки, особенно элементов второго порядка, напряжения резко возрастают и какого­то насыщения, приближения к определенному значению не происходит. Эквивалентные напряжения при этом могут многократно превышать предел текучести для заданного материала, если его свойства описаны в модели только в упругой зоне. Основными причинами сингулярности являются упрощения в модели, которые приводят к усложнению жизни прочниста. Простейший пример сингулярности — напряжения в области сосредоточенной нагрузки. Чтобы вычислить напряжение, необходимо разделить определенное значение силы на площадь, к которой она приложена. В случае сосредоточенной нагрузки площадь равна нулю. Далее читатель может легко представить, что получится, если рассчитывать напряжение, деля ненулевую силу на ноль. Сингулярность в контакте твердого тела с упругим или упругого с упругим также возникает по причине резкого изменения условий контакта на кромке контактирующего тела: в зоне контакта присутствует ненулевое давление, а сразу же за кромкой его нет, оно равно нулю. Переходного участка нет, и это вызывает сингулярность контактного давления на кромке. Сингулярность не является естественным явлением, поскольку в детали не может быть бесконечных напряжений. В общем случае можно свести причины сингулярности поля напряжений к трем упрощениям, вызванным применением линейной теорией упругости, — линейной зависимости между напряжениями и деформациями (упругий отклик), линейной зависимости деформаций от градиентов перемещений (малые деформации) и приложению нагрузки к недеформированной системе на протяжении всего процесса приложения (малость перемещений). Сингулярность является нарушением всех трех допущений, при этом, как ни странно, вытекает из формул, их описывающих.

Рассмотрим простой пример контакта большого и маленького упругих кубиков. Большой кубик закреплен по нижней грани, к верхней грани маленького кубика приложено единичное распределенное давление. В задаче используются все описанные выше допущения. Можно было бы ожидать равномерного единичного контактного давления на нижней поверхности кубика, однако этого не происходит из­за сингулярности на кромке, а особенно — в вершинах кубика. На рис. 7 показано, как растет контактное давление в вершине маленького кубика по мере сгущения сетки.

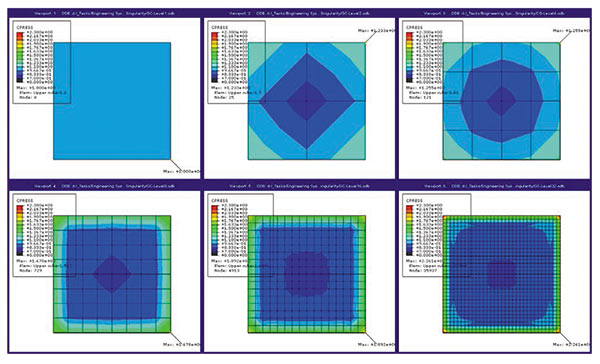
Рис. 7

Значение давления меняется от 1 до 2,26 при самой густой сетке, где размер элемента равен 1/32 размера грани кубика. В качестве элемента используется гексаэдр первого порядка C3D8R. Интересно сравнить, как «чувствует» сингулярность элемент второго порядка C3D10. Для сетки из C3D8R с длиной стороны 1/16 мы имеем значение напряжений в вершинах в 1,89, а для сетки из элементов C3D10 c длиной стороны 1/8 — 2,25. Практического значения этот результат не имеет, но качественно показывает более высокую чувствительность элементов второго порядка не только к концентраторам, но и к сингулярностям. Интересно отметить, что для линейных элементов эффект сингулярности затухает через два ряда элементов, в то время как в элементах второго порядка затухание происходит быстрее — уже во втором ряду.

Рассмотрим пример с колесным диском. В нашей практике нам часто приходится иметь дело с аналогичными задачами наших заказчиков, но конкретно этот пример нереальный — он взят из курса Abaqus по контактному анализу (рис. 8).

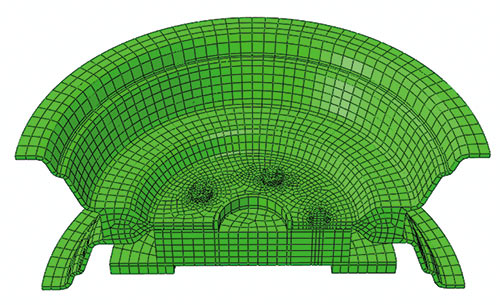
Рис. 8

Диск выполнен из штампуемого сплава алюминия с пределом текучести 110 MПa, материал задан как упругий (в реальной практике алюминиевые диски делают из другого, более прочного сплава). Шпильки и гайки, а также ступица выполнены из стали (упругий материал). Все детали в сборке разбиты гексаэдрами C3D8R, гайки — тетраэдрами C3D10. В качестве случая нагружения рассматривалась только затяжка гаек.

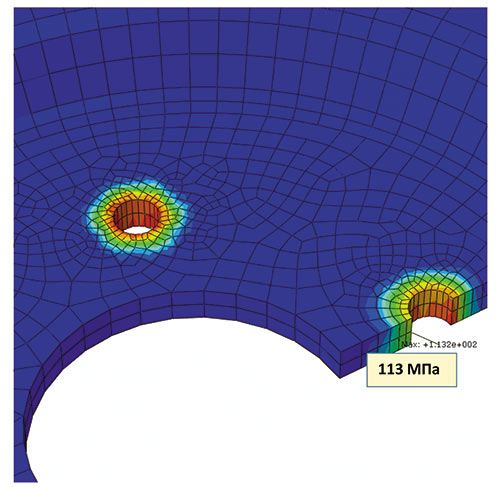
Рис. 9

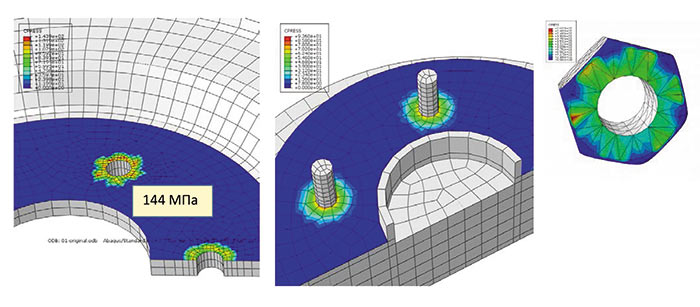
Рис. 10

На рис. 9 показаны эквивалентные напряжения в диске — они равны 113 МПа, что очень близко к пределу текучести материала диска.

На рис. 10 показаны контактные давления по активным поверхностям (в исходной модели использовались четыре контактные пары, коэффициент трения в контакте — 0,1).

Давление в 144 МПа на интерфейсе «гайка — диск» неравномерное из­за относительно грубой сетки даже для дискретизации «поверхность — поверхность». Если же необходимо достаточно точно определить контактные давления либо максимальные главные напряжения (например, для последующего анализа усталостной прочности диска), необходимо сгустить сетку диска. В общем случае соединяемые детали могут иметь сложную форму, которую неэффективно или невозможно разбить на гексаэдры, поэтому для того, чтобы сделать наш пример более общим, перейдем на сетку тетраэдров второго порядка и посмотрим, как изменятся распределение давлений и эквивалентные напряжения. Кроме того, вместо контактных пар используем General Contact. На рис. 11 видно неравномерное распределение контактного давления на диске со стороны ступицы.

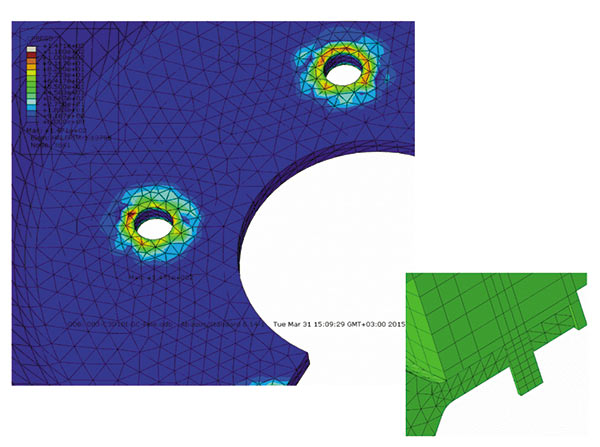
Рис. 11

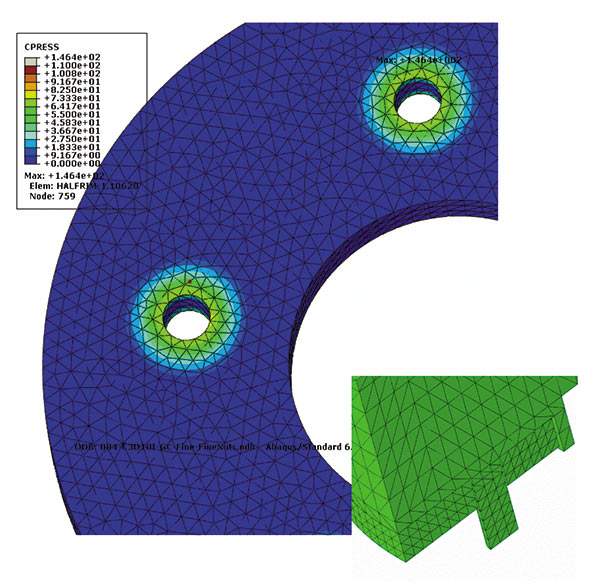
Рис. 12

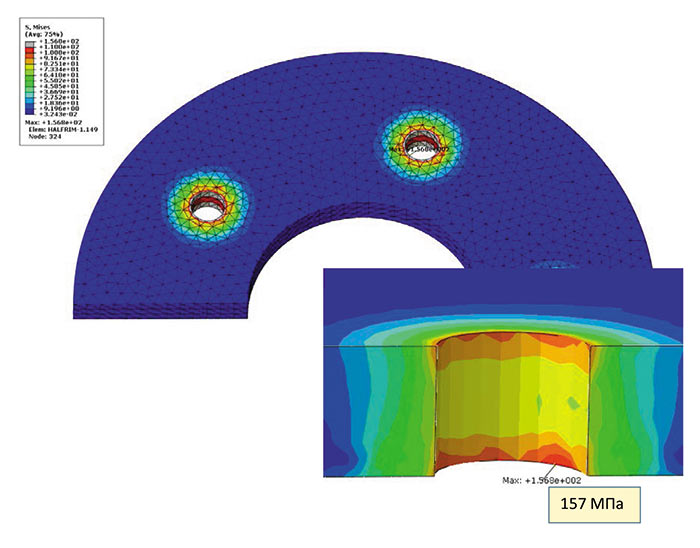
Рис. 13

Пики могут быть вызваны слишком большим различием между характерными размерами элементов диска и элементов ступицы: расстояние между узлами в диске 3 мм, а в ступице — 6­10 мм. Зададим ступицу тетраэдрами с аналогичным размером элемента. Теперь контактное давление более равномерно (рис. 12), но если обратить внимание на эквивалентные напряжения в диске, то видно (рис. 13), что они выросли до 157 МПа на кромке отверстия и превысили предел текучести при переходе на новую сетку.

Велика вероятность, что мы имеем дело с сингулярностью. Что делать в этом случае? Как интерпретировать результаты?

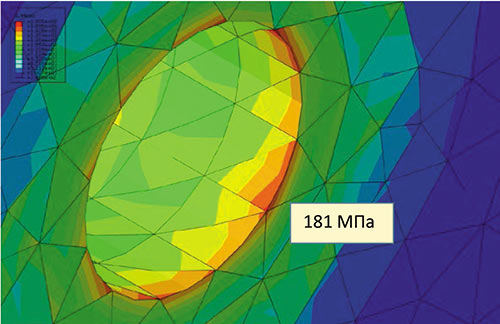
Рис. 14

В самом простом случае прочнист, убедившись в наличии сингулярности, может игнорировать эти пики напряжений и использовать значения на расстоянии примерно одного элемента от кромки (для элементов второго порядка). Однако это неприменимо, если поле напряжений должно использоваться в последующих расчетах, например при оценке долговечности детали. Следует помнить, что величина напряжений, показываемая заливкой, получена в результате дополнительной обработки. По умолчанию при отрисовке напряжений мы имеем дело со значениями, во­первых, сглаженными, а во­вторых, экстраполированными из точек интегрирования на поверхность элемента. Если отменить сглаживание, то мы получим максимум в районе 181 МПа (рис. 14), но и это значение окажется не совсем точным, так как было подвергнуто экстраполяции.

Собственно говоря, сглаживание по поверхности является осреднением экстраполированных значений с учетом значений в соседних элементах. Значение напряжения, не подвергнутое никакой дополнительной обработке, можно взять непосредственно из точки интегрирования с помощью «пробника» в Abaqus/CAE (рис. 15).

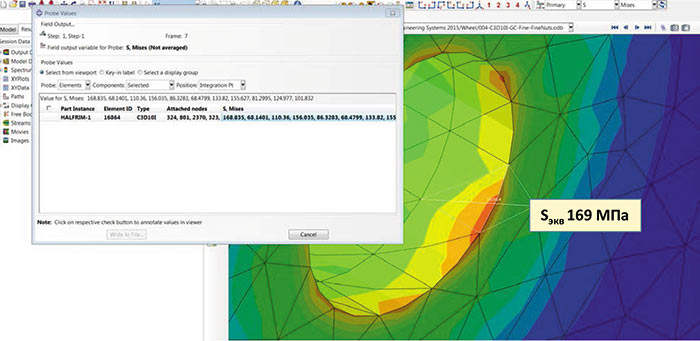
Рис. 15

Оно будет равно 169 МПа, что близко к усредненному значению и принципиально не меняет картину напряженного состояния. В дальнейшем для простоты мы будем использовать именно осредненное значение на поверхности элемента. Как уже упоминалось, одной из причин появления сингулярности при контакте является резкое падение контактного давления на кромке. Это характерно для случаев, когда грань в контакте и боковая грань имеют значительный угол между нормалями. Можно попытаться устранить эту проблему путем введения галтели вместо острой кромки. В реальности на любой острой кромке всегда присутствует тот или иной радиус (иногда невидимый глазу). Тем не менее его моделирование может привести к очень густой сетке с размером элемента, на порядки отличающимся от среднего размера по модели, а это не совсем практично. Может помочь субмоделирование, предусмотренное в Abaqus, когда расчет проводится сначала на глобальной модели, а затем на субмодели, описывающей малый изолированный участок детали, к которому прикладываются граничные условия, полученные из анализа глобальной модели. В данной работе в качестве компромиссного варианта мы попробовали ввести фаску размером в 1 мм на одном из отверстий (рис. 16).

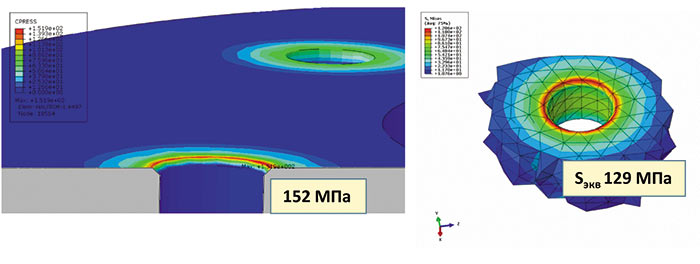
Рис. 16

Такая фаска приводит к росту контактного давления из­за уменьшения поверхности контакта и одновременному снижению эквивалентных напряжений до 129 МПа.

Наиболее эффективным методом, с нашей точки зрения, является применение упруго­пластической модели материала диска. Мы рекомендуем использовать реальную кривую упрочнения материала, тем более что эта информация достаточно доступна. Более простым путем будет задание пластического участка в виде линейной функции. Для этого необходимо задать начальные и конечные точки, при этом ввести определенный наклон прямой на пластическом участке, чтобы промоделировать упрочнение. Наконец, весьма распространено использование идеально пластического материала без упрочнения. Однако при этом по достижении предела текучести материал полностью теряет свою несущую способность, что может привести к проблемам со сходимостью решения. Напомним, что вводится исключительно пластический участок в координатах «логарифмические пластические деформации — истинные напряжения». После затяжки болтового соединения напряжения по Мизесу сразу снижаются до 110 МПа — предела текучести (рис. 17).

Что интересно: пластические деформации в районе отверстия с фаской равны нулю и только в области отверстия, на котором мы оставили острую кромку, достигли примерно 0,001 (рис. 18). Следовательно, мы добились своей цели — убрали сингулярность, но при этом материал «не уходит в пластику».

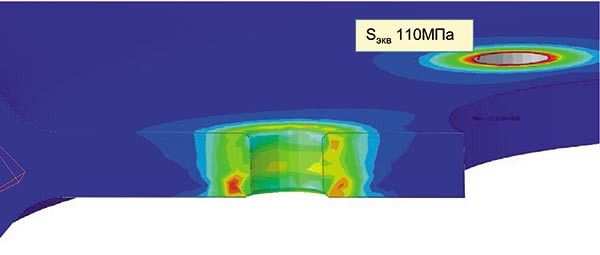
Рис. 17

Напомним, что в достаточно грубой начальной модели мы также имели аналогичный уровень напряжений.

Из всего вышеизложенного можно сделать следующие выводы: General Contact в Abaqus позволяет эффективно моделировать контакт, в том числе и при работе с болтовыми соединениями. Он поддерживает возможность работы с элементами как первого, так и второго порядка. В Abaqus/Standard для таких задач чаще всего используются C3D8R и C3D10(I). Применение C3D10 дает уточненные результаты для распределения напряжений. Однако при этом пиковые значения могут расти при сгущении сетки, что указывает на сингулярность, характерную для кромок тел в контакте. Проведение адекватного анализа результатов потребует уточненного моделирования геометрии (фаски, галтели) для сглаженного перехода от свободной поверхности к активной контактной поверхности. Кроме того, потребуется уточненное моделирование материала с помощью упруго­пластической модели с заданием кривой упрочнения. В отдельных случаях имеет смысл аккуратно моделировать контакт упругих тел с жесткими поверхностями путем задания отдельных активных поверхностей в контакте, а не всего экстерьера.

Компания ТЕСИС предлагает различные виды учебных курсов по использованию КЭ­комплекса Abaqus, в том числе и посвященных моделированию контакта в системе Abaqus и различных дискретных соединений. 

САПР и графика 5`2015