Методика моделирования течения металлического теплоносителя в первом контуре ядерного реактора
Предлагается методика моделирования работы первого контура ядерного реактора с металлическим теплоносителем. Ключевая идея методики заключается в декомпозиции большой и сложной задачи на отдельные независимые подзадачи и их дальнейшей связи через согласованные граничные условия. Описывается функционал FlowVision, позволяющий упростить расчеты, не теряя точности получаемого решения. Рассказывается о применении модификаторов — элементов, изменяющих решение и расчетную область. Идеи данной методики могут быть использованы для решения любых сложных и трудоемких задач.
Ядерный реактор — это устройство для осуществления управляемой цепной ядерной реакции. Основным его назначением является получение энергии, необходимой для общества. Схема корпусного реактора представлена на рис. 1.
Корпус реактора состоит из цилиндрического сосуда и крышки, соединяемой с корпусом шпильками. Изнутри корпус реактора нагружен давлением теплоносителя. Теплоноситель с помощью главного циркуляционного насоса (ГЦН) поступает в напорную камеру, где через перфорированные конструкции, выравнивающие поток, и через нижнюю опорную решетку попадает в активную зону.
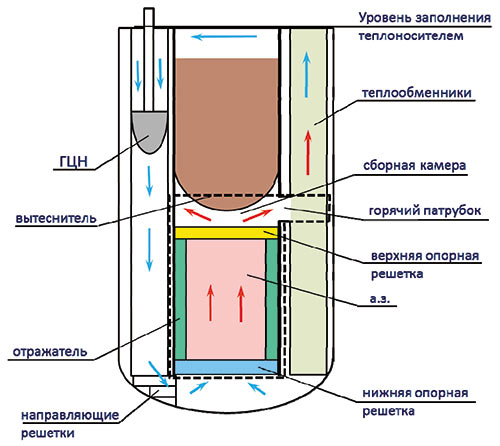
Рис. 1. Схема ядерного корпусного реактора
с металлическим теплоносителем
Активная зона (далее — АЗ) является центральной частью реактора, в ней находится ядерное топливо, выделяющее энергию, а также органы системы управления и защиты (СУЗ). Вокруг АЗ для уменьшения утечки нейтронов располагается отражатель.
Теплоноситель, поступивший через перфорированную нижнюю опорную решетку, движется вверх, нагревается, проходя через АЗ, и через верхнюю опорную решетку попадает в сборную камеру, откуда направляется в теплообменники, отдавая теплоту во второй контур с водяным теплоносителем. Далее охлажденный теплоноситель снова попадает в напорную камеру реактора, и основной циркуляционный контур замыкается.
Математическое моделирование процессов, проходящих в реакторе, с подробным разрешением расчетной сеткой всех геометрических особенностей — задача ресурсоемкая и трудоемкая, она требует больших вычислительных мощностей и значительных затрат времени. Для эффективного решения сложных задач рекомендуется их декомпозировать на несколько независимых подзадач с собственной постановкой, которые между собой будут связаны через согласованные граничные условия.
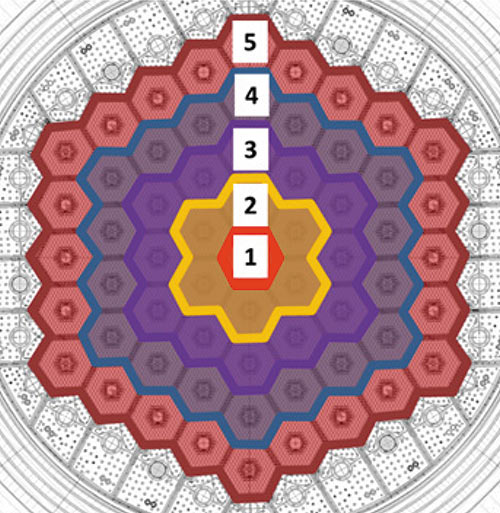
Рис. 2. Разбивка АЗ реактора
на кольца для установки модификаторов объемного источника тепла
Например, отдельный расчет режимов работы ГЦН позволит получить значения расходов и давлений в напорной камере, а также определить силы, действующие на лопасти насоса. Это дает возможность проводить прочностные расчеты в стороннем расчетном коде с последующим определением усталостных характеристик рабочего колеса насоса.
Аналогичным образом возможно определить характеристики процессов, происходящих в АЗ, так как сама конструкция реактора позволяет разделить проточную часть первого контура реактора на несколько отдельных расчетных подобластей и рассмотреть течение теплоносителя в рамках независимой постановки задачи для каждого участка с предварительным определением тепловыделения и гидравлического сопротивления в конструктивных элементах реактора. Используя данные, полученные в результате решения таких подзадач, опытный пользователь может собрать свою большую задачу, избежав при этом излишней детализации ее постановки.
Перед авторами данной статьи стояла задача определения температурной и скоростной неравномерности в сборной камере реактора, а также среднерасходной температуры в «горячем» патрубке на основании данных, полученных в точках установки термопар. При этом требовалось оптимизировать постановку задачи с целью уменьшения размерности расчетной сетки при сохранении требуемой точности решения. Как известно, объем сетки обусловлен особенностями задачи — как геометрическими (малоразмерные детали конструкции реактора, но влияющие на течение), так и физическими особенностями течения. Помимо этого размер расчетной сетки зависит от конфигурации самой расчетной области — секторная постановка, симметричная постановка или полная геометрическая постановка.
На выбор конфигурации расчетной области повлияли исходные данные: тепловыделение в АЗ, полученное из кода нейтронного переноса; гидравлическое сопротивление решетки АЗ, рассчитанное на основе конфигурации конструкции АЗ (см. рис. 1, расчетная область выделена прерывистой линией). Были известны расход и начальная температура теплоносителя, тепловыделение в АЗ, а также перепад статического давления в ряде элементов реактора. Температурные и скоростные поля на входе в нижнюю опорную решетку были приняты равномерными, поскольку поток теплоносителя подходит туда через специальные направляющие, выравнивающие поток конструкции.
Применение специального функционала FlowVision (модификаторов — элементов, позволяющих изменять решение и расчетную область) позволило неявным (с точки зрения геометрии) образом через уравнения учесть геометрические особенности задачи, исключив из геометрической постановки малоразмерные детали геометрии АЗ.
Для моделирования тепловыделения в АЗ был применен модификатор объемного источника тепла, задающий тепловыделение в объекте, на котором он создан. Поскольку в АЗ наблюдается неравномерное выделение тепла как по радиусу, так и по высоте, вся АЗ была разделена на кольцевые зоны (рис. 2). Внутри каждого такого кольца изменение тепловыделений по высоте описывалось функциональными зависимостями.
Чтобы избавиться от малоразмерных деталей геометрии в элементах с пористой периодической структурой (АЗ, теплообменники, решетки) применялся модификатор гидравлического сопротивления, задающий изотропное сопротивление. С помощью заданного сопротивления вычисляется сила изотропного сопротивления, входящая в состав уравнений Навье — Стокса [1].
Таким образом, для элементов, перепад давления на которых изначально известен, был рассчитан коэффициент гидравлического сопротивления по формуле:
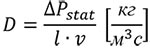
где:
ΔPstat — перепад статического давления [Па];
l — длина участка, на котором определяется перепад давления [м];
v — скорость течения теплоносителя [м/с].
Для пористых или периодических элементов, на которых неизвестен перепад статического давления, решались отдельные подзадачи с целью определения удельных гидравлических характеристик.
Рассмотрим это на примере расчета гидравлических сопротивлений в зазоре между корпусом и отражателем. Внешний вид отражателя приведен на рис. 3. Снаружи отражатель имеет обечайку, состоящую из множества пластин. Данные пластины были условно поделены на одинаковые повторяющиеся группы, и коэффициент гидравлического сопротивления рассчитывался внутри одной такой группы. На рис. 3 на обечайке отражателя выделен один периодический элемент, рядом показаны два варианта выбранных расчетных моделей, включающих один и три периодических элемента обечайки.
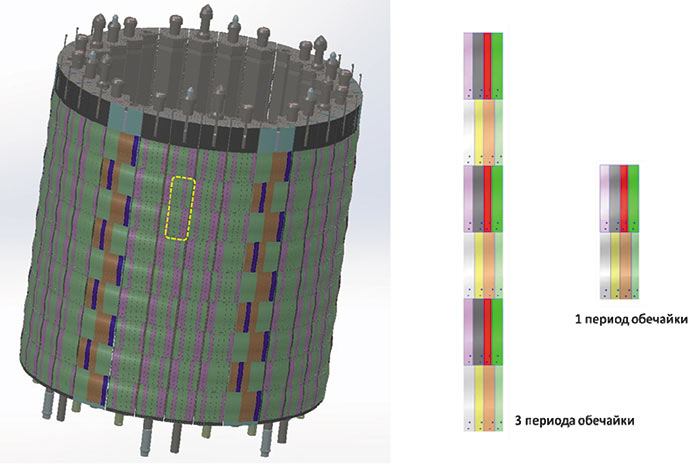
Рис. 3. Внешний вид отражателя (а) и варианты расчетных областей для определения коэффициента гидравлических сопротивлений (б)
В варианте, включающем три повторяющихся элемента обечайки, перепад давления оценивался по среднему элементу. Такая постановка позволила исключить влияние граничных условий, установленных на входном и выходном участках расчетной области. Вариант с одним повторяющимся, или периодическим, элементом обечайки давал существенное снижение размерности задачи (объем расчетной сетки), а следовательно, минимизировал время ее решения.
В ходе решения данной подзадачи учитывались следующие допущения:
- поскольку диаметр отражателя гораздо больше размеров периодического элемента обечайки, рассматривалась прямая обечайка, без учета радиального изгиба;
- в расчете не учитывалась упругость элементов обечайки. Они приняты абсолютно жесткими и установленными вплотную к стенкам отражателя;
- не рассматривается влияние крепежных элементов.
После прогонки первых задач и сравнения результатов было определено, что разница в перепаде давления в первой и второй постановке составила менее 2%. Поэтому для расчетов была выбрана модель, содержащая один периодический элемент обечайки. Расчеты проводились для различного значения температуры и скорости течения теплоносителя. Расстановка граничных условий (ГУ) и фрагмент расчетной сетки показаны на рис. 4.
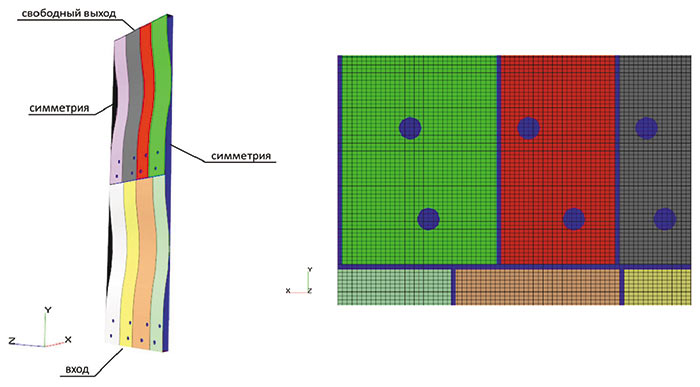
Рис. 4. Расстановка ГУ в расчетной области: а — все неуказанные ГУ — расчетная сетка; б — фрагмент расчетной сетки
В результате проведенных расчетов были определены величины перепадов статического давления, по которым найдены коэффициенты гидравлического сопротивления для разной величины температуры и скорости течения теплоносителя. На основании полученных значений были разработаны описывающие их математические функциональные зависимости. Таким образом, была решена подзадача, результаты которой позволили упростить расчет течения в первом контуре ядерного реактора.
Перейдем к постановке задачи моделирования работы реактора. Поскольку модель реактора симметрична, рассматривалась ¼ часть его геометрической модели. На рис. 5 представлена основная расчетная область и элементы конструкции, помещенные в нее с помощью модификатора подвижного тела (сами тела в расчете неподвижны).
Верхняя опорная решетка моделируется в явном геометрическом представлении, поскольку следующим этапом решения задачи являлась оптимизация конструкции данной решетки для улучшения перемешивания теплоносителя.
Во всей расчетной области учитывался гидростатический слой, создающий распределение давления по высоте АЗ. В качестве начальных условий установлено распределение значения температуры теплоносителя и его скорости в цилиндрической части реактора в соответствии с рассматриваемым расчетным случаем. Задание начальной скорости помогает сократить время получения сошедшегося решения. Данная скорость должна быть близкой по значению к ожидаемой скорости. Задание слишком большой скорости приводит к увеличению времени выхода задачи на установившийся режим.
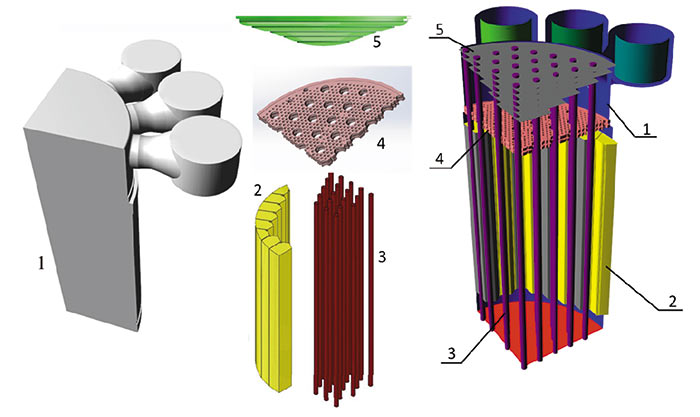
Рис. 5. Геометрическая модель расчетной области: 1 — корпус реактора (расчетная область), 2 — отражатель, 3 — каналы органов СУЗ,
4 — верхняя опорная решетка; 5 — вытеснитель
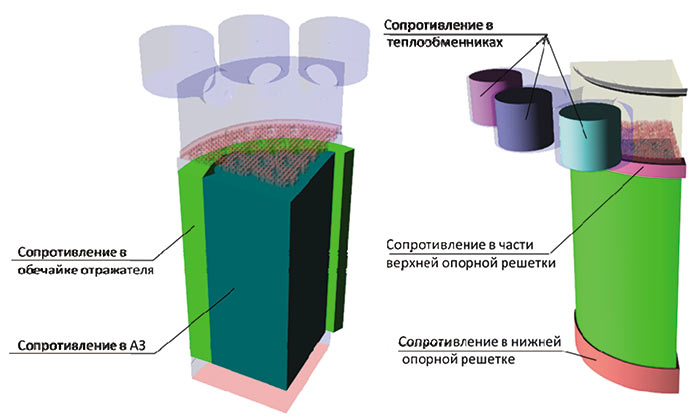
Рис. 6. Расстановка модификаторов сопротивления в расчетной области
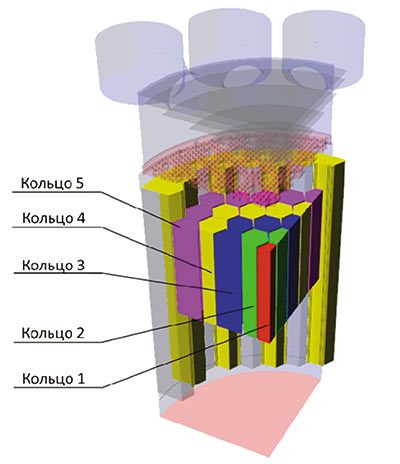
Рис. 7. Расстановка модификаторов объемного источника тепла в расчетной области
Рис. 6 иллюстрирует положение пористых тел в расчетной области, в каждом из которых установлен модификатор сопротивления.
На рис. 7 показана расстановка модификатором объемных тепловыделений.
В задаче рассчитывались уравнения движения ньютоновской жидкости, описываемые уравнениями Навье — Стокса, уравнения теплопереноса, моделирующие конвекцию и теплопроводность и уравнения турбулентности для стандартной keмодели. Выбор модели турбулентности в данном случае был обусловлен значениями величины y+.
Расстановка граничных условий представлена на рис. 8. На ГУ «вход» установлены нормальная массовая скорость и температура в соответствии с расчетным случаем, на ГУ «свободный выход» задано нулевое статическое давление.
Для нахождения оптимальной по размерам расчетной сетки и оценки точности получаемого решения было проведено исследование сходимости по сетке. Проводилась серия расчетов одной и той же задачи на сетке, которая последовательно сгущалась в области расчета. Сходимость оценивалась по следующим параметрам:
средняя температура в верхней сборной камере МБР;
силы, действующие на корпус реактора, и расход на одном из ГУ «свободный выход».
На рис. 9 приведены некоторые результаты, полученные для различных сеток, — от самой грубой (сетка 1) до самой подробной (сетка 4).
На основании представленных графиков для расчета была выбрана сетка 3, позволяющая получить требуемую точность решения с минимально возможным объемом сетки. Внешний вид выбранной сетки показан на рис. 10. Она состояла из равномерной начальной сетки и ряда объемных адаптаций. Итоговая размерность сетки составила около 8 млн ячеек.
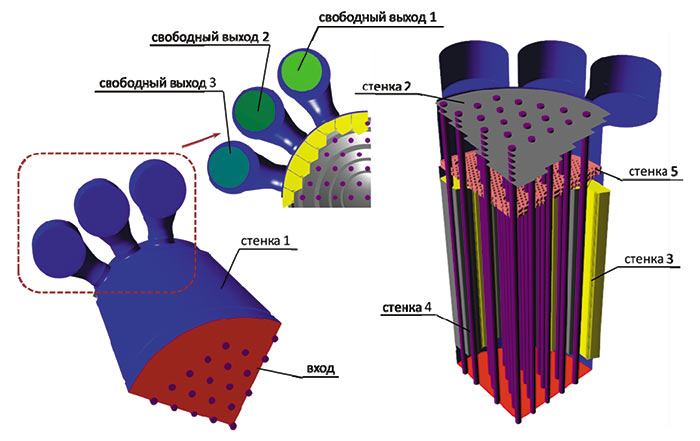
Рис. 8. Расстановка граничных условий в расчетной области
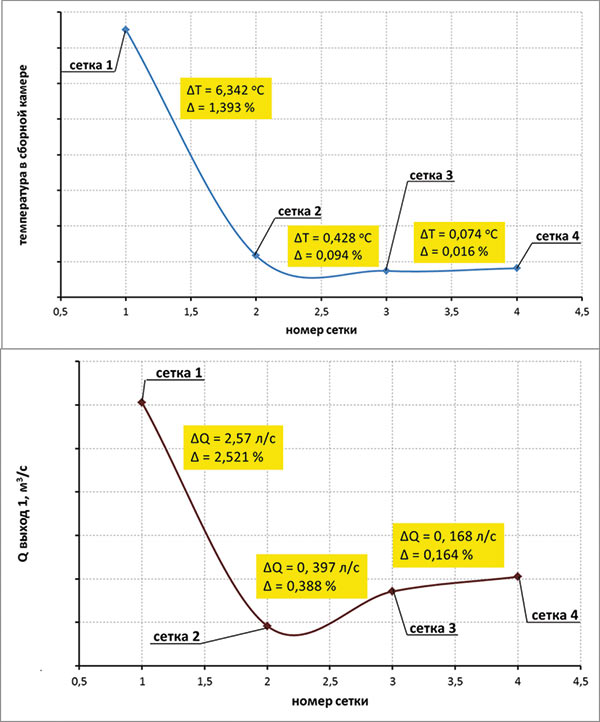
Рис. 9. Графики сходимости решения на различных расчетных сетках
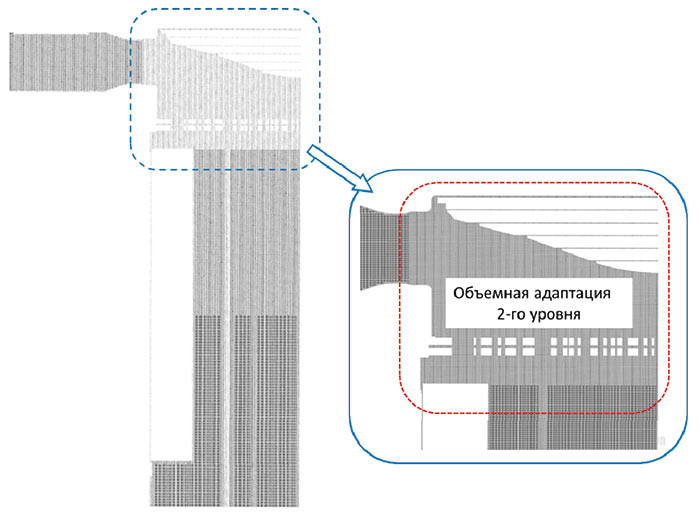
Рис. 10. Сечение выбранной расчетной сетки
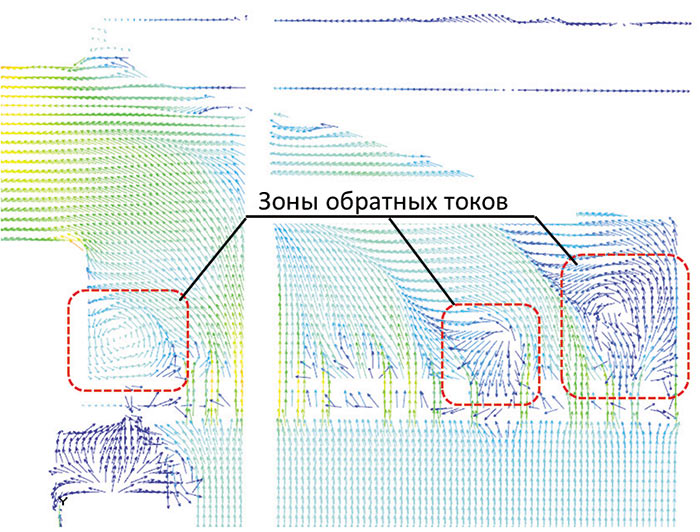
Рис. 11. Вектора скорости в сборной камере реактора
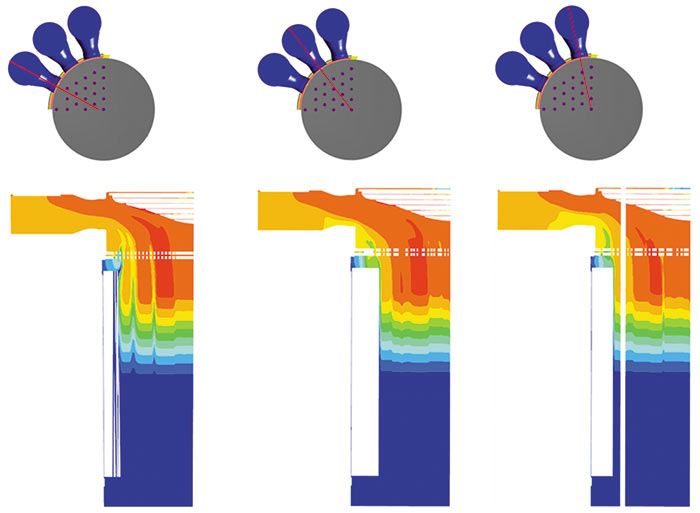
Рис. 12. Распределение температурного поля в вертикальных сечениях реактора, °С
По результатам проведенных исследований было установлено, что в сборной камере реактора наблюдается существенная неравномерность поля скорости с наличием участков обратных токов и застойных зон. Данные области расположены главным образом под центральной частью вытеснителя и на периферийном участке верхней опорной решетки (рис. 11). При этом на разных мощностях работы реактора структура течения остается постоянной. На выходе из АЗ температурное поле имеет ярко выраженный зональный характер, верхняя опорная решетка не дает значимого перемешивания температуры, несмотря на существующую скоростную неравномерность. Значение температуры над опорной решеткой полностью определяется величиной и характером энерговыделения в АЗ. Рис. 12 иллюстрирует распределение температурного поля в вертикальных сечениях реактора. Важно отметить, что благодаря полученным данным на этапе проектирования можно определить проблемные места и оценить их работоспособность, передав результаты расчетов прочнистам.
Кроме того, был выполнен динамический замер температуры в определенных точках сборной камеры, позволяющий определить нагрев теплоносителя и оценить его неравномерность. Было получено значение среднерасходной и средней температуры в горизонтальных сечениях реактора, а также значения среднерасходных температур в местах установки термопар (рис. 13).
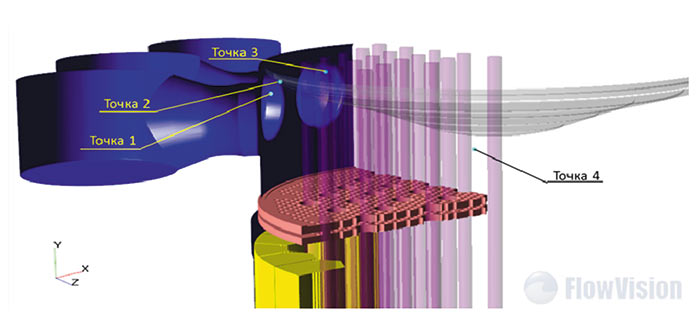
Рис. 13. Расположение точек съема температуры (термопар)
в расчетной области
Таким образом, на примере моделирования течения теплоносителя в первом контуре ядерного реактора показана методика расчета больших и, на первый взгляд, сложных задач, что особенно актуально на этапе проектирования новых конструкций. Основная идея методики заключается в декомпозиции задачи на части с упрощением расчета, без потери точности решения, за счет использования многообразного функционала FlowVision, с последующим итерационным расчетом всех получившихся частей одной большой задачи.
В заключение можно сказать, что применение современных инструментов математического моделирования позволяет оценить работоспособность конструкции на ранних стадиях проектирования и отбросить все заведомо непригодные конструкторские и технологические решения. Это дает возможность избежать проведения лишних дорогостоящих экспериментальных работ.


