Оценка обтекаемости овалоидов и овалоидоподобных тел вращения

Виктор Чебыкин

В статье приводится метод приблизительной оценки обтекаемости овалоидов и овалоидоподобных тел вращения. Обтекаемость различных форм определяется по лобовому сопротивлению давления.

Введение

Продолжая изучение циклоидального овала (циклопа), описанного в статьях [1] и [2], было интересно оценить аэродинамические (гидродинамические) качества его формы. Учитывая то, что состоит он из четырех брахистохрон — кривых скорейшего спуска, возникло предположение: не является ли его форма оптимальной с точки зрения аэродинамики? Оказалось, что не является. Когда это выяснилось, можно было закрыть тему и поставить точку — не все коту (циклопу) масленица, но помешал этому возникший вопрос: а какие же геометрические формы аэродинамически оптимальны? Другими словами — какие из них являются самыми обтекаемыми? На память приходили эллипсоиды и каплеобразные формы, якобы самые обтекаемые.

Создание банка кривых

Для сравнения свойств кривых необходимо провести их селекцию, то есть выбрать наиболее подходящие, затем привести их к одному масштабу и соотношению размеров осей. За эталон масштаба и соотношения осей принят циклоидальный овал с радиусом производящей окружности, равным, например, 20 мм. Соотношение его осей, как известно, равно . Всего было построено и внесено в банк более двух десятков кривых — это известные, малоизвестные и совсем неизвестные кривые. Какова геометрия последних — тема отдельного описания, на котором останавливаться пока не будем.

Создание 3D­моделей

Для придания более стремительной формы отмасштабируем все отобранные кривые до соотношения осей, равного 2p, и операцией вращения создадим 3D­модели овалоидов и овалоидоподобных тел вращения. Часть их показана на рис. 1.

Рис. 1. Овалоиды и овалоидоподобные тела вращения

Для проверки аэродинамических характеристик исследуемой кривых неплохо было бы иметь соответствующую трубу и изготовить модели тел вращения. Второй вариант — воспользоваться расчетным модулем, имитирующим аэродинамическую трубу.

Поскольку ни того, ни другого у нас нет, ограничимся расчетом лобового сопротивления давления.

Расчет лобового сопротивления давления и коэффициентов лобового сопротивления давления (Клсд)

Это сопротивление будем определять по участкам, на которые разобьем исследуемые тела. При этом не учитываем сопротивление трения и завихрений. Скорость движения и вязкость среды также не учитываем, поскольку они одни и те же для исследуемых тел. Значение сопротивления определяем по формуле:

, (1)

где: S — проекция боковой поверхности участка тела вращения на плоскость, перпендикулярную направлению движения;

q — давление среды на единицу площади в плоскости, перпендикулярной направлению движения, для упрощения расчетов принимаем равным 1;

α — средний угол падения потока по участку.

Полное лобовое сопротивление давления тела получаем, суммируя сопротивление отдельных его участков. На рис. 2 показаны графики распределения сопротивления давления по участкам некоторых овалоидов и тел вращения. Следует обратить внимание на большое различие графиков, несмотря на кажущуюся схожесть соответствующих тел (см. рис. 1).

Коэффициенты лобового сопротивления давления определяем как отношение лобового сопротивления давления тела к лобовому сопротивлению давления прямого кругового цилиндра диаметром, равным диаметру миделя тела. В приведенной таблице показаны значения коэффициентов Клсд некоторых овалоидов и тел вращения с соотношением осей, равным 2p (имена кривых: Смерч, Торнадо, Циклоп, Буря, Цикада, Цик­лон — предложены автором и к метеорологии и зоологии отношения не имеют. — Прим. авт. ).

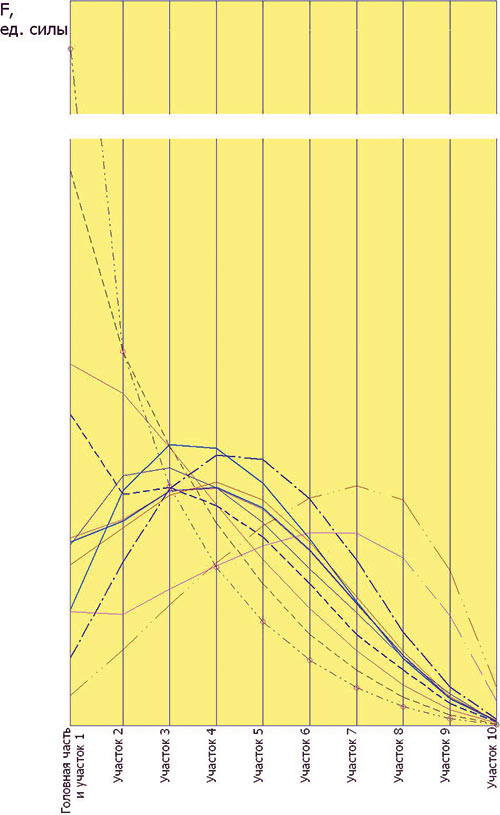
Рис. 2. Лобовое сопротивление давления тел вращения

Коэффициенты Клсд

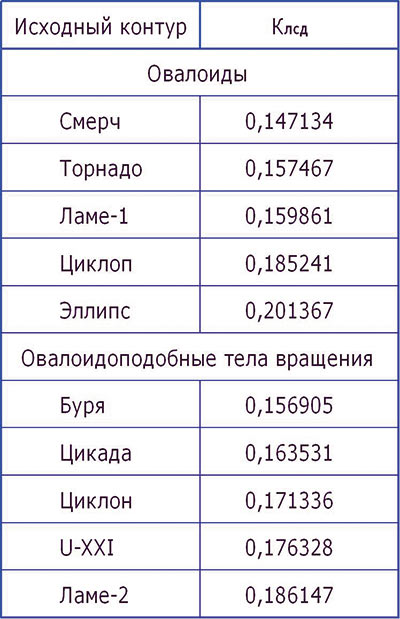
Наименьшим коэффициентом в своих группах обладают Смерч и Буря, однако из­за большой кривизны в районе миделя применение их на больших скоростях будет приводить к срыву потока и завихрениям, что повысит общее лобовое сопротивление. Для малых скоростей они оптимальны. Для высоких скоростей подойдут кривые, находящиеся в линейках Смерч — Торнадо и Буря — Цикада, которые имеют в районе миделя меньшую кривизну. В таблицу эти промежуточные по коэффициенту Клсд кривые не включены, так как их немало. На рис. 1 овалоиды Смерч, Торнадо и тела вращения Буря, Цикада — желтого цвета.

В таблицу также включен Клсд кривой U­XXI. Это не что иное, как контур лобовой части легкого корпуса немецкой подводной лодки U­Boot­Klasse XXI (1943). О высоких гидродинамических качествах лодки говорится в [3]: «Большое внимание было уделено гидродинамическим качествам. Форма корпуса, обеспечивающая малое сопротивление в подводном положении, но, в то же время, позволяющая сохранять и надводные мореходные качества…» Для того чтобы проверить, так ли это, были проведены необходимые измерения, масштабирование и расчеты. Отношение длины лобовой части корпуса к радиусу миделя у нее составляло 3p, а отношение длины хвостовой части к радиусу миделя — 4p, что вполне логично с точки зрения гидродинамики. Тем не менее форма лобовой части выбрана (IMHO) не лучшая. Это выяснилось при масштабировании ее до 2p и расчете лобового сопротивления давления и Клсд (см. таблицу). И это — лучшая лодка 1940­х годов?!

Выводы:

1. Приблизительную оценку обтекаемости тел (не обязательно тел вращения) можно выполнить расчетом их лобового сопротивления давления.
2. Определены наиболее обтекаемые формы овалоидов и овалоидоподобных тел вращения.
3. Определена зависимость обтекаемости овалоидов от при­тупления лобовой части и области миделевого сечения, найдены экстремальные значения параметров притупления (данные в статье не приводятся).
4. Примененная методика позволила проверить гидродинамические качества ранее спроектированного и изготовленного технического объекта. 

Библиографический список:

1. Чебыкин В. Классификация и идентификация эллипсовидных овальных кривых // САПР и графика. 2014. № 3. С. 92­94.
2. Чебыкин В. Циклоидальный и псевдоциклоидальные овалы // САПР и графика. 2014. № 11. С. 105­106.
3. Антонов А.М. Германские электролодки XXI и XXIII серий. Санкт­Петербург. Гангут, 1997. 48 с.

САПР и графика 7`2015