Электротехнические расчеты в APM Structure3D
Весной 2015 года научно-техническим центром «АПМ» выпущена очередная 13-я версия системы APM WinMachine, в которую входит модуль APM Structure3D. Одной из новинок, доступных пользователю при работе с этим модулем, стала возможность проведения расчетов по определению характеристик электромагнитных полей. Данный набор возможностей получил название APM EMA (ElectroMagnet Analysis).
В статье мы познакомим читателей с некоторыми классами задач, которые можно решать с использованием APM EMA, при расчете электротехнических устройств.
Средства анализа электромагнитных полей, реализованные в APM EMA, могут использоваться для исследования различных проявлений электромагнетизма, таких как, например, самоиндукция, плотность магнитного потока, распределение силовых линий магнитного поля, потери электрической мощности и другие родственные явления. Эти средства эффективны при анализе следующих устройств: соленоиды (катушки индуктивности), магнитные пускатели, электродвигатели, источники постоянных магнитных полей, трансформаторы, электромагниты и т.п. APM EMA располагает возможностями для решения проблем микроволновой техники (расчет волноводов, резонаторов и антенн).
Доступны три типа электромагнитного анализа:
- трехмерные стационарные электромагнитные поля;
- трехмерные низкочастотные переменные электромагнитные поля;
- трехмерные высокочастотные электромагнитные поля.
Используемая в APM EMA конечноэлементная формулировка рассматриваемого вида анализа основана на уравнениях Максвелла для электромагнитных полей. Введением скалярного или векторного потенциала в эти уравнения и установлением определяющих соотношений можно получить уравнения, которые удобны для конечноэлементного анализа.
Анализ электромагнитных полей может быть разделен, в зависимости от скорости изменения векторов (индукции и напряженности), характеризующих состояние поля, на низкочастотную (0~1000 Гц) и высокочастотную (~1 МГц~10 ГГц) области.
Практический интерес для расчетов в низкочастотной области представляют задачи, в том числе и стационарные (0 Гц), связанные с электротехническими устройствами, такими как электрические двигатели, электромагнитные актуаторы, трансформаторы и т.п.
При решении задач в высокочастотной области обычно исследуются волновые процессы распространения электромагнитных волн в пространстве или характеристики радиоэлектронных и СВЧустройств, например антенн, резонаторов, волноводов, микрополосковых линий передач и т.п.
В данной статье мы рассмотрим возможности APM EMA, касающиеся стационарного расчета электротехнических устройств лишь в низкочастотной области, в которой можно выделить следующие типы возникающих задач, решаемых с помощью APM EMA:
- электростатика;
- электрокинетика;
- магнитостатика.
Средства APM EMA, используемые для анализа электрического поля, касаются двух областей электрических явлений: протекание постоянного тока (проводники), электростатика (диэлектрики). К типичным параметрам, представляющим интерес, относятся: плотность тока, напряженность электрического поля, распределение напряжений, тепловое действие тока, энергия и силы электрического поля, электростатическая емкость, сила тока и падение напряжения.
В APM EMA могут решаться трехмерные задачи, возникающие при разработке различных устройств, таких как накопительные шины, линии электропередач, высоковольтные изоляторы, экранирующие кожухи, конденсаторы и т.п.
В качестве теоретической основы для анализа стационарного электрического поля в программе используется уравнение Лапласа. Основными неизвестными (узловыми степенями свободы), определяемыми в результате конечноэлементного решения, являются электрические потенциалы (напряжения). По их значениям вычисляются остальные параметры.
Электростатика
Анализ электростатических полей используется для расчета характеристик электрического поля и распределения потенциалов, обусловленных системой электрических зарядов или падением напряжений. Допускается два вида нагрузок: разность потенциалов и плотность зарядов (заряд). Предполагается, что выполняется линейный анализ, то есть параметры, характеризующие электрическое поле, линейно зависят от приложенного напряжения.
Решение состоит в получении величин электрических потенциалов в узлах, что дает возможность найти напряженность и индукцию электрического поля.
Электрокинетика (электрическое поле постоянных токов)
APM EMA можно использовать для нахождения плотности тока и распределения электрических потенциалов (напряжения), возникающих в электрических цепях при протекании постоянного тока или за счет падения напряжения. В качестве входных параметров рассматриваются два вида нагрузок: ток и напряжение. Анализ предполагается линейным, то есть величина электрического напряжения на отдельных участках цепи пропорциональна входному току.
Задача протекания постоянного электрического тока решается с использованием функции потенциала и сводится к вычислению электрических потенциалов в узлах модели, что дает возможность найти напряженность электрического поля и плотность электрического тока.
Статические электромагнитные поля (магнитостатика)
Анализ статического электромагнитного поля возможен для трехмерных задач в линейной постановке. Трехмерная задача магнитостатики является результатом минимизации функционала магнитной энергии, ассоциированного трехмерным вектором потенциала. Имеется возможность моделировать проводники и постоянные магниты в виде источников.
Проводники моделируются конечными элементами или с помощью твердотельных примитивов в виде прямого или кругового стержня и витков катушки. Пользователь имеет возможность моделировать железные сердечники и немагнитные материалы (воздух).
APM EMA предоставляет в распоряжение пользователя линейные магнитные свойства веществ: значения магнитной проницаемости для изотропных и ортотропных материалов. При постпроцессорной обработке результатов имеется возможность получить картину векторного магнитного потенциала, плотность магнитного потока и напряженность магнитного поля.
Особенности интерфейса и работы с новыми типами расчета
Одной из новинок пользовательского интерфейса модуля APM Structure3D при работе с APM EMA являются панели Объекты и Свойства (рис. 1).
Панель Объекты является, по сути, своеобразным деревом документа модуля APM Structure3D, в котором отображаются основные объекты, созданные пользователем, такие как материалы и их свойства, нагрузки (некоторые их виды, характерные для электромагнитных и тепловых расчетов), результаты некоторых типов расчетов, а также ряд вспомогательных объектов. Панель Свойства предоставляет быстрый доступ к свойствам выделенного узла дерева на панели Объекты. С помощью данного интерфейсного нововведения значительно повышается скорость работы пользователя при задании нагрузок на расчетную модель, свойств материалов и просмотре результатов.
Для решения задач электростатики пользователю необходимо определить геометрию расчетной области, используя объемные конечные элементы первого порядка — четырехузловые (тетраэдры), шестиузловые (треугольные призмы) или восьмиузловые (гексаэдры). Для проведения расчета необходимо, чтобы модель не содержала никаких других конечных элементов и была связанной, то есть была единым целым и не содержала отдельно отстоящих узлов.
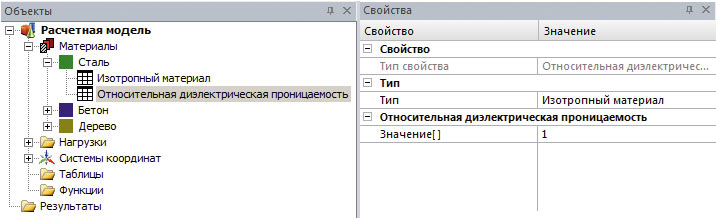
Рис. 1. Общий вид панелей Объекты и Свойства
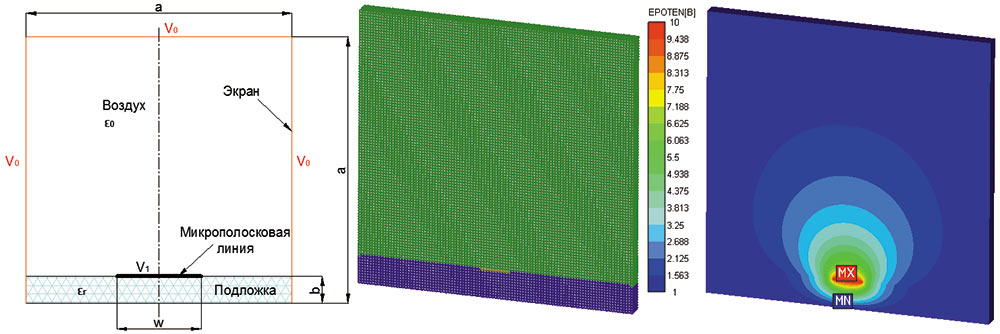
Рис. 2. Расчет электростатического поля вокруг микрополосковой линии
Все материалы, которые задействованы в модели, должны иметь такое свойство, как относительная диэлектрическая проницаемость. Данное свойство материала может обладать ортотропией или быть изотропным, а также зависеть от пространственных координат.
На рис. 2 представлены расчетная схема, конечноэлементная модель и карта распределения электрического потенциала для электропроводящей дорожки (микрополосковой линии передачи), находящейся на диэлектрической подложке в воздухе и экранированной стальным корпусом.
При решении задачи считались заданными значения электрического потенциала на микрополосковой линии и экране, а также диэлектрических проницаемостей материалов. На рис. 3 и 4 представлены результаты расчета напряженности и индукции электрического поля для данной задачи.
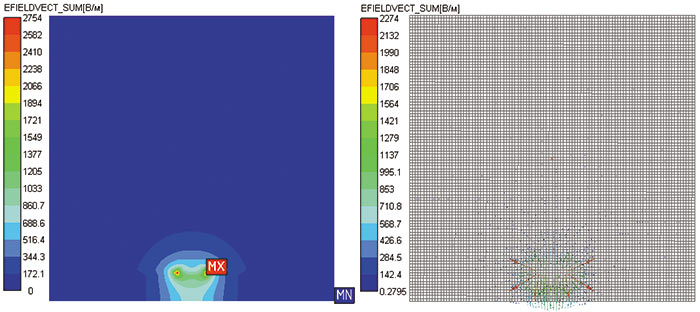
Рис. 3. Карты напряженности электрического поля:
а — контурная; б — векторная
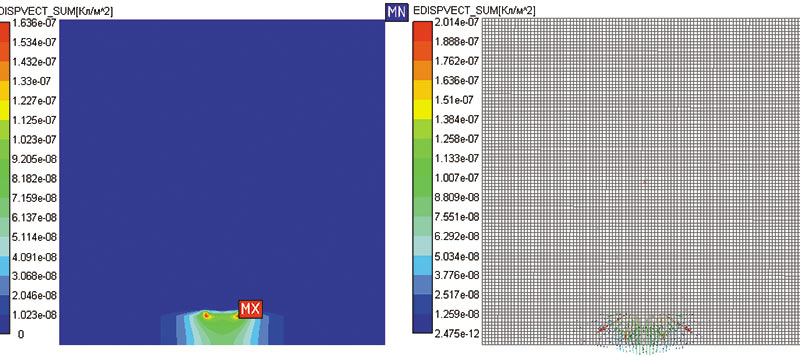
Рис. 4. Карты индукции электрического поля:
а — контурная; б — векторная
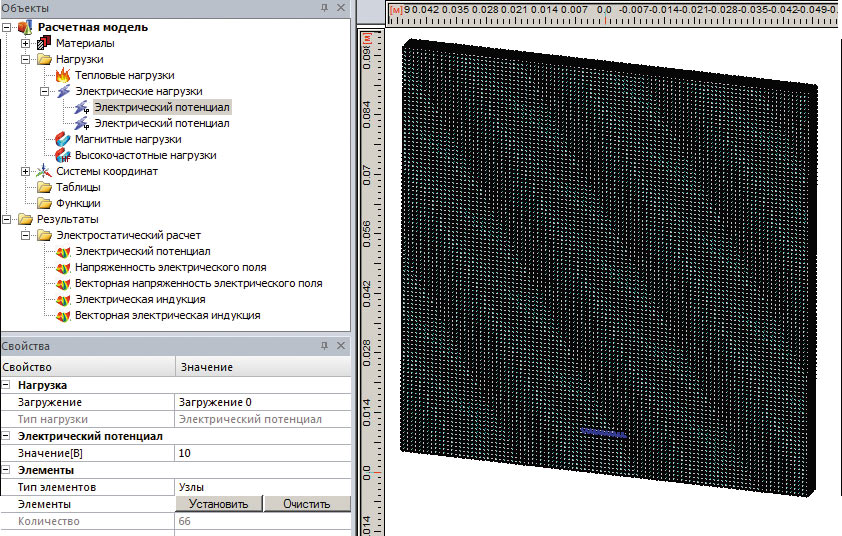
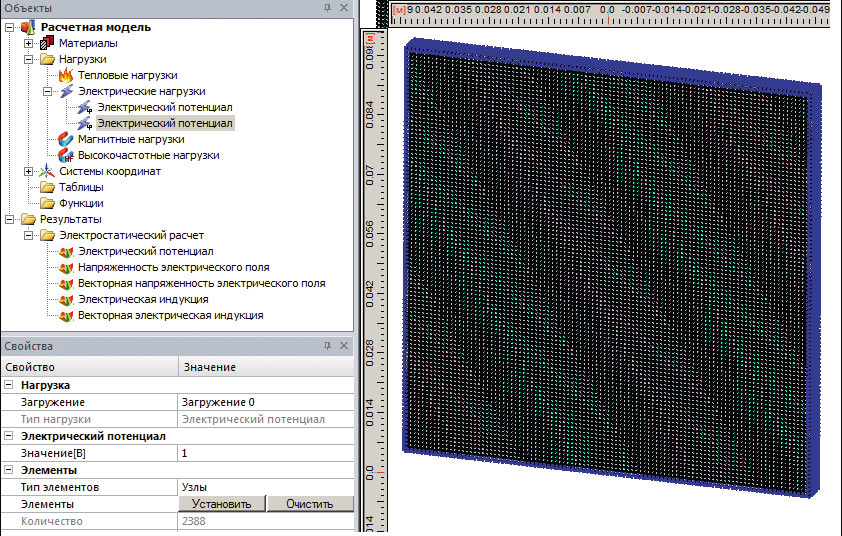
Для задания нагрузок на расчетной модели пользователю нужно воспользоваться функционалом панелей Объекты и Свойства, о которых упоминалось выше. Так, для создания какойлибо электрической или магнитной нагрузки нужно выбрать соответствующий пункт контекстного меню одного из двух узлов дерева (Электрические нагрузки или Магнитные нагрузки), после чего нагрузка появится в дереве проекта. Затем пользователь с помощью панели Свойства должен описать нагрузку (задать значение, выбрать элементы, к которым она прикладывается, и т.п.). При дальнейшей работе после выделения узла нагрузки в дереве проекта элементы, к которым она приложена, подсветятся в рабочей области определенным (выбранным пользователем) цветом (рис. 5).
 a
a
 b
b
Рис. 5. Элементы пользовательского интерфейса для задания нагрузок: а — микрополосковая линия; б — экран
Для просмотра результатов электромагнитных расчетов пользователю также нужно воспользоваться функционалом панелей Объекты и Свойства. Так, после проведения электростатического расчета в дереве панели Объекты появится новый узел Электростатический расчет с группой дочерних узлов (рис. 6), каждый из которых соответствует определенному типу карты результатов. При выборе в дереве определенной карты результатов она будет открыта в новом окне, а на панели Свойства отобразятся элементы пользовательского интерфейса для различных настроек карты (рис. 6).
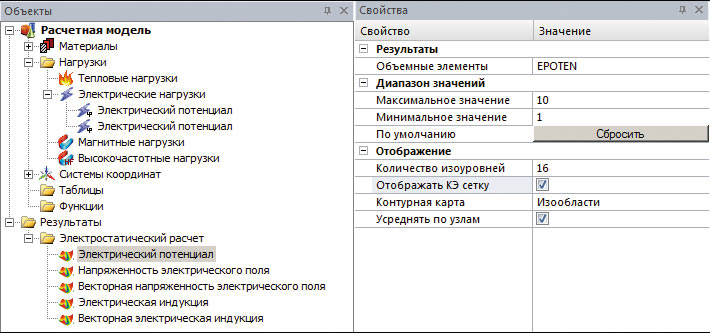
Рис. 6. Элементы пользовательского интерфейса
для просмотра результатов
При решении задачи расчета поля постоянных токов считается, что все объекты стационарные (не изменяемые во времени), токи в проводниках скомпенсированы (то есть сумма всех внешних токов равна нулю). Диэлектрики не могут быть рассчитаны в данном виде расчета — этот вид анализа возможен только для проводников. Неизвестная величина расчета — это электрический скалярный потенциал, через который вычисляются напряженность электрического поля и плотность электрического тока.
Для решения задач расчета поля постоянных токов пользователю необходимо определить геометрию расчетной области, применяя объемные конечные элементы первого порядка. Для проведения расчета необходимо, чтобы модель не содержала никаких других конечных элементов и была связанной, то есть была единым целым и не содержала отдельно отстоящих узлов.
Все материалы, которые задействованы в модели, должны иметь такое свойство, как удельная электрическая проводимость. Данное свойство материала может обладать ортотропией или быть изотропным, а также зависеть от пространственных координат.
Для моделирования задач расчета поля постоянных токов пользователю доступны следующие виды нагрузок и граничных условий: электрический ток; электрический потенциал.
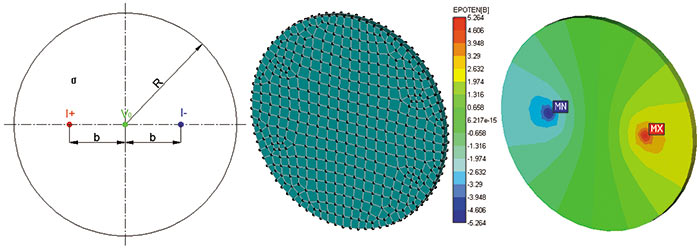
Рис. 7. Расчет электростатического поля электропроводящей пластины
На рис. 7 представлены расчетная схема, конечноэлементная модель и карта распределения электрического потенциала для электропроводящей круглой пластины.
При решении задачи считались заданными значения электрического потенциала в центре пластины (заземление), токи на электродах, а также удельная электрическая проводимость материала. На рис. 8 и 9 представлены результаты расчета напряженности электрического поля и плотности электрического тока для данной задачи.
При решении магнитостатической задачи считается, что все объекты стационарные (не изменяемые во времени). Неизвестная величина расчета — это магнитный векторный потенциал, через который вычисляется напряженность и индукция магнитного поля. Для решения задач магнитостатики пользователю необходимо определить геометрию расчетной области, используя объемные конечные элементы первого порядка. Для проведения расчета необходимо, чтобы модель не содержала никаких других конечных элементов и была связанной, то есть была единым целым и не содержала отдельно отстоящих узлов.
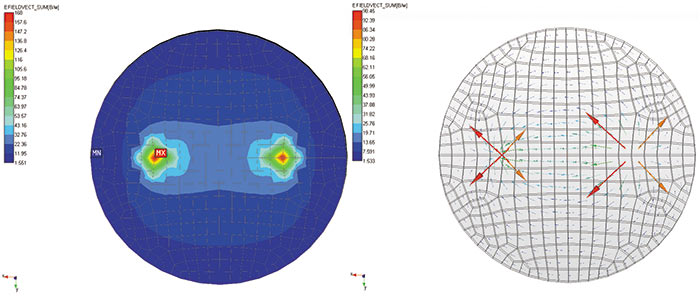
Рис. 8. Карты напряженности электрического поля: а — контурная; б — векторная
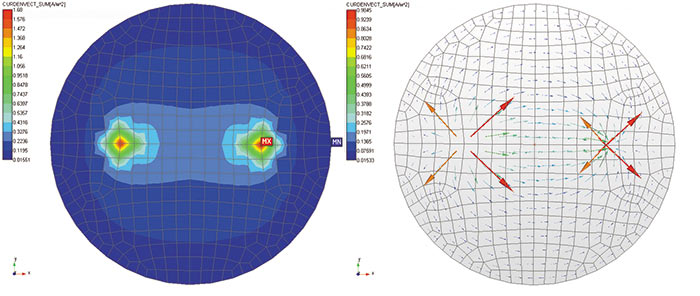
Рис. 9. Карты плотности электрического тока: а — контурная; б — векторная
Все материалы, которые задействованы в модели, должны иметь такое свойство, как относительная магнитная проницаемость. Данное свойство материала может обладать ортотропией или быть изотропным, а также зависеть от пространственных координат.
Для моделирования задач электростатики пользователю доступны следующие виды нагрузок и граничных условий: плотность электрического тока; вектор остаточной намагниченности; векторный магнитный потенциал.
На рис. 10 представлены расчетная схема, конечноэлементная модель и карта распределения векторного магнитного потенциала для магнитопровода с воздушным зазором и постоянным магнитом.
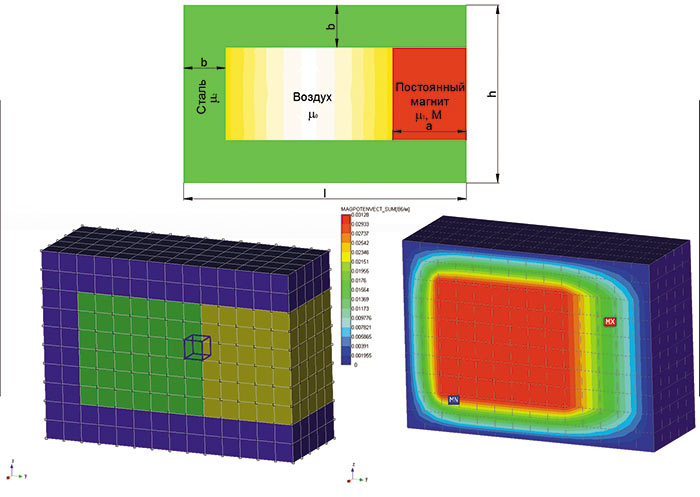
Рис. 10. Расчет магнитного поля магнитопровода
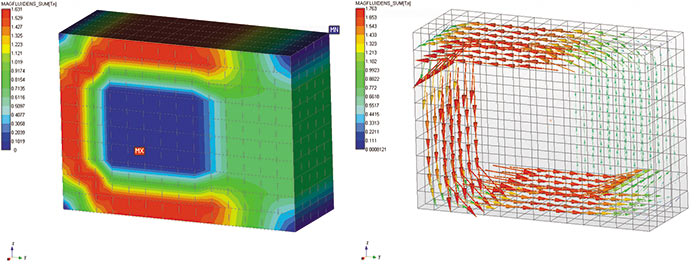
Рис. 11. Карты индукции магнитного поля: а — контурная; б — векторная
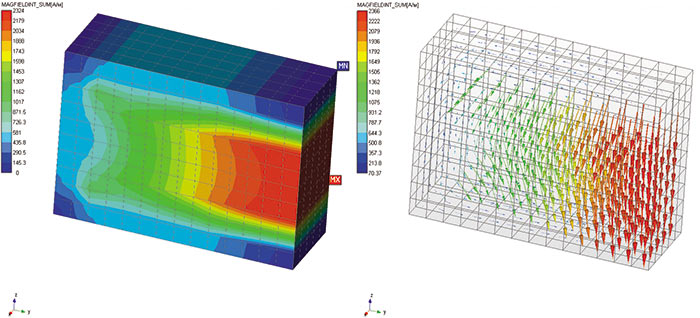
Рис. 12. Карты напряженности магнитного поля:
а — контурная; б — векторная
При решении задачи считались равными нулю значения касательных компонентов векторного магнитного потенциала на внешних гранях расчетной модели, были заданы вектор остаточной намагниченности для постоянного магнита, а также относительные магнитные проницаемости материалов. На рис. 11 и 12 представлены результаты расчета индукции и напряженности магнитного поля для данной задачи.
В целом инструментарий APM EMA, представленный в 13й версии системы APM WinMachine, позволяет покрыть большой спектр прикладных задач в области стационарных расчетов электротехнических устройств. Однако в дальнейшем планируется развитие данного продукта по следующим направлениям:
- нелинейный анализ задач магнитостатики (учет реальных BHкривых для материала);
- развитие возможностей постпроцессорной обработки (расчет интегральных характеристик полей, расчет сил механического взаимодействия между группами конечных элементов, вывод результатов расчета в текстовом виде и т.п.);
- добавление «полубесконечных» конечных элементов для учета моделирования граничных условий на бесконечности при ограниченном числе конечных элементов в модели.
Заканчивая статью, хотелось бы пожелать нашим пользователям, заинтересованным в решении задач по расчету электрических и магнитных полей, успехов в освоении нового инструментария. В свою очередь, коллектив компании НТЦ «АПМ» будет стремиться помочь преодолеть возможные трудности на этом пути.


