Нестационарные электромагнитные расчеты в APM Structure3D

Владимир Шелофаст
Д.т.н., профессор МГТУ им. Н.Э. Баумана, генеральный директор НТЦ «АПМ»
Сергей Майоров
Руководитель отдела мультифизических расчетов НТЦ «АПМ»
Сергей Широков
Ведущий программист НТЦ «АПМ»
Дмитрий Колесников
Программист-аналитик НТЦ «АПМ»

В статье рассмотрены возможности программного модуля APM Structure3D по расчету характеристик нестационарных электромагнитных полей. Приведены базовые сведения, касающиеся теории электромагнитного поля. Представлены результаты расчета характеристик электромагнитного поля для проводника с переменным током и тефлонового резонатора.

В предыдущем номере в статье «Электротехнические расчеты в APM Structure3D» («САПР и графика» № 10'2015, стр. 14­17) мы познакомили читателей с новыми возможностями 13­й версии системы APM WinMachine в области расчета стационарных электромагнитных полей. В данной публикации нам хотелось бы развить тему электромагнитных расчетов в APM EMA (ElectroMagnet Analysis) для нестационарных электромагнитных полей.

Начнем с краткого изложения основных теоретических положений в области классической электродинамики. Как известно, состояние электромагнитного поля описывают уравнения Максвелла, которые могут быть записаны в дифференциальной форме в следующем виде:

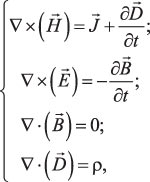
                                (1)

где t — время [с];  — вектор электрической индукции (смещения) [Кл]/[м2];  — вектор напряженности электрического поля [В]/[м];  — вектор магнитной индукции [Тл];  — вектор напряженности магнитного поля [А]/[м];  — вектор плотности электрического тока [А]/[м2]; p — объемная плотность электрического заряда; ∇·()  — операция дивергенции; ∇Ѕ()  — операция ротора.

Векторы, описывающие состояния электромагнитного поля, связаны следующими соотношениями:

(2)

где [e] — матрица абсолютных диэлектрических проницаемостей среды;

, (3)

где [m] — матрица магнитных проницаемостей среды; — вектор собственной остаточной намагниченности постоянного магнита [А/м];

,(4)

где [] — матрица удельных электрических проводимостей среды
1/([Ом]·[м]).

Для описания нестационарного электромагнитного поля свяжем вектора напряженности электрического поля и индукции магнитного поля с электрическим скалярным и магнитным векторным потенциалами следующим образом:

, (5)

где A — векторный магнитный потенциал [Вб]/[м];

, (6)

где j — электрический потенциал [В]; Ñ () — операция градиента.

Для удобства интегрирования по времени мы вводим в рассмотрение интеграл электрического потенциала:

. (7)

Тогда система уравнений Максвелла (1) может быть записана в следующем виде:

для областей с неизвестным распределением плотности тока:

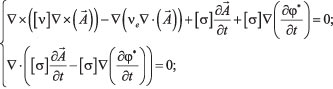(8)

для остальных областей:

,   (9)

где [v] — матрица магнитного сопротивления среды, обратная матрице магнитных проницаемостей среды; ne — среднее магнитное сопротивление среды.

Именно в таком виде уравнения Максвелла решаются в APM EMA при расчете низкочастотных электродинамических переходных процессов.

Рассмотрим возможности APM EMA по расчету нестационарных переходных процессов низкочастотной области на примере определения характеристик электромагнитного поля в прямолинейном проводнике с переменным синусоидальным током.

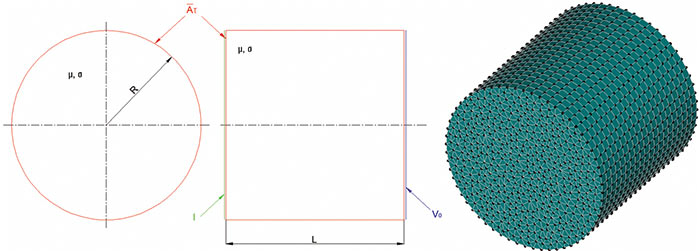
Рис. 1. Расчетная схема и конечно-элементная модель проводника с переменным током

На рис. 1 представлена расчетная схема задачи и конечно­элементная модель, построенная в APM Structure3D, в табл. 1 приведены числовые значения параметров.

После создания конечно­элементной модели необходимо задать два свойства материала: относительную магнитную проницаемость и удельную электрическую проводимость.

Таблица 1. Числовые значения параметров проводника с переменным током

Теперь необходимо задать граничные условия и нагрузки для рассматриваемой задачи. В данном случае рассматривается проводник с неизвестным распределением плотности тока, то есть состояние электромагнитного поля описывается системой уравнений (8). Начнем с описания граничных условий для векторного магнитного потенциала. Поскольку магнитное поле рассматривается в ограниченном пространстве (объеме проводника), то естественным является требование к отсутствию распространения магнитного потока через внешние поверхности, что соответствует равенству нулю на них касательных компонент векторного магнитного потенциала. Поэтому зададим три нагрузки типа Векторный магнитный потенциал, моделирующих данное условие. Сначала зададим нагрузку на цилиндрическую поверхность проводника (рис. 2). Это достаточно легко сделать, выделив все узлы, которые лежат на цилиндрической поверхности (за исключением тех, которые одновременно лежат на торцевых поверхностях), и создав пользовательскую систему координат цилиндрического типа с полярной осью, совпадающей с осью симметрии проводника. Далее задаются компоненты векторного магнитного потенциала на узлы торцевых поверхностей, за исключением тех, которые одновременно лежат на цилиндрической поверхности (рис. 3). На внешних поверхностях остались свободными от нагрузок «реберные узлы», то есть те узлы, которые одновременно принадлежат цилиндрической и торцевым поверхностям. На этих узлах все три компоненты векторного магнитного потенциала должны быть равны нулю (рис. 4), так как касательные компоненты на двух смежных негладких поверхностях образуют полный базис. Данное правило действует для любых моделей при задании внешней изолированной магнитной поверхности в виде векторного магнитного потенциала.

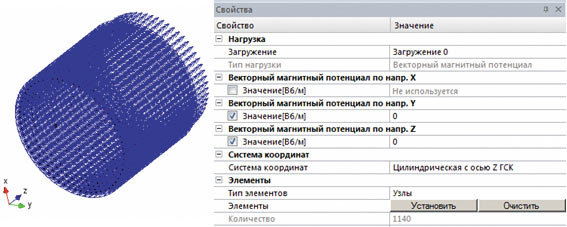
Рис. 2. Векторный магнитный потенциал на цилиндрической поверхности

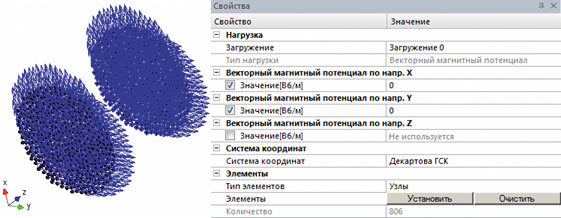
Рис. 3. Векторный магнитный потенциал на торцевых поверхностях

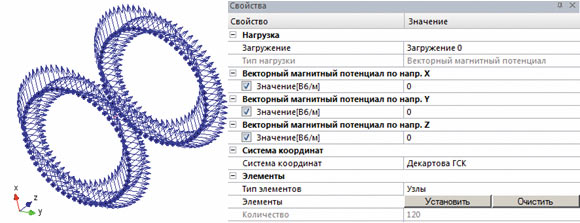
Рис. 4. Векторный магнитный потенциал на реберных узлах

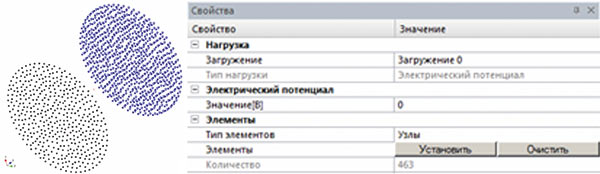
Рис. 5. Электрический потенциал на заземлении

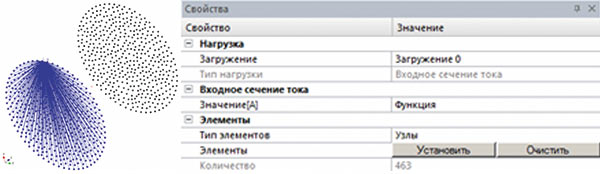
Рис. 6. Входное сечение тока

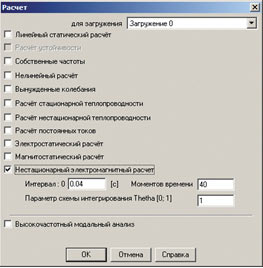
Рис. 7. Настройки нестационарного электромагнитного расчета

Далее перейдем к заданию нагрузок, описывающих электрическое поле. Для моделирования открытого проводника необходимо использовать комбинацию двух различных типов электрической нагрузки на торцах проводника: 1 — электрический потенциал (заземленный конец); 2 — входное сечение тока (сечение, являющееся входным портом для тока). Для задания электрического потенциала необходимо выделить все узлы торцевой поверхности с максимальной координатой Z и на панели Свойства задать значение нагрузки «0» (рис. 5). Как уже упоминалось, задача в области электрического поля решается относительно интеграла по времени от электрического скалярного потенциала, так что пользователь должен иметь в виду, что при проведении нестационарного электромагнитного расчета в низкочастотной области все нагрузки электрического потенциала будут интерпретироваться как интеграл по времени от него.

Для задания входного сечения необходимо выделить все узлы торцевой поверхности с минимальной координатой Z (рис. 6) и на панели Свойства задать значение с помощью инструмента Функция в соответствии со значением тока, приведенным в табл. 1. Отметим, что подобным образом можно моделировать проводники с неизвестным распределением плотности тока практически любой геометрии. Единственное требование — необходимо, чтобы все узлы на входном порту и заземлении лежали в плоскостях, перпендикулярных вектору тока.

Подготовленная модель готова для нестационарного расчета (заметим, что частота синусоидального тока в нагрузке составляет 50 Гц). При расчете необходимо получить два полных цикла, поэтому минимальное время моделирования составляет 0,04 с. Кроме того, следует достаточно точно выбирать шаг интегрирования по времени. В данном случае для описания двух полных волн синусоиды вполне достаточно разбить временной интервал на 40 участков (рис. 7).

В настройках расчета (см. рис. 7) присутствует значение Thetha, которое позволяет пользователю подобрать наиболее экономичный путь для решения конкретной задачи. Параметр схемы интегрирования теоретически [0; 1] определяет однослойный метод интегрирования уравнений по времени. Безусловно, устойчивые схемы соответствуют диапазону [0.5; 1], однако и для них при достаточно большом шаге возможны осцилляции решения. Ниже приведены конкретные методы интегрирования для некоторых значений параметра:

• 0 — метод Эйлера с прямым шагом по времени (с разностью вперед) (классическая схема численного интегрирования дифференциальных уравнений первого порядка);
• 1 — метод Эйлера с обратным шагом по времени (с разностью назад);
• 0,5 — метод Кранка — Николсона (с центральной разностью);
• 2/3 — метод Галеркина.

Отметим также, что при наличии в модели постоянных магнитов и областей с заданной плотностью тока на нескольких первых шагах интегрирования возможно получение осцилляций в решении. Это связано с тем, что задача решается с тривиальными начальными условиями, вследствие чего компоненты электромагнитного поля изменяются скачкообразно.

После проведения расчета в дереве на панели Объекты появится новый узел Нестационарный электромагнитный расчет с группой дочерних узлов (рис. 8), каждый из которых соответствует определенному типу карты результатов. При выборе в дереве определенной карты результатов она будет открыта в новом окне, а на панели Свойства отобразятся элементы пользовательского интерфейса для различных настроек карты (см. рис. 8).

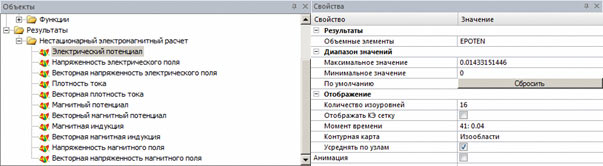
Рис. 8. Элементы пользовательского интерфейса для просмотра результатов нестационарного электромагнитного расчета

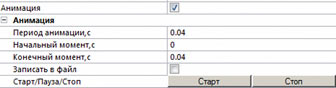
Рис. 9. Элементы пользовательского интерфейса для анимации карт результатов

Отметим, что каждый тип карты результатов может быть анимирован путем выставления переключателя Анимация на панели Свойства (рис. 9).

На рис. 10­12 представлены контурные и векторные карты характеристик электромагнитного поля для различных моментов времени.

Описанный выше анализ применяется в основном для расчета переходных процессов в различных электротехнических устройствах, таких как электрические двигатели, электромагнитные актуаторы, трансформаторы и т.п. В то же время большой практический интерес представляет еще одна область изучения электромагнитного поля — это высокочастотные (во времени) волновые процессы распространения электромагнитных волн в пространстве или характеристики радиоэлектронных и СВЧ­устройств, таких как антенны, резонаторы, волноводы, микрополосковые линии передач и т.п.

Для высокочастотных электродинамических процессов, происходящих по гармоническому закону во временной области, систему уравнений Максвелла (1) можно свести к уравнению Гельмгольца (относительно комплексного вектора напряженности электрического поля [В]/[м]) вида:

, (9)

где [m]r — матрица относительных комплексных магнитных проницаемостей среды[]; «­1» — операция обращения матрицы; j — мнимая единица; w — рабочая угловая частота [рад/с]; [e]r — матрица относительных комплексных диэлектрических проницаемостей среды []; k0 — волновое число вакуума [рад]/[м];  — комплексный вектор плотности тока возбуждения [А]/[м2].

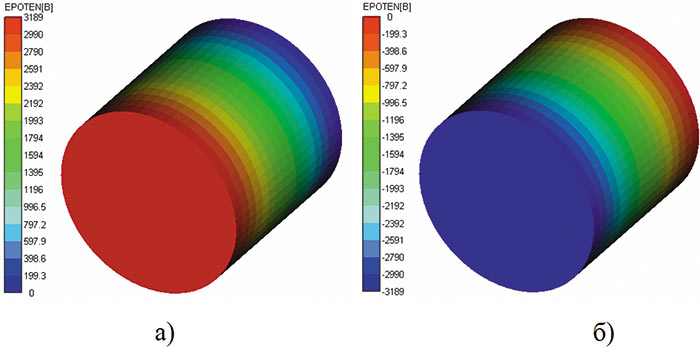
Рис. 10. Карты электрического потенциала: а — 0,005 с; б — 0,015 с

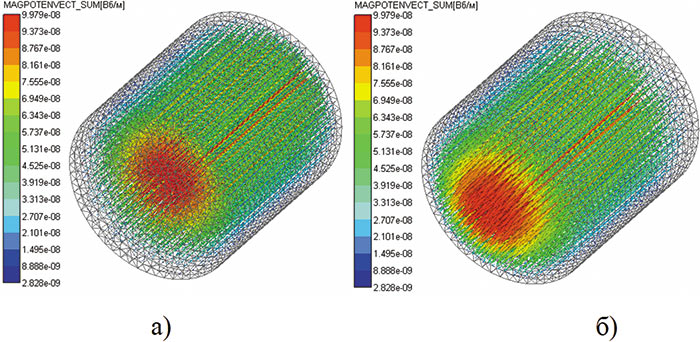
Рис. 11. Карты векторного магнитного потенциала: а — 0,005 с; б — 0,015 с

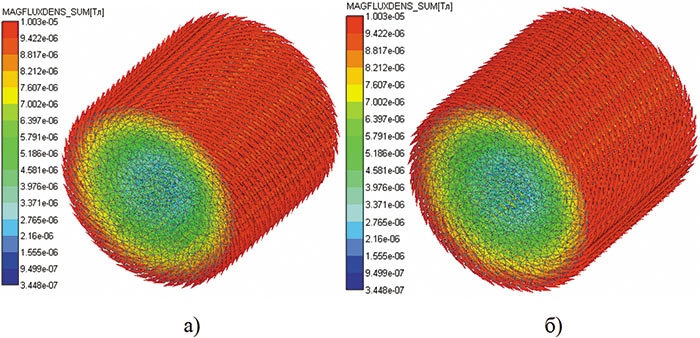
Рис. 12. Карты индукции магнитного поля: а — 0,005 с; б — 0,015 с

Одним из базовых видов анализа на основе уравнения Гельмгольца (9) является высокочастотный модальный анализ, предназначенный для расчета собственных частот (частот среза) и форм электромагнитных структур (волноводы, резонаторы), работающих на высоких частотах (~1 МГц — ~10 ГГц).

В APM EMA при проведении данного типа анализа существует несколько ограничений. Во­первых, так как в любом модальном анализе подразумевается система без внешнего воздействия, то правая часть уравнения (9), тождественно равна нулю. Во­вторых, считается, что волновые процессы не затухают в пространстве, то есть матрицы относительных магнитных и диэлектрических проницаемостей являются действительными. Другими словами, отсутствуют активные сопротивления (диссипация энергии), при этом решение для амплитуд вектора напряженности электрического поля всегда будет действительным.

При решении данного типа задач используется специальный тип объемных конечных элементов — «реберные элементы». С точки зрения пользователя, процесс построения модели ничем не отличается от процесса построения твердотельных конечно­элементных моделей из обычных узловых элементов. Однако нагрузки на модель прикладываются не к узлам, а к ребрам, так как носителями межэлементных связей являются не узлы, а именно ребра, в чем и состоит основное различие. Дело в том, что для обеспечения требуемой точности аппроксимации дискретной модели волновых электромагнитных процессов в качестве неизвестной величины расчета удобно использовать проекцию вектора напряженности электрического поля на «ребра» сетки, через которую затем вычисляется напряженность электрического и магнитного поля.

Рассмотрим возможности APM EMA по расчету собственных частот и форм электромагнитных волн на примере определения характеристик тефлонового резонатора.

На рис. 13 представлена расчетная схема задачи и конечно­элементная модель, построенная в APM Structure3D с использованием команды создания прямоугольного параллелепипеда, в табл. 2 приведены числовые значения параметров.

После создания конечно­элементной модели нужно задать два свойства материала: относительную магнитную проницаемость и относительную диэлектрическую проницаемость.

Единственным граничным условием, возможным в данном виде анализа, является нагрузка типа Идеальный электрический проводник, которая в данной задаче должна быть приложена ко всем внешним ребрам модели (рис. 14).

Нагрузка типа Идеальный электрический проводник, приложенная к ребрам модели, подразумевает равенство нулю проекции вектора напряженности электрического поля на эти ребра, так что фактически данные ребра образуют своеобразную «стену» для распространения электрической волны. Заметим, что если на какой­то внешней поверхности модели не задан Идеальный электрический проводник, то данная поверхность является плоскостью симметрии. Использование этого факта позволит значительно уменьшить размерность сетки для моделей, обладающих геометрической симметрией, а также сократить ресурсы, требуемые для проведения расчета.

Мы описали все подготовительные операции для проведения высокочастотного модального анализа, настройки которого представлены на рис. 15.

После проведения расчета в дереве на панели Объекты появится новый узел 3D­расчет собственных частот электромагнитных с группой дочерних узлов (рис. 16), каждый из которых соответствует определенному типу карты результатов. При выборе в дереве определенной карты результатов она будет открыта в новом окне, а на панели Свойства отобразятся элементы пользовательского интерфейса для различных настроек карты (рис. 16).

Для каждой карты результатов можно на панели Свойства в выпадающем списке Частота просмотреть и выбрать собственную частоту, для которой строится карта (рис. 17).

На рис. 18 и 19 представлены контурные и векторные карты напряженности электромагнитного поля для различных собственных частот.

В заключение хотелось бы отметить, что потребности расчета СВЧ­ устройств не ограничиваются лишь модальным анализом. В настоящее время научно­техническим центром «АПМ» ведутся работы по созданию инструментов, позволяющих производить гармонический анализ СВЧ­структур. Данный тип анализа позволяет исследовать характеристики электромагнитных волн высокой частоты — как вызванных возбудителями, так и отраженных от объектов, а также дает возможность учитывать активные потери в среде распространения и на границах расчетной области. Надеемся, что работы в данном направлении будут полезны и востребованы пользователями. 

САПР и графика 11`2015