Расчет трубопроводной арматуры. Часть I. Преимущества расчета современными методами

Андрей Кавардак
Генеральный директор ООО «ИНТЕРЮНИС»

Михаил Черных
Специалист ООО «ИНТЕРЮНИС»

Алексей Чурилов
Специалист ООО «ИНТЕРЮНИС»

Алексей Журавлев
Специалист ООО «ИНТЕРЮНИС»

Введение

Трубопроводной арматурой (далее — арматура) оснащаются многие установки и агрегаты в химической, нефтедобывающей и нефтеперерабатывающей промышленности, в металлургии и энергетике [1].

При проектировании новой, сертификации импортной или проведении экспертизы промышленной безопасности арматуры необходимо проведение расчетов на прочность для подтверждения ее надежности. Расчеты выполняются в соответствии с требованиями нормативно­технической документации (НТД) — как отечественной, так и иностранной.

Общие положения обеспечения надежности

Причины разрушения арматуры могут быть следующими [2]:

• начальная стадия нарушения целостности корпусных деталей (потение, капельная и газовая течи);
• недопустимое изменение размеров элементов по условиям прочности и функционирования;
• возникновение трещин на основных деталях.

Таким образом, расчет на прочность должен содержать обоснования прочности с оценкой по следующим предельным состояниям:

• разрушение или пластическая деформация по всему сечению детали;
• возникновение макротрещины при циклическом нагружении детали;
• циклическое накопление пластической деформации, которое приводит к недопустимому изменению размеров или квазистатическому разрушению (так называемое прогрессирующее формоизменение);
• недопустимое изменение размеров элементов по условиям функционирования арматуры;
• потеря устойчивости детали.

При этом расчеты можно выполнять как традиционными, так и современными методами.

Традиционные методы расчета

Как правило, большинство подобных объектов рассчитывают по аналитическим формулам, приведенным в соответствующей НТД. Однако такой подход имеет ряд существенных недостатков, поскольку в этом случае вводится ряд упрощений:

• свойства материала принимаются только при расчетной температуре;
• используется линейно­упругая модель поведения материала;
• расчет ведется только для основных элементов (как правило, корпус и шпильки).

В результате не учитывается фактическое распределение температуры в материале, возможность его работы за пределами упругости, а также влияние составляющих элементов арматуры (корпуса, крышки, штока и пр.) друг на друга.

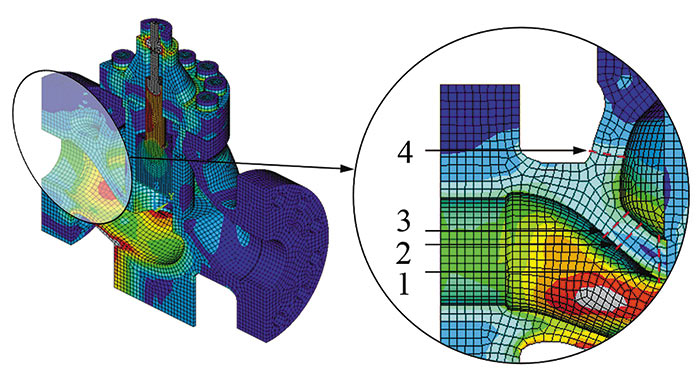
Рис. 1. Различные варианты линий приведения

Поэтому специалисты, проводящие расчет в «ручном» режиме, либо действуют на свой страх и риск, либо закладывают избыточные запасы прочности, что ведет к увеличению металлоемкости конструкции, либо вводят упрощения, которые не отражают реальную работу объекта и вносят значительные погрешности [3].

Для учета всех необходимых факторов, влияющих на работу арматуры, необходимо применение компьютерного моделирования. По результатам расчета с помощью программ конечно­элементного анализа становится возможным определить фактическое распределение напряжений в каждой точке объекта, однако правильная оценка полученных результатов требует определенных знаний и опыта.

Согласно отечественным нормам для оценки прочности арматуры необходимо разделение напряжений по категориям и сравнение полученных значений с допускаемыми. Однако такой подход имеет ряд недостатков. Как правило, большинство деталей арматуры (и в особенности корпус) являются литыми изделиями со сложной геометрией и многочисленными фасонными поверхностями, поэтому при построении геометрических моделей используют объемные элементы. В этом случае для категоризации напряжений необходимо применять линеаризацию, используя линии приведения. Линеаризация позволяет разделить напряжения на мембранные, изгибные и пиковые, но не дает возможности определить, являются ли напряжения местными или общими. Выбор мест и направлений линий приведения, а также их количества является нетривиальной задачей, и какие­либо четкие рекомендации отсутствуют, поэтому данный вопрос остается на совести инженера. В качестве примера на рис. 1 рассмотрен участок арматуры с различными вариантами линий приведения, проведенными в плоскости симметрии.

На рис. 2 приведены результаты линеаризации напряжений вдоль каждой линии приведения.

Рис. 2. Результаты линеаризации напряжений [Па/м]: а — линия приведения 1; б — линия приведения 2;
в — линия приведения 3; г — линия приведения 4
( мембранные / мембранные + изгибные / суммарные напряжения)

Из рис. 2 видно, что даже на таком небольшом участке объекта значения мембранных (12÷50 МПа), мембранных + изгибных (68÷100 МПа) и суммарных (65÷100 МПа) напряжений в зависимости от выбора места линии приведения могут значительно изменяться. Однозначное определение наибольших значений напряжений в каждой категории является чрезвычайно трудоемкой задачей.

Кроме того, элементы арматуры не всегда можно отнести к тонкостенным объектам. В этом случае линеаризация напряжений может дать неконсервативные результаты, так как нелинейное распределение напряжений по толщине стенки недостаточно точно представляется линейным распределением. Более того, погрешность становится гораздо больше, когда материал достигает предела текучести.

Что касается приведенных в отечественной НТД методик расчетов по проверке прочих предельных состояний, то большинство из них малоприменимы для использования в современных программных комплексах.

Современные методы

С интенсивным развитием современных программ конечно­элементного анализа появляются и новые подходы к решению подобных задач. Уже в 2007 году в нормативной документации Американского общества инженеров­механиков (ASME) появились методики, при помощи которых можно достоверно рассчитывать подобные объекты, используя метод конечных элементов.

Расчеты проводятся с помощью метода предельных состояний, в основе которого лежит расчет с дифференцированными коэффициентами запаса для нагрузок и расчетных сопротивлений (Load and Resistance Factor Design). При этом предполагается вероятностный подход, то есть расчетные сопротивления, полученные путем многочисленных испытаний, не должны быть меньше расчетных напряжений в конструкции за весь период эксплуатации. Общий принцип метода представлен на рис. 3 — на графике приведены функции распределения нагрузки S и сопротивления R. Каждая функция имеет свое независимое среднее значение и стандартное отклонение, при этом закон распределения не обязательно может быть нормальным. Функция сопротивления лежит правее функции нагрузки, и существует зона их пересечения. Зона пересечения — это та зона, где нагрузки могут превышать сопротивление и, как следствие, возможно разрушение.

Использование методик, приведенных в [4], обеспечивает возможность проверки достижения всех вышеперечисленных предельных состояний, для чего проводится серия расчетов.

Определение требуемого количества расчетов необходимо начинать с оценки действующих нагрузок и расчетных режимов эксплуатации, так как поверочный расчет для проверки каждого предельного состояния должен проводиться с учетом всех расчетных нагрузок и всех расчетных режимов эксплуатации.

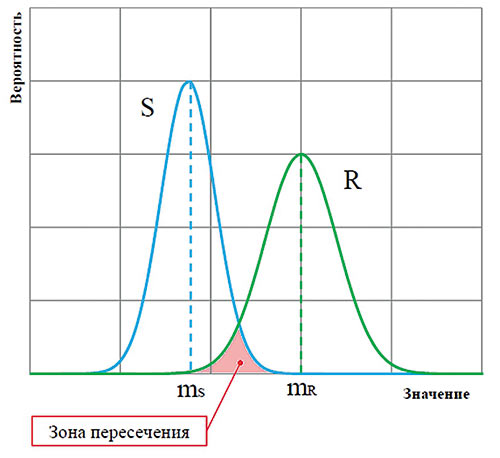
Рис. 3. Пример распределения функций нагрузки и сопротивления

Как правило, арматура может находиться в следующих расчетных режимах: нормальные условия эксплуатации, условия испытаний и нарушение нормальных условий эксплуатации. При этом арматура может испытывать следующие основные нагрузки и воздействия: собственный вес изделия и другого оборудования, для которого данная конструкция служит опорой в установленном состоянии; внутреннее давление; температурные нагрузки; усилия затяжки болтов; сейсмические воздействия и пр.

Если арматура установлена вне помещения, то распределение температуры в материале следует определять для двух вариантов состояния внешней среды — для летнего и зимнего периода.

Стоит отметить, что у арматуры также существует несколько вариантов положения рабочего органа — например, полностью открытый и полностью закрытый, поэтому при расчете необходимо учитывать все расчетные ситуации.

В итоге общее количество требуемых расчетов оказывается достаточно большим (несколько десятков), однако проведение их необходимо, поскольку даже одно неучтенное предельное состояние или нагрузка могут привести к аварии, ущерб от которой может значительно превышать затраты на моделирование.

В следующей статье будет подробно приведена последовательность и даны рекомендации по построению расчетных моделей для расчета современными методами.

Заключение

Таким образом, применение современных методов позволяет повысить точность расчетов, снизить консервативность при оценке результатов и исключить вероятность ошибки.

Преимущества современных методов позволяют перейти на более высокий уровень проведения расчетов, что особенно важно при расчете арматуры, установленной на ответственных объектах. 

Список использованной литературы

1. Гуревич Д.Ф. Конструирование и расчет трубопроводной арматуры.  — Машиностроение, 1968. 888 стр., табл. 159., илл. 540, библ. 20 назв.
2. ГОСТ Р 53672­2009. Арматура трубопроводная. Общие требования безопасности.
3. CAE­CUBE: [Электронный ресурс]. URL: http://cae­cube.ru/ (дата обращения — 08.02.2016).
4. ASME BPVC. Section VIII. Division 2. 2015. Asme Boiler and Pressure Vessel Code AN INTERNATIONAL CODE. VIII Rules for Construction of Pressure Vessels. Division 2 Alternative Rules. 

САПР и графика 3`2016