Расчет трубопроводной арматуры. Часть II. Создание расчетной модели

Андрей Кавардак, Михаил Черных, Алексей Чурилов, Алексей Журавлев

Введение

В данной статье приведена последовательность создания расчетной модели для расчета современными методами, преимущества которых представлены в [1], на примере антипомпажного клапана (далее — арматура). Арматура предназначена для обеспечения нормальной работы компрессора и устранения явления помпажа. Ее основные характеристики отражены в таблице.

Основные характеристики арматуры

Построение геометрии

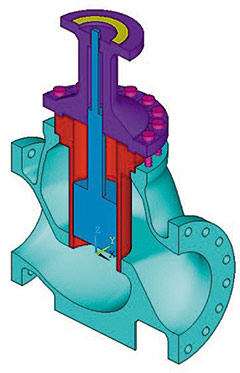
Создание расчетной модели арматуры начинается с построения геометрической модели (рис. 1а). В рассматриваемом примере в качестве программы для моделирования была использована система твердотельного и поверхностного моделирования Autodesk Inventor. Размеры были приняты в соответствии с проектной документацией, причем толщину необходимо задавать с учетом расчетного срока службы и скорости коррозии. Затем геометрическая модель была импортирована в универсальную программную систему конечно­элементного анализа ANSYS (рис. 1б). После задания свойств материалов полученная континуальная модель была разбита на конечные элементы (рис. 1в).

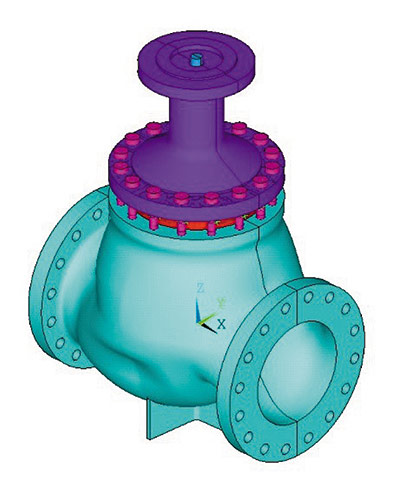
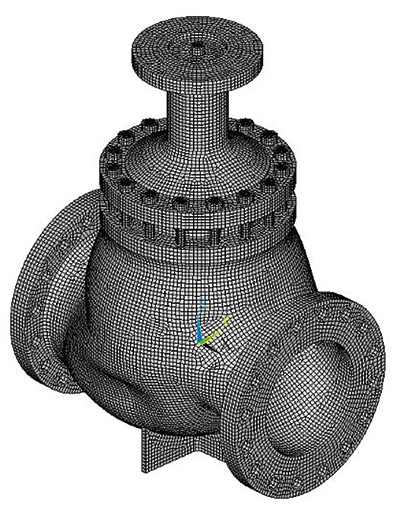
Рис. 1. Модели арматуры: а — геометрическая; б — континуальная; в — конечно-элементная

Определение свойств материала

В зависимости от проверяемого предельного состояния используются различные диаграммы материала: упруго­пластическая, упруго­идеальнопластическая или циклическая.

Все диаграммы материала демонстрируют зависимость напряжения не только от деформации, но и от температуры.

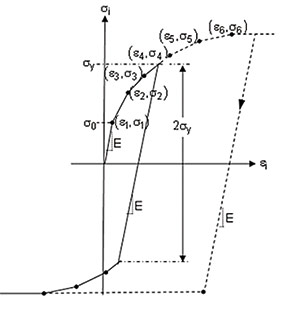
Упруго­пластическая диаграмма строится на основании модели материала Multilinear Isotropic Hardening в ANSYS (рис. 2а).

Диаграмма ограничивается значением истинного напряжения при истинной деформации, после которого начинается идеально­пластический участок. Расчетные значения напряженно­деформационных характеристик принимаются в соответствии с [2], прил. 3­D, п. 3­D.3 (рис. 2б).

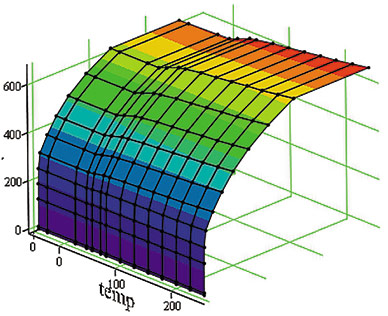ab

Рис. 2. Упруго-пластическая диаграмма материала корпуса арматуры:
а — общий вид; б — определенная в Mathcad

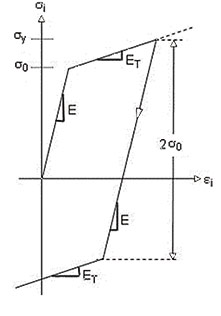
Упруго­идеальнопластическая диаграмма строится на основании модели материала Bilinear Kinematic Hardening в ANSYS (рис. 3а).

Линейные участки моделируют зону упругой работы и площадку текучести материала. Участок пластической работы материала рекомендуется задавать с незначительным упрочнением для обеспечения лучшей сходимости. Расчетные значения напряженно­деформационных характеристик принимаются в соответствии с [3] — рис. 3б.

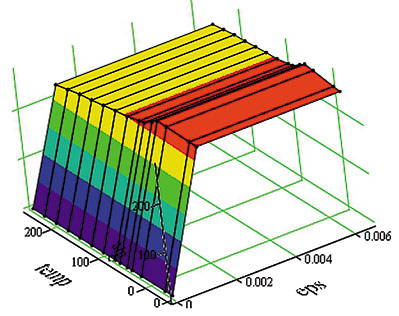ab

Рис. 3. Упруго-идеальнопластическая диаграмма материала корпуса арматуры:
а — общий вид; б — определенная в Mathcad

Данная диаграмма позволяет учитывать кинематическое упрочнение при переменном нагружении (эффект Баушингера).

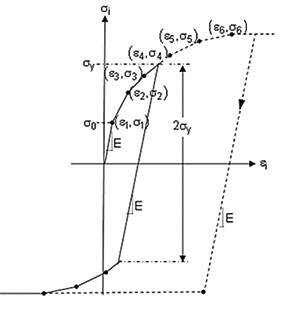
Циклическая диаграмма строится на основании модели материала Multilinear Isotropic Hardening в ANSYS (рис. 4а).

Расчетные значения напряженно­деформационных характеристик принимаются в соответствии с [2], прил. 3­D, п. 3­D.4 (рис.4б).

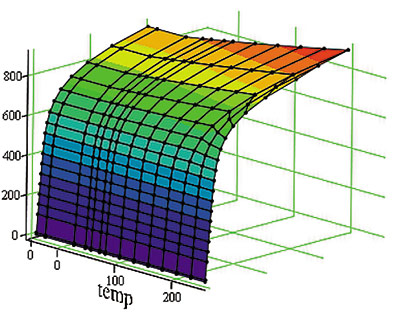ab

Рис. 4. Циклическая диаграмма материала корпуса арматуры:
а — общий вид; б — определенная в Mathcad

Данная диаграмма представляет собой кривую усталости, основанную на испытательных образцах в виде гладкого бруска.

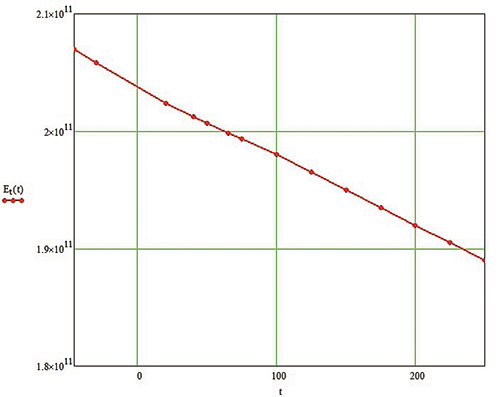
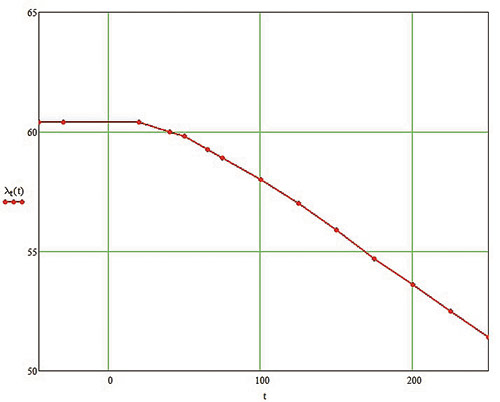
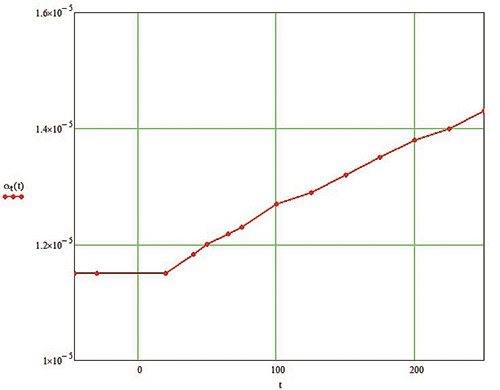
Для автоматического учета влияния температуры на физико­механические свойства материала их рекомендуется задавать зависящими от температуры (рис. 5).

a

b

v

Рис. 5. Графики зависимостей основных физико-механических свойств материала корпуса арматуры от температуры: а — модуль упругости I рода, Па/°C; б — коэффициент теплопроводности, (Вт/м·°C)/ °C; в — коэффициент линейного температурного расширения, (1/°C)/ °C

Моделирование нагрузок и воздействий

Полученной конечно­элементной модели задаются расчетные нагрузки и воздействия. На арматуру действуют собственный вес и вес электропривода, внутреннее давление, температура внутренней и окружающей среды, усилия затяжки шпилек, а также различные ограничения степеней свободы.

Нагрузки от собственного веса учитываются автоматически заданием плотности материалов и ускорения свободного падения. Вес электропривода рекомендуется моделировать распределенной нагрузкой для уменьшения общей вычислительной размерности (рис. 6а).

При моделировании нагрузок от внутреннего давления необходимо обратить внимание на некоторые особенности. Во­первых, в зависимости от положения затвора давление может воздействовать как на всю внутреннюю поверхность, так и только на ее часть, что может быть гораздо опаснее (рис. 6б). Во­вторых, в случае если привод арматуры не имеет независимой опоры, необходимо учитывать передачу давления с затвора на другие элементы арматуры (например, крышку или шпильки).

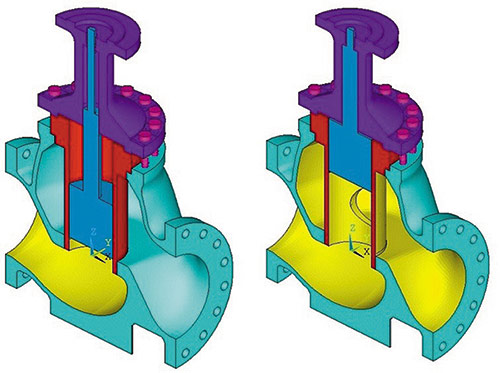ab

Рис. 6. Моделирование нагрузок и воздействий: а — распределенная нагрузка от электропривода;
б — область приложения давления при различном положении затвора

Нагрузки от температурного воздействия моделируются приложением расчетной температуры на соответствующие конечные элементы арматуры и заданием начальной температуры материалов арматуры. В качестве расчетной температуры рекомендуется принимать фактическое конечное распределение температур в материале, для чего требуется провести термодинамические расчеты (рис. 7). За исходную температуру для термодинамического расчета принимается температура внутренней среды при рассматриваемом расчетном режиме и соответствующая температура окружающей среды.

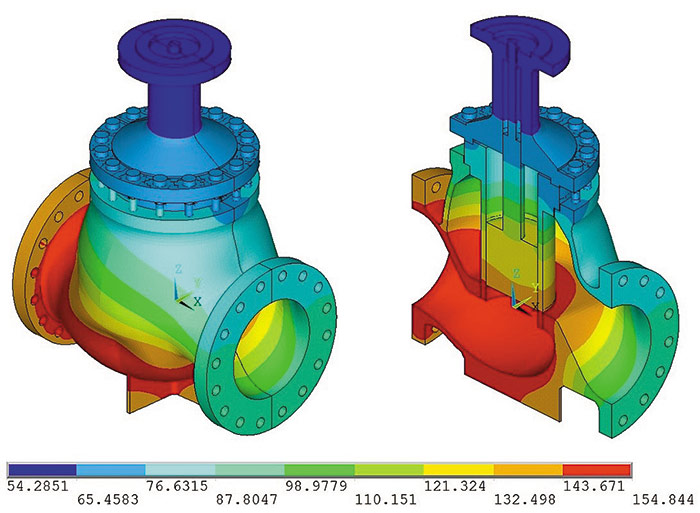
Рис. 7. Карты распределения температуры по результатам термодинамического расчета
для летнего сезона при закрытом затворе, °C

В случае если необходимо учесть температурное воздействие с коэффициентом перегрузки, то рекомендуется вводить данный коэффициент к коэффициенту линейного расширения, что позволит оставить свойства материала неизменными.

Для моделирования предварительного натяжения шпилек от силы затяжки были использованы элементы PRETS179.

Ограничения степеней свободы в данном случае выражаются в виде закреплений (задания условия симметрии, закрепления основания и др.) и контактных взаимодействий элементов. Для моделирования контактных взаимодействий элементов были использованы элементы TARGE170 и CONTA174, причем элементы TARGE рекомендуется делать больше элементов CONTA.

В результате общая вычислительная размерность каждой расчетной модели составила 380 323 узлов и 108 666 элементов.

Заключение

Создание модели для применения современных методов расчета требует определенных навыков и опыта владения различными программными комплексами. Однако в результате становятся возможными следующие действия: моделирование реальной геометрии арматуры; определение фактического распределения температуры по всему объекту, а на основании этого — учет изменения свойств материала; установление взаимного влияния элементов конструкции и пр. Возможность учета разнообразных факторов, влияющих на работу арматуры, позволяет заранее прогнозировать ее работу в различных ситуациях [4]. 

Список использованной литературы

1. Кавардак А., Черных М., Чурилов А., Журавлев А. Расчет трубопроводной арматуры. Часть I. Преимущества расчета современными методами // САПР и графика. 2016. № 3. С. 78­80.
2. ASME BPVC. Section VIII. Division 2. 2015. ASME Boiler and Pressure Vessel Code AN INTERNATIONAL CODE. VIII Rules for Construction of Pressure Vessels. Division 2 Alternative Rules.
3. ASME BPVC. Section II. Part D. 2015. ASME Boiler and Pressure Vessel Code AN INTERNATIONAL CODE. Section II Materials. Part D Properties (Metric).
4. CAE­CUBE: [Электронный ресурс]. URL: http://cae­cube.ru/ (дата обращения — 12.02

САПР и графика 4`2016